Другие классы автоматов

Интересно выделить особые классы автоматов, математические модели которых опираются только на два носителя алгебры.

Пусть |X| = 1. Тогда математическая модель и система рекуррентных соотношений имеют вид:

,

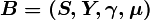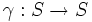
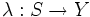
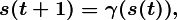
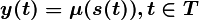
где S и Y — конечные непустые множества состояний и в ы ходных сигналов, а 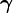и 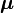— отображения выше указанного вида. Особенностью функционирования такого автомата является генерация последовательности символов выходного слова только в зависимости от последовательности состояний автомата. Такой автомат получил название автономного конечного детерминированного автомата.

Для каждых начального состояния 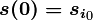и натурального числа t автомат B определяет две последовательности:

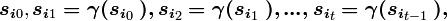
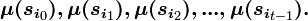
Конечный автомат может быть представлен как преобразователь входных последовательностей в выходные. При этом выходные последовательности могут рассматриваться как порождаемые, а входные — как представляемые. Выходные последовательности автомата определяют множество слов, порождаемых этих автоматом. Автономный КДА называется порождающим, если порождаемое им слово представлено как выходная последовательность, при этом такая последовательность называется порождаемой данным автоматом.