Cинтез функциональной схемы конечного автомата

Задачу синтеза конечного автомата к задаче синтеза комбинационных схем. Вы уже знаете, что структура конечного С-автомата имеет вид:

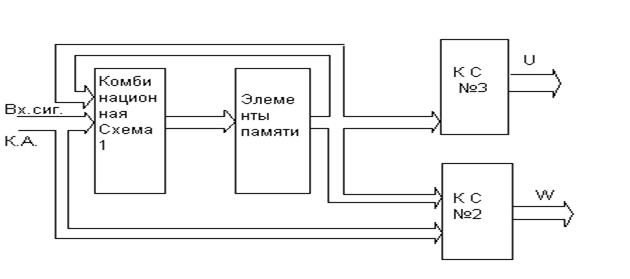
Если синтезировать комбинационные схемы входящие в эту структуру, то можно начертить функциональную схему конечного автомата. Для этого следует определить, сколько входных и выходных проводников в каждой из комбинационных схем. Каждому входному проводнику соответствует аргумент булевой функции, а на каждом выходном проводнике формируется значение булевой функции. Таким образом, число выходных проводников определяет число функций, которое реализует комбинационная схема, а число входных проводников определяет число аргументов, от которых зависят эти функции.

Для определения числа входных шин конечного автомата (они являются частью входов первой и второй комбинационных схем), выходных шин 1-го рода, 2-го рода, числа элементов памяти используют формулу 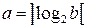, где ] [ -означает округление к большему целому.

1) количество входных проводников конечного автомата:

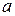- число входных шин,

-число входных сигналов конечного автомата (число элементов в множестве 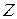, т.е. мощность множества ).

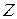2) число выходных шин 1-го рода (число выходных проводников комбинационной схемы 2):

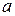- число выходных шин 1-го рода,

- мощность множества .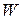

3) число выходных шин 2-го рода (число выходов комбинационной схемы 3):

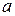- число выходных шин 2-го рода,

- число выходных сигналов 2-го рода абстрактного автомата (мощность множества ).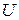

4) число элементов памяти:

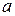- число элементов памяти,

- число состояний автомата (мощность множества ).

После этих вычислений производится кодирование входных, выходных сигналов и состояний автомата. При этом каждому символу входящему в множества 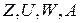ставится в соответствие кодовая комбинация на соответствующих входных, выходных шинах а также на элементах памяти.

Замечание. На практике в ряде случаев коды входных и выходных сигналов задаются заказчиком.

Пример. Синтезируем С – автомат, заданный таблицей переходов и таблицей выходов. Будем использовать логические элементы булевого базиса, уравнения представляем в дизъюнктивных формах, а в качестве элементов памяти используем Т – триггеры.

Таблица переходов – выходов автомата:

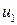
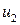
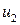
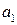
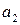
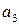
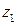
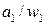
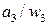
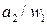
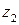
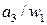
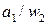
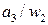
Множество 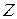содержит два элемента, поэтому комбинационная схема 1 автомата имеет один входной проводник. Пусть 0 на этом проводнике соответствует 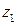, а единица - .

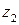Автомат имеет 3 состояния, следовательно, нужны 2 триггера (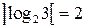). Состояние конечного автомата определяет состояние этих триггеров. Примем, что если первый триггер находится в нуле, а второй триггер в единице, то это будет состояние 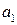(Говорят, что состоянию 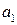приписан код 01). Продолжаем кодирование состояний. Припишем состоянию 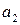код 10, а состоянию 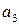код 00.

Замечание 1. Естественно, что проектировщик может выбрать для кодирования состояний и другие коды.

Замечание 2. От выбранных кодов зависит сложность комбинационной схемы 1.

У автомата три типа выходных сигналов 1-го рода, следовательно, он имеет 2 выходных проводника 1-го рода. Пусть сигналы 00 на этих проводниках соответствуют 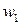; 01 –соответствуют 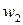; 10 – .

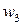Комбинационная схема 3 имеет один выходной проводник. Пусть 0 на этом проводнике соответствует сигналу 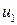, а 1 – сигналу .

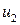Теперь нужно заменить символы 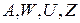в абстрактной таблице переходов–выходов на соответствующие коды и получить кодированную таблицу переходов-выходов:

Используя две верхние строки кодированной таблицы переходов-выходов, синтезируем схему формирования сигналов 2-го рода (на рисунке это комбинационная схема 3).

Обозначим состояния триггеров автомата _.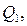

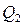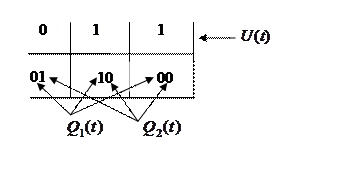
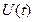- это выходной сигнал (значения функции);

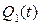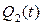, - это состояния триггеров автомата (аргументы функции).

Таким образом эти строчки представляют собой таблицу истинности булевой функции, по которой синтезируется комбинационная схема 3. Можно (при желании) представить эту таблицу в стандартной форме

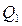
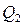
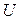
0 1 0

1 0 1

0 0 1

Минимизируем функцию U:

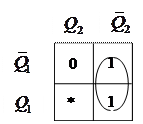
Минимальное выражение: .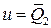

Оставшаяся часть таблицы переходов-выходов содержит информацию для синтеза комбинационной схем 1 и 2. В верхних треугольниках записаны коды состояний, в которые переключается конечный автомат в момент времени , а в нижних – коды на выходных проводниках схемы, формирующей сигналы 1-го рода (комбинационная схема 2. Перепишем эту таблицу, оставив в ней только нижние треугольники. Теперь эта таблица является таблицей истинности, по которой строится комбинационная схема 2:

Обозначим сигналы на выходных проводниках 1-го рода 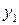и 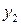и перепишем эту таблицу:

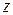
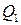
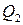
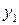
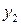
Минимизируем функци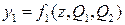и и :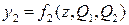

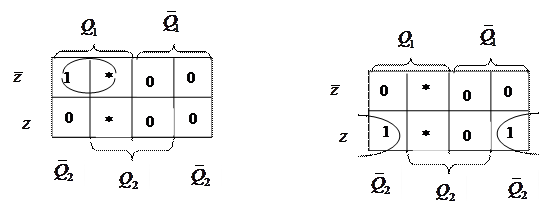
Минимальные выражения: ,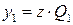

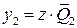
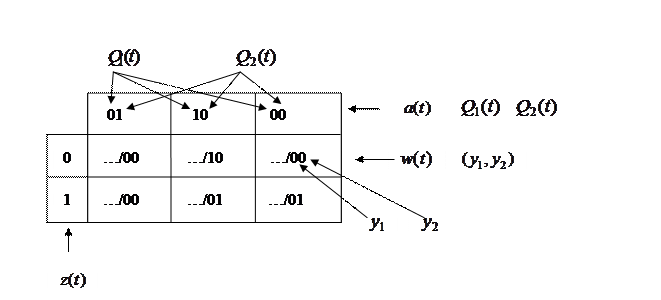
Теперь нужно синтезировать схему, переключающую Т – триггеры. Необходимая для синтеза информация берется из кодированной таблицы переходов-выходов и таблицы функционирования Т триггера. Используя эти таблицы, заполняют так называемую таблицу функций возбуждения элементов памяти. (Под функциями возбуждения понимают функции, описывающие управляющие входы триггеров).

Рассмотрим таблицу переходов-выходов, обращая внимание только на верхние треугольники:

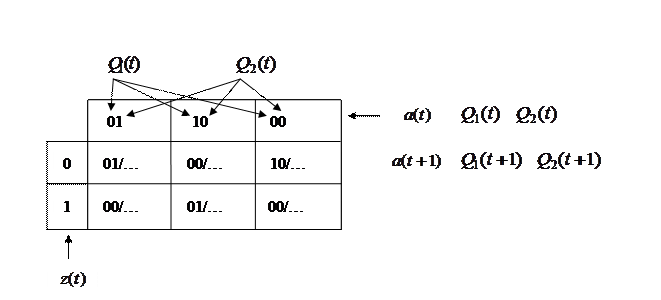
При построении таблицы функций возбуждения элементов памяти рисуют следующую таблицу:

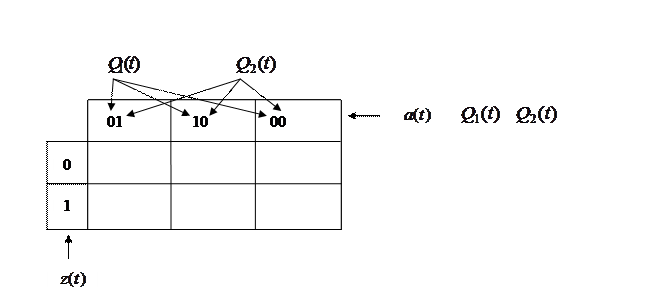
Верхняя строка этой таблицы – состояния конечного автомата, левый столбец – входные сигналы автомата. В пустые клетки нужно вписать сигналы, которые необходимо подать на управляющие входы триггеров, чтобы обеспечить переключение автомата, соответствующее таблице переходов.

Рассмотрим, например, заполнение клеточки для случая, когда автомат находится в состоянии 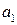(код 01), а на вход приходит сигнал 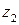(код 1). Согласно таблице переходов автомат должен переключиться в состояние 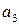(код 00). Следовательно, первый триггер должен переключиться из 0 в 0, а второй триггер – из 0 в 1. Вспомните принцип работы Т-триггера: если на управляющий вход V подать 0, то триггер останется в том же состоянии, если же на вход V подать 1, то после прихода синхросигнала триггер переключится в противоположное состояние. Понятно, что для обеспечения требуемого переключения автомата на вход V первого триггера нужно подать 0, а на вход V второго триггера подать 1.

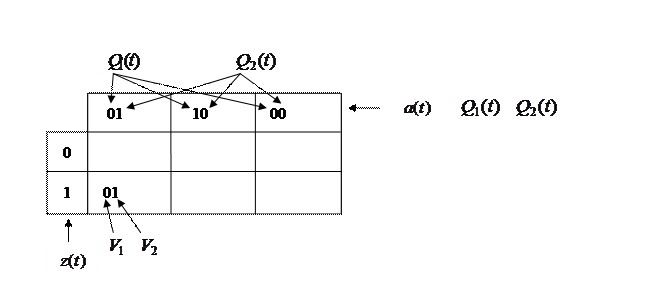
После заполнения таблица функций возбуждения элементов памяти имеет вид:

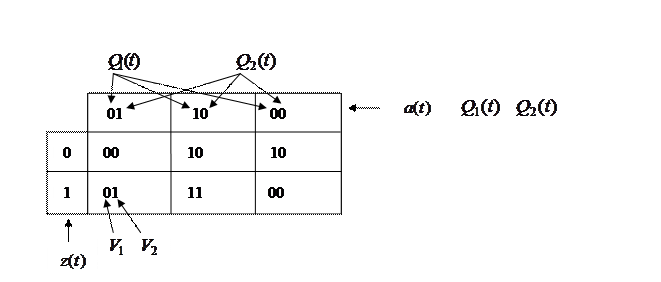
Эта таблица является таблица истинности комбинационной схемы 1.

Запишем эту же таблицу в привычном виде:

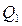
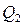
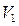
Минимизируем функци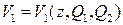и и :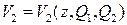

Таблица для V₁ Таблица для V₂

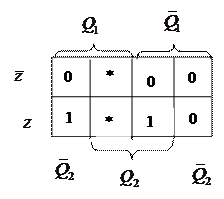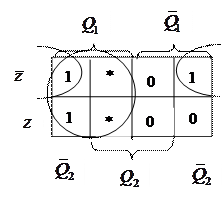Минимизированные функци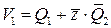и: и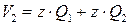

Зная структурную схему конечного автомата, по полученным уравнениям чертят функциональную схему конечного автомата.

Минимизация полностью определенных автоматов.

Определение. Два состояния автомата 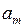и 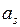называются эквивалентными, если реакция автомата, находящегося в состоянии 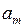совпадает с реакцией конечного автомата, находящегося в состоянии 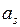для слов произвольной длины.

Для минимизации числа состояний следует получить разбиение множества состояний конечного автомата на непересекающиеся подмножества эквивалентных состояний (классы эквивалентности). Если в каждом подмножестве оставить только одно состояние, то получится автомат с минимальным числом состояний.

Определение. Два состояния автомата 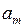и 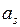называются k - эквивалентными, если реакция автомата, находящегося в состоянии 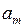совпадает с реакцией конечного автомата, находящегося в состоянии 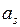для слов длины k.

Алгоритм минимизации числа состояний:

Шаг 1. Находятся последовательные разбиения 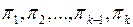множества состояний автомата на классы одно -, двух -, …, 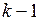-, - 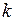эквивалентных состояний. Шаг выполняется до тех пор, пока в каждом классе окажется только по одному состоянию, либо когда текущее разбиение не совпадет с предыдущим разбиением: 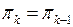. Нетрудно убедиться, что последующие разбиения будут также совпадать с 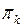, т.е. полученные 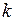- эквивалентные состояния являются просто эквивалентными.

Шаг 2. В каждом классе разбиения 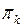оставляют по одному состоянию.

Шаг 3. В таблице переходов – выходов вычеркивают столбцы, соответствующие удаленным состояниям. Если в оставшихся столбцах имеются символы удаленных состояний, то они заменяются на не удаленные эквивалентные им состояния.

Шаг 4. В качестве начального состояния выбирается любое состояние эквивалентное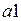

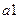
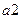
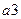
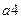
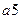
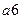
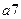
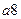
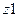
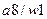
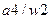
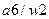
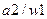
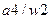
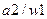
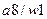
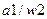
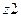
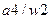
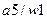
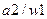
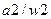
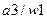
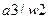
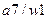
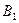
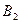
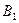
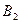
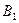
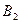
Получено разбиение 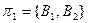на множества одноэквивалентных состояни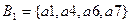й и .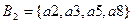

Строим новую таблицу, в верхней строчке которой записываем все состояния автомата, сгруппировав их по множествам одноэквивалентных состояний, в левом столбце записываем все входные сигналы автомата. Для заполнения пустой клетки, стоящей на пересечении строки и столбца 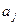по таблице переходов определяем, в какое состояние должен переключиться автомат, но в клетку вписываем не само состояние, а символ множества одноэквивалентных состояний в которое данное состояние входит.

Множество	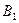Множество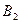

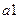
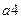
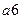
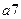
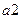
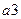
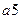
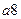
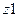
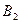
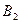
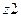
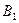
После заполнения таблица будет иметь вид:

Множество	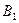Множество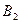

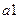
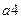
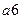
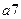
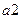
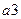
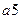
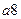
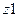
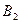
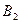
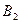
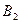
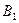
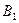
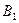
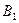
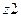
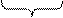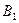
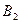
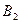
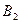
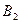
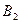
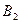
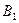
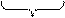
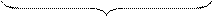
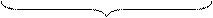
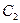
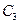
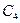
Выделяя одинаковые столбцы для состояний, принадлежащих одному и тому же множеству, получаем разбиение 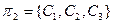, , 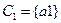, , 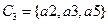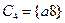. Разбиение 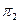определяет множества двухэквивалентных состояний.

Строим таблицу для поиска трех-эквивалентных состояний:

. , , , , .

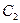
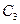
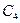
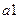
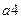
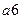
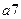
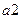
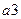
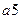
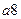
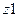
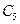
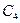
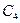
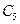
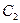
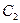
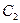
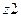
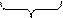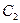
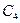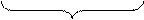
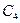
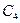
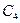
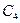
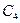
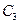
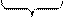
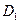
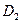
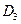
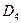
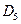
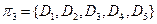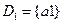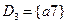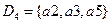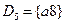Строим таблицу для поиска четырех-эквивалентных состояний:

. , , , , .

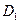
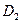
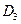
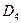
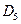
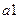
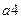
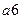
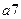
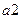
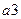
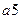
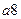
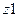
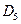
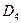
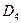
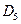
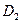
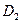
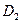
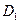
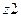
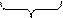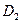
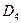
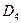
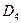
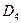
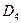
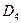
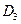
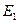
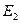
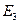
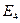
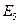
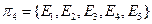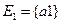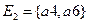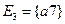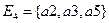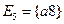Разбиение 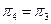, следовательно, найдены эквивалентные состояния. Оставим в каждом множестве эквивалентных состояний по одному состоянию. Для этого удалим из множества 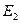состояние 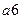, и состояния 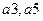из множества 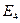. Вычеркиваем столбцы, соответствующие удаленным состояниям из таблицы переходов – выходов:

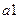
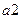
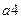
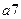
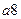
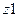
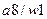
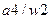
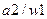
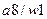
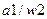
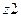
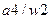
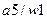
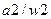
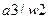
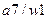
Обратите внимание, что после вычеркивания столбцов в таблице могут остаться символы удаленных состояний (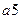 в третьем столбце и 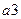в пятом столбце). Естественно, что эти состояния должны быть заменены на эквивалентные им, не удаленные состояния. (В примере состояния 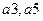заменяются состоянием 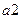). Окончательная таблица переходов – выходов минимального автомата имеет вид:

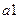
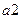
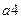
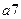
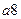
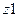
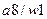
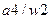
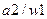
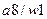
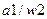
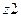
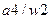
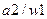
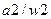
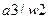
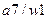
При минимизации автоматов Мура одинаково отмеченные состояния считаются 0 – эквивалентными, а поиск эквивалентных состояний начинается с поиска разбиения .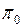

Пример.

, , , .

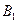
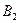
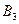
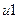
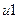
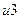
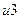
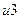
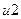
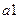
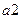
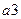
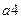
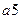
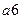
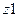
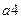
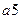
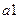
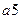
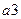
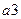
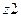
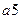
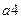
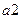
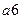
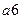
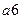
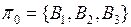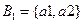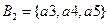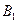
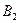
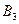
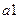
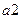
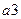
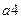
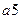
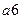
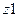
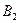
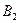
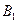
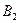
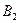
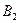
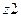
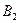
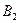
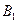
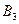
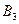
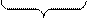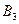
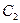
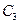
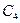
Получено разбиение , , , , .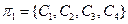

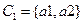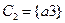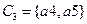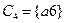Обратите внимание, что состояния 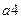, 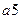и 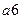отнесены к различным классам , несмотря на то, что их столбцы одинаковы. Причина заключается в том, что эти состояния относятся к разным классам 0 – эквивалентности и поэтому принципиально не могут быть 1 -, 2 -, и т.д. эквивалентными.

, , , , , .

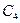
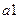
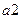
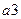
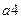
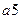
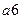
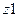
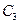
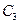
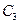
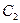
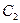
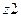
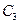
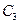
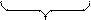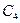
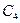
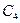
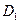
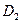
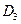
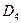
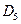
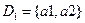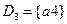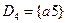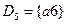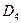
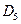
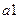
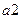
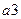
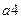
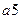
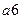
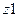
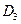
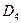
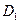
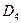
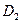
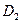
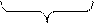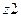
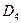
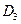
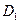
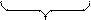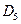
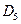
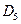
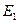
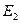
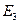
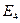
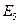
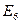
В разбиении 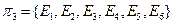каждое множество содержит одно состояние, поэтому минимизация данного автомата прекращена, т.к. в нем нет эквивалентных состояний.