Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства дисперсии
|
|
1. Дисперсия неотрицательна –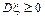 
.
2. Дисперсия постоянной равна нулю:
D(C) = 0. (2.12)
Действительно, D(C) = M(C2) - (M(C))2= C2- C2=0.
3. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D (C× x) = C2× D (x). (2.13)
Действительно,
.
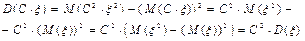4. Дисперсия суммы (разности) конечного числа независимых в совокупности случайных величин равна сумме дисперсий слагаемых:
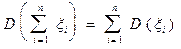. (2.14)
Доказательство проведём для двух слагаемых.
.
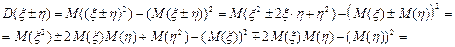
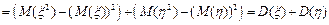Поскольку размерность дисперсии случайной величины равна квадрату размерности самой случайной величины, то в ряде случаев удобнее пользоваться корнем из дисперсии. Эта характеристика имеет ту же размерность, что и сама случайная величина, и её называют среднеквадратическим отклонением
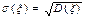. (2.15)
Отметим, что для четвертого распределения, где все значения находились на расстоянии 2 от среднего, s = 2.
Из свойств дисперсии немедленно следуют свойства среднеквадратического отклонения: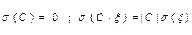 
.