Примеры. 1) Пространство Rn . Элементами этого пространства являются n-ки чисел ( а1, а2 , , аn ), сложение и умножение на число производится покомпонентно

1) Пространство Rⁿ. Элементами этого пространства являются n-ки чисел (а₁, а₂, …, а_n ), сложение и умножение на число производится покомпонентно, аналогично операциям с векторами на плоскости (R² ) и в пространстве (R³ ).

2) Множество всех функций f(x), определённых на отрезке [A, B]. Операции сложения векторов и умножения вектора на число – это просто сложение функций и умножение функции на число.

Определение 2. Линейной комбинацией векторов 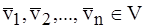наз. сумма 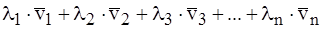, где λ ₁, λ ₂, …, λ _n 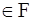- некоторые числа.

Мы говорим, что вектор 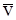можно выразить через векторы 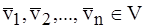, если найдутся такие λ ₁, λ ₂, …, λ _n 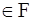, что 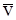можно представить в виде линейной комбинации векторов 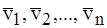, т.е. = .

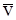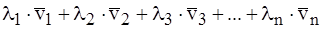Определение 3 Векторы 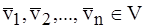наз. линейно независимыми, если ни один из них нельзя выразить через остальные.

Это определение эквивалентно следующему:

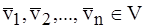линейно независимы, если из равенства 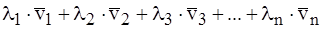= 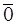следует, что все коэффициенты λ ₁, λ ₂, …, λ _n равны нулю. Действительно, если бы некоторый коэффициент, например, λ ₁ ≠ 0, то 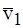выражается через остальные векторы по формуле

.

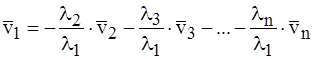Пример. Пусть рассматривается пространство функций на отрезке [-1, 1]. Тогда можно проверить, что

а) функции х и х² – линейно независимы.

б) функции 3х + 1, 2х – 1 и 7х + 2 – линейно зависимы (7х + 2 = 2.2∙ (3х + 1) + 0.2∙ (2х – 1)).

Пусть S = { 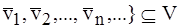- некоторое множество, конечное или бесконечное, векторов. Назовём это множество «системой векторов».

Определение 4 Рангом r системы векторов S наз. максимальное число линейно независимых векторов 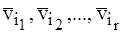, которые можно отобрать из S. (Если можно отобрать как угодно много линейно независимых векторов из S, то говорят, что S имеет бесконечный ранг).

Из определения следует, что все оставшиеся векторы выражаются через отобранные. Понятно также, что отбор неоднозначен.

Определение 5. Рангом матрицы размера (m x n) наз. ранг системы строк, рассматриваемых как векторы в пространстве Rⁿ.

Согласно определению, следовало бы говорить о строчном ранге матрицы и аналогично определить столбцовый ранг. Но оказалось, что они равны, поэтому говорят просто «ранг матрицы». Таким образом, имеет место

Теорема (о ранге матрицы). Без док-ва.

Для всякой матрицы столбцовый и строчный ранги совпадают.

Доказано также следующее

Предложение. Ранг матрицы равен порядку наибольших отличных от нуля миноров этой матрицы.

Теорема Кронекера-Капелли. Система линейных уравнений АХ = В совместна тогда и только тогда, когда ранг матрицы А равен рангу расширенной матрицы системы.

Подробного доказательства приводить не будем. Док-во основано на том, что если имеется решение Х₀, то равенство

АХ₀ = В означает, что столбец свободных членов В будет линейной комбинацией столбцов матрицы А.

Определение 6. Ранг системы всех векторов пространстваV называется его размерностью. Максимальная линейно независимая система векторов пространства V наз. его базисом.

Из определения следует, что если множество E = { 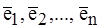} – базис V, то любой вектор 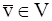можно записать в виде:

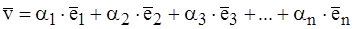. Покажем, что такое представление единственно. Действительно, пусть имеется ещё одно такое представление: 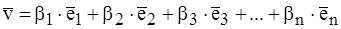. Тогда вычтем из первого равенства второе:

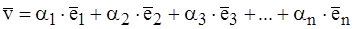
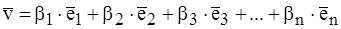
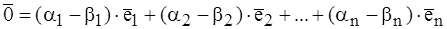
Тогда из последнего равенства следует, что все коэффициенты (α _i – β _i) = 0, т.е. α _i = β _i, так как базисные векторы линейно неза-висимы.

Определение 7. Если E = { 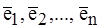} – базис V,

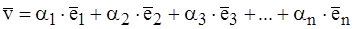, то числа α ₁, α ₂, …, α _n наз. координатами вектора 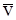в базисе Е.

Одно и то же пространство может иметь различные базисы. Только число элементов базиса (размерность пространства) неизменно.

Пример. Рассмотрим пространство R².

В качестве базисных векторов можно взять векторы 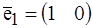и 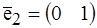. (Такой базис обычно называют «стандартным»). Тогда, например, вектор (3 -2) имеет координаты 3 и –2 в этом базисе. Если взять другие базисные векторы, например, 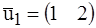и , то тот же вектор (3 -2) в новом базисе имеет координаты 1.4 и –1.6 (можно проверить: (3 -2) = 1.4∙ (1 2) – 1.6∙ (-1 3)).