
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача В13. Задания на проценты, сплавы, растворы, на движение по окружности и нахождение средней скорости
|
|
В 2010 году задание В13 пополнилось новыми задачами, и на пробном ЕГЭ для многих из вас они оказались неожиданными. Теперь задание В13 включает в себя практически все типы текстовых задач, которые раньше предлагались на вступительных экзаменах в вузы. Кроме привычных уже задач на движение и работу, появились задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.
Начнем с задач на проценты. С этой темой мы уже познакомились в задаче В1. В частности, сформулировали важное правило: за 100  мы принимаем ту величину, с которой сравниваем.
мы принимаем ту величину, с которой сравниваем.
Мы также вывели полезные формулы:
если величину  увеличить на
увеличить на 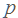 процентов, получим
процентов, получим 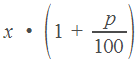 .
.
если величину  уменьшить на
уменьшить на 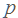 процентов, получим
процентов, получим 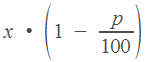 .
.
если величину  увеличить на
увеличить на 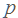 процентов, а затем уменьшить на
процентов, а затем уменьшить на 
 , получим
, получим 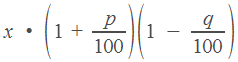 .
.
если величину  дважды увеличить на
дважды увеличить на 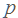 процентов, получим
процентов, получим 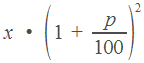
если величину  дважды уменьшить на
дважды уменьшить на 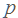 процентов, получим
процентов, получим 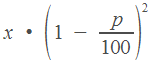
Воспользуемся ими для решения задач В13.
1. В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8  , а в 2010 году — на 9
, а в 2010 году — на 9  по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
По условию, в 2009 году число жителей выросло на 8  , то есть стало равно 40000
, то есть стало равно 40000  1, 08
1, 08  43200 человек.
43200 человек.
А в 2010 году число жителей выросло на 9  , теперь уже по сравнению с 2009 годом. Получаем, что в 2010 году в квартале стало проживать 40000
, теперь уже по сравнению с 2009 годом. Получаем, что в 2010 году в квартале стало проживать 40000  1, 08
1, 08  1, 09
1, 09  47088 жителей.
47088 жителей.
Следующая задача предлагалась на пробном ЕГЭ по математике в декабре 2010 года. Она проста, но справились с ней немногие.
2. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4  дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили  рублей. К вечеру понедельника они подорожали на
рублей. К вечеру понедельника они подорожали на 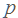
 и стали стоить
и стали стоить 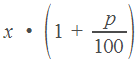 . Теперь уже эта величина принимается за 100
. Теперь уже эта величина принимается за 100  , и к вечеру вторника акции подешевели на
, и к вечеру вторника акции подешевели на 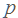
 по сравнению этой величиной. Соберем данные в таблицу:
по сравнению этой величиной. Соберем данные в таблицу:
| в понедельник утром | в понедельник вечером | во вторник вечером | |
| Стоимость акций | 
| 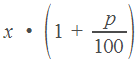
| 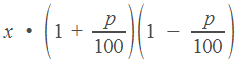
|
По условию, акции в итоге подешевели на 4  .
.
Получаем, что
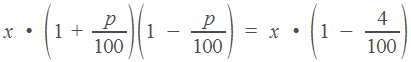
Поделим обе части уравнения на  (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения.
(ведь он не равен нулю) и применим в левой части формулу сокращенного умножения.
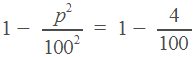
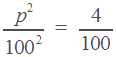
По смыслу задачи, 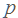 > 0.
> 0.
Получаем, что 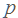
 20.
20.
3. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.
Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил 20000 рублей. Его цена два раза уменьшилась на 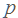
 , и теперь она равна
, и теперь она равна
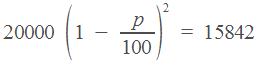
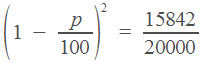
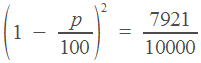
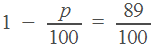
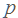
 11.
11.
4. Четыре рубашки дешевле куртки на 8  . На сколько процентов пять рубашек дороже куртки?
. На сколько процентов пять рубашек дороже куртки?
Пусть стоимость рубашки равна  , стоимость куртки
, стоимость куртки  . Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет 96
. Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет 96  от цены куртки, то есть
от цены куртки, то есть
4 
 0, 92
0, 92  .
.
Стоимость одной рубашки — в 4 раза меньше:

 0, 23
0, 23  ,
,
а стоимость пяти рубашек:
5 
 1, 15
1, 15 
 115/100
115/100 
 115
115 
 .
.
Получили, что пять рубашек на 15  дороже куртки.
дороже куртки.
Ответ: 15.
5. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67  . Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4
. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4  . Сколько процентов от общего дохода семьи составляет зарплата жены?
. Сколько процентов от общего дохода семьи составляет зарплата жены?
Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась...») назовем «ситуация А» и «ситуация В».
| муж | жена | дочь | Общий доход | |
| В реальности | 
| 
| 
|     
|
| Ситуация А | 2 
| 
| 
| 1, 67(     ) )
|
| Ситуация В | 
| 
| 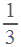 
| 0, 96(     ) )
|
Осталось записать систему уравнений.
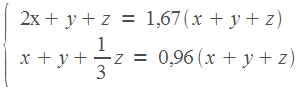
Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти  ,
,  и
и  по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму
по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму 



 . Получим:
. Получим:

 0, 67 (
0, 67 (



 )
)
Это значит, что зарплата мужа составляет 67  от общего дохода семьи.
от общего дохода семьи.
Во втором уравнении мы тоже вычтем из обеих частей выражение 



 , упростим и получим, что
, упростим и получим, что

 0, 06(
0, 06(



 )
)
Значит, стипендия дочки составляет 6  от общего дохода семьи. Тогда зарплата жены составляет 27
от общего дохода семьи. Тогда зарплата жены составляет 27  общего дохода.
общего дохода.
Ответ: 27.
Следующий тип задач — задачи на растворы, смеси и сплавы. Они встречаются не только в математике, но и в химии. Мы расскажем о самом простом способе их решения.
6. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим  .
.
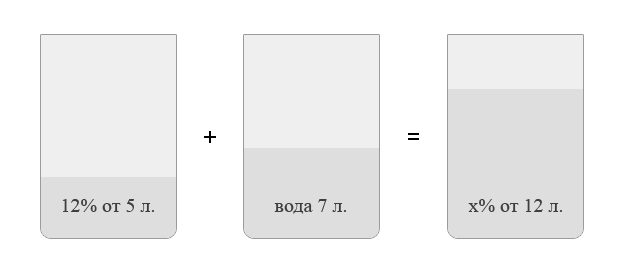
Первый сосуд содержал 0, 12  5
5  0, 6 литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
0, 6 литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
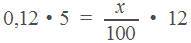

 5.
5.
7. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна  . Масса второго — тоже
. Масса второго — тоже  . В результате получили раствор массой 2
. В результате получили раствор массой 2  . Рисуем картинку.
. Рисуем картинку.
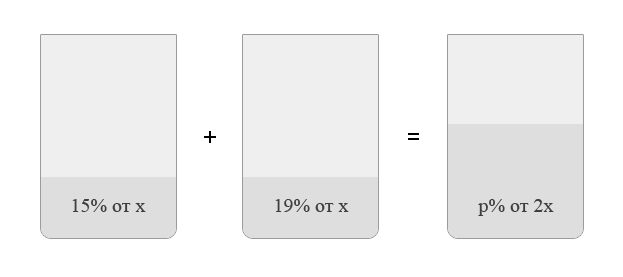
Получаем: 0, 15 
 0, 19
0, 19 
 0, 34
0, 34 
 0, 17
0, 17  2
2 
Ответ: 17.
8. Виноград содержит 90  влаги, а изюм — 5
влаги, а изюм — 5  . Сколько килограммов винограда требуется для получения 20 килограммов изюма?
. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось 90  воды, значит, «сухого вещества» было 10
воды, значит, «сухого вещества» было 10  . В изюме 5
. В изюме 5  воды и 95
воды и 95  «сухого вещества». Пусть из
«сухого вещества». Пусть из  кг винограда получилось 20 кг изюма. Тогда
кг винограда получилось 20 кг изюма. Тогда
10  от
от 
 95
95  от 20
от 20
Составим уравнение:
0, 1 
 0, 95
0, 95  20
20
и найдем  .
.
Ответ: 190.
9. Имеется два сплава. Первый сплав содержит 10  никеля, второй — 30
никеля, второй — 30  никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25
никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25  никеля. На сколько килограммов масса первого сплава меньше массы второго?
никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна  , а масса второго равна
, а масса второго равна  . В результате получили сплав массой
. В результате получили сплав массой 


 200.
200.
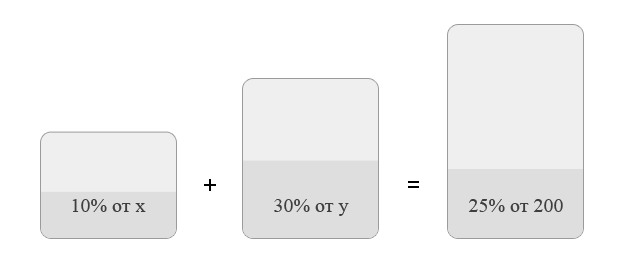
Запишем простую систему уравнений:
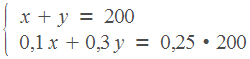
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что 
 50,
50, 
 150.
150.
Ответ: 100.
10. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Пусть масса первого раствора  , масса второго равна
, масса второго равна  . Масса получившегося раствора равна
. Масса получившегося раствора равна 


 10. Запишем два уравнения, для количества кислоты.
10. Запишем два уравнения, для количества кислоты.
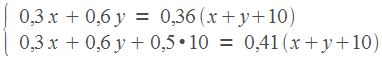
Решаем получившуюся систему. Сразу умножим обе части уравнений на 100, поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
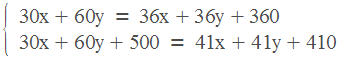
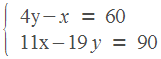

 60;
60; 
 30
30
Ответ: 60.
Задачи на движение по окружности также оказались сложными для многих школьников. Решаются они почти так же, как и обычные задачи на движение. В них тоже применяется формула 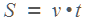 . Но есть одна хитрость, о которой мы расскажем.
. Но есть одна хитрость, о которой мы расскажем.
11. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за  и
и  . В первый раз мотоциклист обогнал велосипедиста через 10 минут, то есть через
. В первый раз мотоциклист обогнал велосипедиста через 10 минут, то есть через 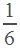 часа после старта. До этого момента велосипедист был в пути 40 минут, то есть
часа после старта. До этого момента велосипедист был в пути 40 минут, то есть 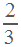 часа.
часа.
Запишем эти данные в таблицу:
| v | t | S | |
| велосипедист | 
| 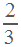
| 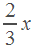
|
| мотоциклист | 
| 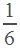
| 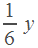
|
Оба проехали одинаковые расстояния, то есть 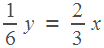 .
.
Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через 30 минут, то есть через  часа после первого обгона.
часа после первого обгона.
Нарисуем вторую таблицу.
| v | t | S | |
| велосипедист | 
| 
| 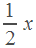
|
| мотоциклист | 
| 
| 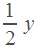
|
А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна 30 км. Получим второе уравнение:
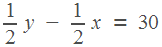
Решим получившуюся систему.
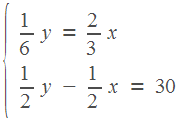
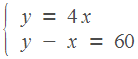
Получим, что 
 20,
20, 
 80. В ответ запишем скорость мотоциклиста.
80. В ответ запишем скорость мотоциклиста.
Ответ: 80.
12. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Это, пожалуй, самая сложная задача В13. Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через 4 часа, ровно в 12.00.
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?
За один час минутная стрелка проходит один круг, а часовая 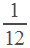 часть круга. Пусть их скорости равны 1 (круг в час) и
часть круга. Пусть их скорости равны 1 (круг в час) и 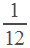 (круга в час). Старт — в 8.00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.
(круга в час). Старт — в 8.00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.
Минутная стрелка пройдет на 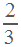 круга больше, поэтому уравнение будет таким:
круга больше, поэтому уравнение будет таким:
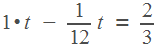
Решив его, получим, что  часа. Итак, в первый раз стрелки поравняются через
часа. Итак, в первый раз стрелки поравняются через 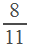 часа. Пусть во второй раз они поравняются через время
часа. Пусть во второй раз они поравняются через время  . Минутная стрелка пройдет расстояние 1
. Минутная стрелка пройдет расстояние 1 
 , а часовая
, а часовая 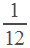

 , причем минутная стрелка пройдет на один круг больше. Запишем уравнение:
, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:
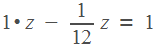
Решив его, получим, что 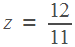 часа. Итак, через
часа. Итак, через  часа стрелки поравняются во второй раз, еще через
часа стрелки поравняются во второй раз, еще через  часа — в третий, и еще через
часа — в третий, и еще через  часа — в четвертый.
часа — в четвертый.
Значит, если старт был в 8.00, то в четвертый раз стрелки поравняются через  часа.
часа.
Ответ полностью согласуется с «экспериментальным» решением!: -)
На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:
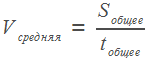 .
.
Если участков пути было два, то
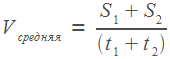
13. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем только, что это расстояние было одинаковым на пути туда и обратно. Для простоты примем это расстояние за 1 (одно море). Тогда время, которое путешественник плыл на яхте, равно 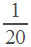 , а время, затраченное на полет, равно
, а время, затраченное на полет, равно 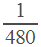 . Общее время равно
. Общее время равно 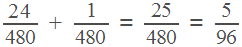 .
.
Средняя скорость равна 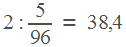 км/ч.
км/ч.
Ответ: 38, 4.
Покажем еще один эффектный прием, помогающий быстро решить систему уравнений в задаче В13.
14. Андрей и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Андрей — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Мы уже решали задачи на работу и производительность. Правила те же. Отличие лишь в том, что здесь работают трое, и переменных будет тоже три. Пусть  — производительность Андрея,
— производительность Андрея,  — производительность Паши, а
— производительность Паши, а  — производительность Володи. Забор, то есть величину работы, примем за 1 — ведь мы ничего не можем сказать о его размере.
— производительность Володи. Забор, то есть величину работы, примем за 1 — ведь мы ничего не можем сказать о его размере.
| производительность | работа | |
| Андрей | 
| |
| Паша | 
| |
| Володя | 
| |
| Вместе |     
|
Андрей и Паша покрасили забор за 9 часов. Мы помним, что при совместной работе производительности складываются. Запишем уравнение:
(

 )
)  9
9  1
1
Аналогично,
(

 )
)  12
12  1
1
(

 )
)  12
12  1.
1.
Тогда




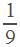




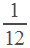




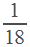 .
.
Можно искать  ,
,  и
и  по отдельности, но лучше просто сложить все три уравнения. Получим, что
по отдельности, но лучше просто сложить все три уравнения. Получим, что
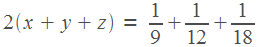 .
.
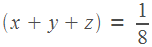 .
.
Значит, работая втроем, Андрей, Паша и Володя красят за час одну восьмую часть забора. Весь забор они покрасят за 8 часов.
Ответ: 8.
В следующей статье мы расскажем о том, что такое арифметическая прогрессия, и на этом завершим обзор задач В13.
Весь банк заданий ФИПИ по математике вы можете найти на официальном сайте mathege.ru.