Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общие сведения о фазоповоротных схемах
|
|
При реализации реле защиты различных типов (реле направления мощности, реле сопротивления, реле симметричных составляющих), возникает необходимость изменения фаз синусоидальных токов или напряжений. Обычно это достигается применением специальных фазоповоротных схем (ФПС). Их действие основано на влиянии соотношения активных и реактивных составляющих полного сопротивления цепи на угол сдвига фаз между входными и выходными токами и (или) напряжениями. Различают управляемые и неуправляемые ФПС.
Неуправляемые ФПС обеспечивают некоторый постоянный угол сдвига фаз 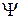 между входной и выходной электрическими величинами.
между входной и выходной электрическими величинами.
Угол сдвига фаз управляемых ФПС может изменяться по заданному закону (по воле оператора). Примером управляемой ФПС является фазовращатель (рисунок 2.11). Фаза его выходного напряжения зависит от взаимного расположения подвижной части (ротора) относительно неподвижной (статора). При плавном повороте ротора фазовращателя в пределах от
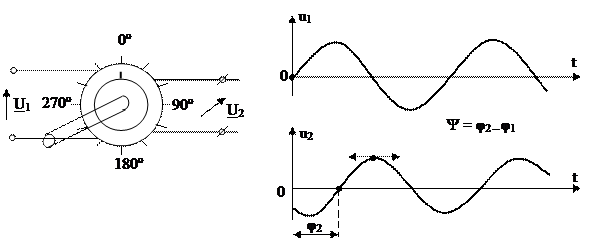
Рисунок 2.11 Условное обозначение фазовращателя
0º до 360º также плавно в пределах от нуля до 360º электрических градусов изменяется фаза 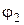 выходного напряжения
выходного напряжения 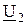 . При обратном повороте штурвала фазовращателя угол
. При обратном повороте штурвала фазовращателя угол 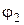 уменьшается. Таким образом, с помощью фазовращателя можно обеспечить угол сдвига фаз
уменьшается. Таким образом, с помощью фазовращателя можно обеспечить угол сдвига фаз 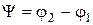 между входным напряжением
между входным напряжением 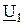 и выходным -
и выходным - 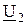 в пределах от 0º до 360º.
в пределах от 0º до 360º.
Фазовращатели находят широкое применение при лабораторных (стендовых) испытаниях различных реле защиты.
Проходная характеристика ФПС в общем виде может быть представлена выражением
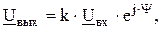 где (2.8)
где (2.8)
k – коэффициент пропорциональности, учитывающий потери в ФПС.
Наиболее распространенными неуправляемыми ФПС являются мостовые ФПС с конденсаторами и катушками индуктивности.
2.4 RC – фазоповоротные схемы
На рисунке 2.12 приведена мостовая RC-фазоповоротная схема. Для простоты рассуждений примем R1=R2 и C1=C2.
К участкам цепи R1, C1 и R2, C2 приложено входное напряжение 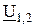 . Токи
. Токи 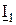 и
и 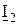 из-за активно-емкостного характера сопротивления участков цепи опережают приложенное к ним напряжение
из-за активно-емкостного характера сопротивления участков цепи опережают приложенное к ним напряжение 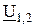 на угол
на угол 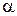 . Величина угла
. Величина угла 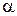 определяется соотношением сопротивлений
определяется соотношением сопротивлений 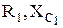 и
и 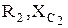 . При равенстве сопротивлений R1=R2, а также
. При равенстве сопротивлений R1=R2, а также 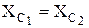 эти токи равны по величине и совпадают по фазе, т.е.
эти токи равны по величине и совпадают по фазе, т.е. 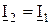 .
.
Ток 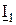 протекая по резистору R1, создает на нем падение напряжения
протекая по резистору R1, создает на нем падение напряжения 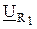 , совпадающее по фазе с током
, совпадающее по фазе с током 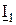 .
.
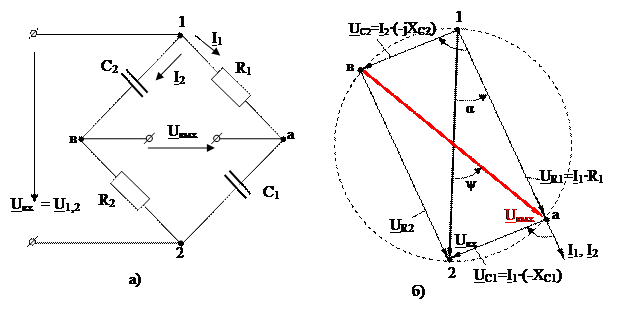
Рисунок 2.12 Мостовая RC – фазоповоротная схема а); векторно-топографическая диаграмма RC – ФПС.б)
Напряжение на конденсаторе C1 отстает от тока 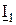 на 90º. Вектор входного напряжения
на 90º. Вектор входного напряжения 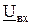 равен геометрической сумме векторов напряжений
равен геометрической сумме векторов напряжений 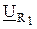 и
и 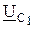 , т.е.
, т.е.
 (2.9)
(2.9)
Аналогично для левой ветви
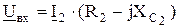 (2.10)
(2.10)
Вектор  на векторно- топографической диаграмме (точки в, а) представляет собой напряжение на выходе ФПС, работающей в режиме холостого хода (х.х.).
на векторно- топографической диаграмме (точки в, а) представляет собой напряжение на выходе ФПС, работающей в режиме холостого хода (х.х.).
Угол 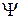 - угол сдвига фаз между напряжениями
- угол сдвига фаз между напряжениями 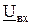 и
и  .
.
Из векторно-топографической диаграммы следует, что
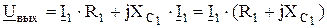 (2.11)
(2.11)
Поделим левую и правую части выражения 2.9 на левую и правую части выражения 2.11. Получим
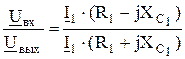 .
.
Отсюда выходное напряжение холостого хода
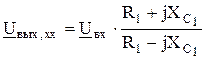 (2.12)
(2.12)
Угол сдвига фаз 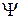 между
между 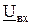 и
и 
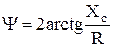 (2.13)
(2.13)
Действительно, в треугольнике 1, 2, а (рисунок 2.12, б) угол 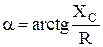 , а угол
, а угол 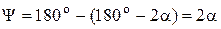 .
.
Анализ выражений (2.12) и (2.13) позволяет сделать следующий вывод.
В случае равенства всех сопротивлений, то есть, при 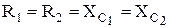 угол
угол 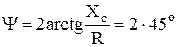 (рисунок 2.13, б).
(рисунок 2.13, б).
При уменьшении емкостных сопротивлений 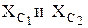 (при увеличении емкостей) точки а и в, перемещаясь по дугам окружности, стремятся к точкам 2 и 1 соответственно (рисунок 2.13, а), при этом угол
(при увеличении емкостей) точки а и в, перемещаясь по дугам окружности, стремятся к точкам 2 и 1 соответственно (рисунок 2.13, а), при этом угол 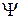 уменьшается. В пределе, когда
уменьшается. В пределе, когда 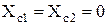 , точка а совпадает с точкой 2, а точка в совпадает с точкой 1. В этом случае ФПС имеет лишь активную составляющую полного сопротивления, а угол
, точка а совпадает с точкой 2, а точка в совпадает с точкой 1. В этом случае ФПС имеет лишь активную составляющую полного сопротивления, а угол 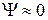 . При увеличении
. При увеличении  и уменьшении R угол
и уменьшении R угол 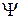 возрастает, в пределе стремясь к
возрастает, в пределе стремясь к 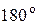 .
.
Таким образом, подбирая величины сопротивлений 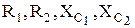 , можно получить угол сдвига фаз между входным напряжением и выходным в пределах от 0º до 180º.
, можно получить угол сдвига фаз между входным напряжением и выходным в пределах от 0º до 180º.
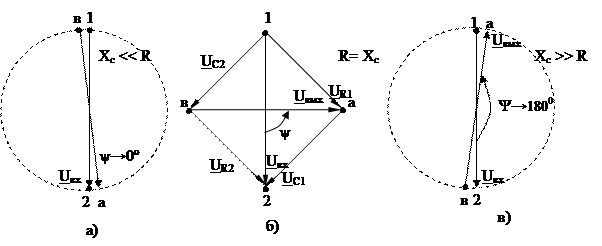
Рисунок 2.13 Зависимость угла сдвига фаз ψ ФПС от соотношения R и Хс
Достоинством рассмотренной схемы является ее простота. Недостатком схемы является то, что при несимметрии плеч (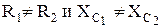 ) искажается амплитуда выходного напряжения. Это наглядно иллюстрируется рисунком 2.14. При симметрии плеч выходное напряжение
) искажается амплитуда выходного напряжения. Это наглядно иллюстрируется рисунком 2.14. При симметрии плеч выходное напряжение 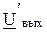 максимально (на рисунке показано пунктирной линией).
максимально (на рисунке показано пунктирной линией).
 |
Рисунок 2.14
При 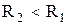 и
и 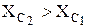 выходное напряжение
выходное напряжение  становится меньше
становится меньше 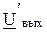 . Кроме того, искажается и угол
. Кроме того, искажается и угол 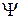 .
.
При подключении к выходным зажимам ФПС (точки в и а) нагрузки 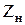 векторно-топографическая диаграмма видоизменяется. Напряжение на выходе ФПС уменьшается
векторно-топографическая диаграмма видоизменяется. Напряжение на выходе ФПС уменьшается
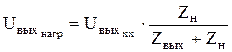 , (2.14)
, (2.14)
где 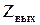 - выходное сопротивление ФПС.
- выходное сопротивление ФПС.
В общем случае в нагрузочном режиме изменяется и угол 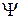 . Все это в каждом конкретном случае требует доработки схемы.
. Все это в каждом конкретном случае требует доработки схемы.
2.5 RL – фазоповоротные схемы
На рисунке 2.15 приведена активно-индуктивная фазоповоротная схема. Промежуточный трансформатор TL имеет вторичную обмотку, состоящую из двух одинаковых секций. Секции включены согласно.
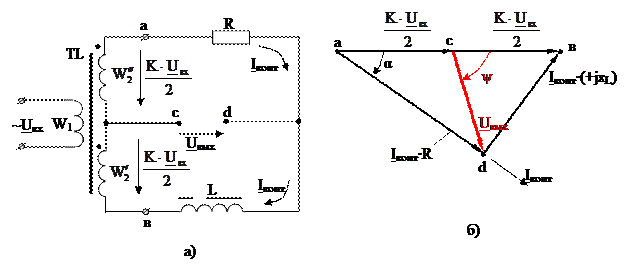
Рисунок 2.15 Схема RL фазоповоротной схемы и её векторно-топографическая диаграмма
В точках а и в элементы ФПС подключены ко вторичной обмотке на суммарное напряжение 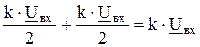 . Под действием напряжения
. Под действием напряжения 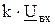 в контуре фазоповоротной схемы проходит ток
в контуре фазоповоротной схемы проходит ток 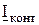 , который отстает от приложенного напряжения
, который отстает от приложенного напряжения 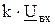 на некоторый угол
на некоторый угол 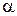 . Величина угла
. Величина угла 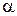 зависит от соотношения активных и реактивных составляющих полного сопротивления контура.
зависит от соотношения активных и реактивных составляющих полного сопротивления контура.
Ток контура 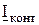 , проходя по резистору R, создает на нем падение напряжения
, проходя по резистору R, создает на нем падение напряжения 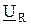 , равное
, равное 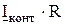 и совпадающее по фазе с током.
и совпадающее по фазе с током.
Напряжение на дросселе, равное  опережает ток в контуре на 90º. Сумма напряжений на резисторе и на дросселе равна напряжению, приложенному в точках а и в к элементам ФПС, т.е.
опережает ток в контуре на 90º. Сумма напряжений на резисторе и на дросселе равна напряжению, приложенному в точках а и в к элементам ФПС, т.е.
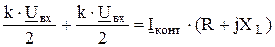 (2.15)
(2.15)
В режиме х.х. напряжение на выходе ФПС (точки c и d на векторно-топографической диаграмме)
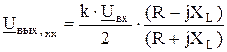 (2.16)
(2.16)
Примечание. Из векторно-топографической диаграммы следует:
1) 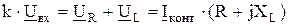 ; (2.17)
; (2.17)
2) 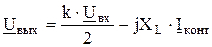 (2.18)
(2.18)
В выражении 2.18 заменим 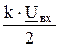 его значением, которое следует из диаграммы
его значением, которое следует из диаграммы
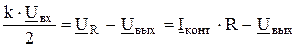 (2.19)
(2.19)
Учитывая 2.18 и 2.19, можно записать
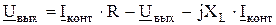 (2.20)
(2.20)
Или  (2.21)
(2.21)
Теперь разделим левую и правую части выражения (2.21) на соответствующие части выражения 2.17
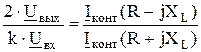 ; отсюда
; отсюда
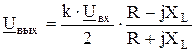 , т.е. мы пришли к выражению (2.16).
, т.е. мы пришли к выражению (2.16).
Угол сдвига фаз между входным напряжением и выходным
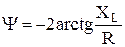 (2.22)
(2.22)
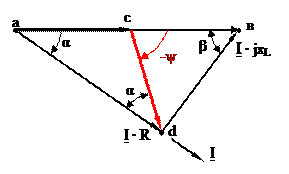 Примечание. Покажем правильность выражения (2.22). На векторно-топографической диаграмме обозначим угол при вершине в треугольника
Примечание. Покажем правильность выражения (2.22). На векторно-топографической диаграмме обозначим угол при вершине в треугольника 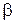 (рисунок 2.16).
(рисунок 2.16).
Тогда из треугольника 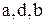
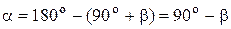
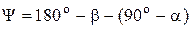
Рисунок 2.16
В последнем выражении вместо 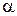 подставим его значение
подставим его значение
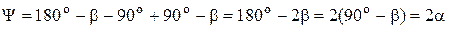
Знак «-» в выражении 2.22 указывает на то, что выходное напряжение  отстает по фазе от входного
отстает по фазе от входного 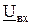 .
.
|
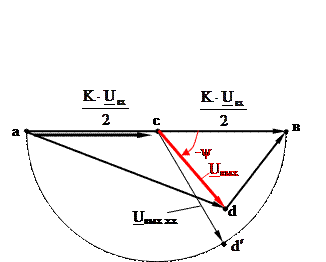 |
Рисунок 2.16 Векторно-топографическая диаграмма RL – фазоповоротной схемы в нагрузочном режиме
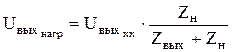 , где
, где