
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Finally
|
|
Close(fDat); Close(fRes);
end;
end.
 Тема 3. Бинарные деревья
Тема 3. Бинарные деревья
1. Основные понятия и определения
Дерево – это непустое конечное множество элементов, из которых один называется корнем, а остальные делятся на несколько непересекающихся подмножеств, каждое из которых само является деревом.
Рекурсивное определение. Дерево с базовым типом Т – это либо: пустое дерево, либо некоторый узел типа Т с некоторым конечным числом связанных с ним деревьев типа Т, называемых поддеревьями.
Существует несколько способов изображения структуры дерева: вложенные множества (1), вложенные скобки (2), отступы (3), граф (4). Ниже с помощью перечисленных способов изображено одно и то же дерево, элементами которого являются буквы латинского алфавита:
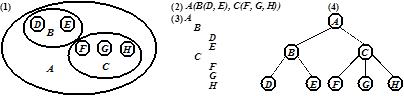
Структура, представленная в виде графа и явно отражающая разветвления, привела к появлению термина «дерево». Каждый элемент дерева называют узлом. Дерево принято изображать растущим вниз, а его верхний узел называют корнем. Все узлы дерева разбивают на уровни. Корень имеет нулевой уровень. Если узел x лежит на уровне i, а y связана с x и лежит на уровне i +1, то говорят, что y – потомок (сын) x, а x – предок (отец) y. Высота дерева равна максимальному уровню этого дерева плюс 1.
Если элемент не имеет потомков, то его называют терминальным узлом, или листом, в противном случае узел называют внутренним. Число непосредственных потомков внутреннего узла называют его степенью. Максимальная степень всех узлов есть степень дерева.
Упорядоченное дерево – это дерево, у которого ветви, исходящие из каждого узла, упорядочены. Поэтому два изображенных ниже упорядоченных дерева – это разные объекты.
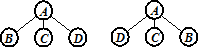
Особенно важную роль играют упорядоченные деревья второй степени. Их называют двоичными (или бинарными) деревьями.
Примеры бинарного дерева: генеалогическое дерево, где у каждого человека есть потомки (!) в лице отца и матери; схема кубкового спортивного турнира, где каждая игра – это узел, в котором указан её победитель, а потомки – две предыдущие игры соперников; арифметическое выражение с бинарными операциями, где каждому оператору соответствует узел, а операнды – его поддеревья. Ниже приведены два бинарных дерева: дерево (а), элементами которого являются символы латинского алфавита, и дерево (б) выражения (a + b / c)´ (d – e ´ f).
(а) (б)
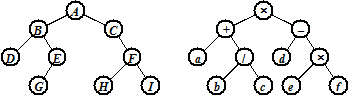
Если каждый узел бинарного дерева, не являющийся листом, имеет непустые правые и левые поддеревья, то дерево называется строго бинарным. Строго бинарное дерево с n листами всегда содержит 2 n -1 узлов. Дерево выражения (б) является строго бинарным.
Строго бинарное дерево, все листья которого расположены на одном уровне, называется совершенным. Совершенное дерево высотой h содержит 2 h –1 узлов. На каждом его уровне расположено максимальное количество узлов, равное 2 i, где i – номер уровня.
2. Построение бинарного дерева
Наибольший интерес представляет задача построения дерева минимальной высоты при заданном числе узлов n. Очевидно, что минимальная высота достигается, если на всех уровнях, кроме последнего, помещается максимально возможное число узлов. Этого можно добиться, размещая очередные узлы поровну слева и справа от каждого узла. В результате будем получать деревья со следующей структурой:
n =1 n =2 n =3 n =4 n =5 n =6 n =7
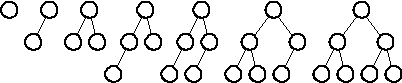
Правило равномерного распределения для известного числа узлов n лучше всего сформулировать, используя рекурсию:
1) взять один узел в качестве корня;
2) построить тем же способом левое поддерево с nl = n div 2 узлами;
3) построить тем же способом правое поддерево с nr = n – nl –1 узлом.
Построенное с помощью предложенного выше алгоритма дерево будет идеально сбалансированным – для каждого его узла число узлов в правых и левых поддеревьях отличается не более чем на 1.
3. Операции над бинарным деревом
Над бинарным деревом могут быть выполнены операции:
Ø обход узлов бинарного дерева в определенном порядке;
Ø добавление некоторого поддерева в дерево;
Ø исключение некоторого поддерева из дерева;
Ø примитивные операции над узлами дерева.
Обход (прохождение) дерева используется для систематического последовательного просмотра узлов дерева. Эта операция может быть использована для контроля информации, хранящейся в древовидной структуре, а также как составная часть для выполнения других операций над деревом. Рекурсивная процедура обхода дерева включает в себя следующие шаги:
1) обработка (просмотр) корня дерева или поддерева;
2) обход левого поддерева обработанного корня;
3) обход правого поддерева обработанного корня;
Различный порядок выполнения перечисленных выше шагов определяет три процедуры обхода бинарного дерева:
1) обход сверху вниз – сначала обрабатывается корень, затем обходится его левое, затем правое поддеревья (операция UpDownRevision);
2) обход слева направо – сначала обходится левое поддерево корня, затем обрабатывается корень, затем обходится его правое поддерево (операция LeftRightRevision);
3) обход снизу вверх – обходится левое поддерево корня, затем правое, затем обрабатывается корень (операция DownUpRevision).
При обходе каждого из приведённых ниже бинарных деревьев получим по три упорядоченные последовательности:
(а) (б)

обходдерево (а)дерево (б)
сверху вниз ABDEGCFHI ´ + a / bc – d ´ ef (префиксная запись)
слева направо DBGEACHFI a + b / c ´ d – e ´ f (инфиксная без скобок)
снизу вверх DGEBHIFCA abc /+ def ´ –´ (постфиксная запись)
Добавление некоторого поддерева в дерево. Для выполнения этой операции должны быть заданы: включаемое поддерево и узел исходного дерева, к которому поддерево подключается в качестве ветви. Поскольку бинарное дерево является упорядоченным, то должно быть указание на то, в качестве какой ветви (левой или правой) заданного узла должно быть подключено поддерево. Целесообразно разбить эту операцию на две: включение поддерева в качестве левой ветви заданного узла (AddLeft) и включение в качестве правой ветви заданного узла (AddRight). Ветви, в которые осуществляется включение, должны быть пустыми.
Исключение некоторого поддерева из дерева фактически представляет собой две операции: исключение поддерева из левой ветви заданного узла исходного дерева (DeleteLeft) и исключение поддерева из его правой ветви (DeleteRight). Операция возвращает адрес исключенного поддерева.
Примитивные операции над узлами бинарного дерева могут быть следующими. Addr(v) возвращает адрес узла со значением v. Если p – указатель на узел Node бинарного дерева, то операция Value(p) возвращает значение узла Node. Операции Left(p), Right(p), Father(p), Brother(p) возвращают соответственно указатели на левого сына, правого сына, отца и брата узла Node. Операции IsLeft(p) и IsRight(p) возвращают значение «истина», если Node является соответственно левым или правым сыном некоторого узла дерева, и значение «ложь» – в противном случае.
Дополнительно могут быть определены следующие операции: Create – создание пустого дерева, Clear – удаление всех узлов дерева, WriteTo (f) – вывод дерева в файл f с помощью отступов, NodesQuantity – определение числа узлов дерева.
4. Реализация бинарного дерева
При реализации дерева с помощью динамических переменных каждый элемент дерева, помимо информационной части, содержит два указателя: на левое и правое поддеревья этого элемента. Переменная ссылочного типа fRoot указывает на корневой узел дерева. Если какой-либо узел дерева не имеет левого или правого поддерева, то соответствующий указатель этого узла содержит значение nil.
Описание класса tBinaryTree:
Type
tValue = Char; // тип элемента дерева - символьный
pItem = ^tItem; // тип указателя на элемент дерева
tItem = record // элемент дерева
Value: tValue; // содержательная часть элемента дерева
Left, Right: pItem; // указатели на левое и правое поддеревья
end; // tItem
tBinaryTree= class // класс - бинарное дерево