Else Begin

r: =a Mod b;

RecEuclid(b, r, d);

End;

End;

Этот алгоритм, в принципе, выполняет те же вычисления, что и итеративный. Определяется цепочка остатков до наибольшего общего делителя. 2322, 654, 360, 294, 66, 30, 6, 0, при этом вся цепочка запоминается. Кроме того, в соответствии с логикой работы рекурсивных схем реализации осуществляется возврат к началу вычислений (выход из рекурсии). В данном случае «налегке», «в холостую». Вот здесь-то, на обратном пути, мы и «заставим» его работать.

Завершив прямой проход, процедура «смотрит» на два последних числа в цепочке. На b и r. Наибольший общий делитель d равен b. Выразим его через b и r: d=b· 1 +r· 0.

Внимание – снова вопрос. Есть a= q ∙ b+r, 0≤ r< b и известно представление d с помощью b и r: d=b· x^/ +r· y^/. Как найти представление d с помощью aи b?

Ответ. Так как r=a-q∙ b, то d=b· x^/ +r· y^/ =b· x^/ +(a-q∙ b)· y^/ =a· y^/ +b· (x^/- q ∙ y^/),

или d=a· x +b· y, где

x = y^/, y = x^/ -q∙ y^/.

Итак, нам известно, с чего начать обратный путь и как делать шаг по цепочке назад. По формулам выражаем d уже через пару предпоследних чисел в цепочке, продолжаем выходить из рекурсии до тех пор, пока не выразим d через первые два числа.

Пример. Пустьa=2322 и b=654. Строим таблицу (рис. 1.22) в два этапа. На первом – сверху вниз – находим частные и остатки от делений. На втором – снизу вверх – вычисляем множители x и y.

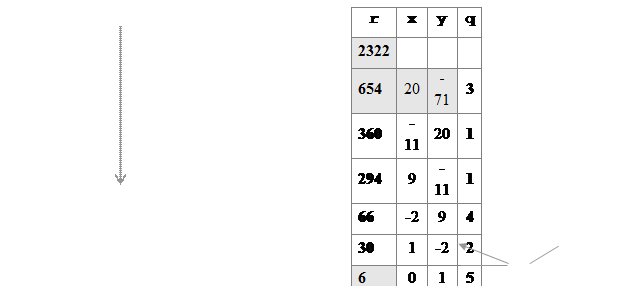
Рис. 1.22. Пример вычисления представления d в виде a·x+b·y с помощью рекурсивной логики

В самую нижнюю строку автоматически заносим 1 и 0. Это очевидное представление наибольшего общего делителя d= 6, с помощью 6 и 0: 6 =6· 1 +0· 0.

Заполняем вторую строку снизу. Значение x= 0 просто переносим «по диагонали» из строки ниже. Вычисляем y=1-0·5= 1. Это представление d с помощью 30 и 6: 6 =30· 0 +6· 1.

Определяем третью строку. Значение x= 1 в новь берём «по диагонали» из строки ниже, а значение y=0-1·2= -2. Это представление d с помощью 66 и 30. 6 =66· 1 +30· ( - 2).

«Всё выше и выше». В результате, выразим d через 2322 и 654. Как и в итеративной версии, НОД(2322, 654)= 6 =2322· 20 +654·(- 71).

Программная реализация имеет вид.

Procedure RecExEuclid (a, b: Integer; Var d, x, y: Integer);

Var r, q, x1, y1: Integer;

Begin

If b=0 Then Begin

d: =a;

x: =1; y: =0;

End