
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение регрессии.
|
|
Уравнение регрессии выглядит следующим образом: Y=a+b*X
При помощи этого уравнения переменная Y выражается через константу a и угол наклона прямой (или угловой коэффициент) b, умноженный на значение переменной X. Константу a также называют свободным членом, а угловой коэффициент - коэффициентом регрессии или B-коэффициентом.
В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой.
Остаток - это отклонение отдельной точки (наблюдения) от линии регрессии (предсказанного значения).
Для решения задачи регрессионного анализа в MS Excel выбираем в меню Сервис " Пакет анализа" и инструмент анализа " Регрессия". Задаем входные интервалы X и Y. Входной интервал Y - это диапазон зависимых анализируемых данных, он должен включать один столбец. Входной интервал X - это диапазон независимых данных, которые необходимо проанализировать. Число входных диапазонов должно быть не больше 16.
На выходе процедуры в выходном диапазоне получаем отчет, приведенный в таблице 8.3а - 8.3в.
ВЫВОД ИТОГОВ
| Таблица 8.3а. Регрессионная статистика | |
| Регрессионная статистика | |
| Множественный R | 0, 998364 |
| R-квадрат | 0, 99673 |
| Нормированный R-квадрат | 0, 996321 |
| Стандартная ошибка | 0, 42405 |
| Наблюдения |
Сначала рассмотрим верхнюю часть расчетов, представленную в таблице 8.3а, - регрессионную статистику.
Величина R-квадрат, называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью (расчетными данными). Мера определенности всегда находится в пределах интервала [0; 1].
В большинстве случаев значение R-квадрат находится между этими значениями, называемыми экстремальными, т.е. между нулем и единицей.
Если значение R-квадрата близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R-квадрата, близкое к нулю, означает плохое качество построенной модели.
В нашем примере мера определенности равна 0, 99673, что говорит об очень хорошей подгонке регрессионной прямой к исходным данным.
множественный R - коэффициент множественной корреляции R - выражает степень зависимости независимых переменных (X) и зависимой переменной (Y).
Множественный R равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы.
В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона. Действительно, множественный R в нашем случае равен коэффициенту корреляции Пирсона из предыдущего примера (0, 998364).
| Таблица 8.3б. Коэффициенты регрессии | |||
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | 2, 694545455 | 0, 33176878 | 8, 121757129 |
| Переменная X 1 | 2, 305454545 | 0, 04668634 | 49, 38177965 |
| * Приведен усеченный вариант расчетов |
Теперь рассмотрим среднюю часть расчетов, представленную в таблице 8.3б. Здесь даны коэффициент регрессии b (2, 305454545) и смещение по оси ординат, т.е. константа a (2, 694545455).
Исходя из расчетов, можем записать уравнение регрессии таким образом:
Y= x*2, 305454545+2, 694545455Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициентов регрессии (коэффициента b).
Если знак при коэффициенте регрессии - положительный, связь зависимой переменной с независимой будет положительной. В нашем случае знак коэффициента регрессии положительный, следовательно, связь также является положительной.
Если знак при коэффициенте регрессии - отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).
В таблице 8.3в. представлены результаты вывода остатков. Для того чтобы эти результаты появились в отчете, необходимо при запуске инструмента " Регрессия" активировать чекбокс " Остатки".
ВЫВОД ОСТАТКА
| Таблица 8.3в. Остатки | |||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 9, 610909091 | -0, 610909091 | -1, 528044662 | |
| 7, 305454545 | -0, 305454545 | -0, 764022331 | |
| 11, 91636364 | 0, 083636364 | 0, 209196591 | |
| 14, 22181818 | 0, 778181818 | 1, 946437843 | |
| 16, 52727273 | 0, 472727273 | 1, 182415512 | |
| 18, 83272727 | 0, 167272727 | 0, 418393181 | |
| 21, 13818182 | -0, 138181818 | -0, 34562915 | |
| 23, 44363636 | -0, 043636364 | -0, 109146047 | |
| 25, 74909091 | -0, 149090909 | -0, 372915662 | |
| 28, 05454545 | -0, 254545455 | -0, 636685276 |
При помощи этой части отчета мы можем видеть отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение остатка в нашем случае - 0, 778, наименьшее - 0, 043. Для лучшей интерпретации этих данных воспользуемся графиком исходных данных и построенной линией регрессии, представленными на рис. 8.3. Как видим, линия регрессии достаточно точно " подогнана" под значения исходных данных.
Следует учитывать, что рассматриваемый пример является достаточно простым и далеко не всегда возможно качественное построение регрессионной прямой линейного вида.
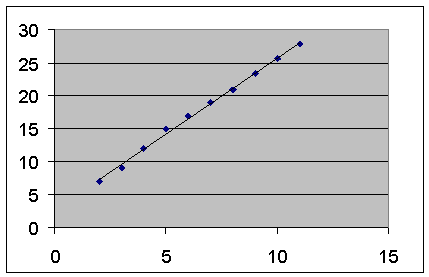
Рис. 8.3. Исходные данные и линия регрессии
Осталась нерассмотренной задача оценки неизвестных будущих значений зависимой переменной на основании известных значений независимой переменной, т.е. задача прогнозирования.
Имея уравнение регрессии, задача прогнозирования сводится к решению уравнения Y= x*2, 305454545+2, 694545455 с известными значениями x. Результаты прогнозирования зависимой переменной Y на шесть шагов вперед представлены в таблице 8.4.
| Таблица 8.4. Результаты прогнозирования переменной Y | |
| x | Y(прогнозируемое) |
| 28, 05455 | |
| 30, 36 | |
| 32, 66545 | |
| 34, 97091 | |
| 37, 27636 | |
| 39, 58182 |
Таким образом, в результате использования регрессионного анализа в пакете Microsoft Excel мы:
- построили уравнение регрессии;
- установили форму зависимости и направление связи между переменными - положительная линейная регрессия, которая выражается в равномерном росте функции;
- установили направление связи между переменными;
- оценили качество полученной регрессионной прямой;
- смогли увидеть отклонения расчетных данных от данных исходного набора;
- предсказали будущие значения зависимой переменной.
Если функция регрессии определена, интерпретирована и обоснована, и оценка точности регрессионного анализа соответствует требованиям, можно считать, что построенная модель и прогнозные значения обладают достаточной надежностью.
Прогнозные значения, полученные таким способом, являются средними значениями, которые можно ожидать.
Выводы
В этой части лекции мы рассмотрели основные характеристики описательной статистики и среди них такие понятия, как среднее значение, медиана, максимум, минимум и другие характеристики вариации данных. Также было кратко рассмотрено понятие выбросов. Рассмотренные в лекции характеристики относятся к так называемому исследовательскому анализу данных, его выводы могут относиться не к генеральной совокупности, а лишь к выборке данных. Исследовательский анализ данных используется для получения первичных выводов и формирования гипотез относительно генеральной совокупности. Также были рассмотрены основы корреляционного и регрессионного анализа, их задачи и возможности практического использования.