Начальные и центральные теоретические моменты

Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

Найдем начальный момент первого порядка (k=1):

т.е. начальный момент первого порядка случайной величины X – это ее математическое ожидание.

Найдем начальный момент второго порядка (k=2):

т.о. начальный момент второго порядка случайной величины X – математическое ожидание случайной величины X². Учитывая выражение (5.4) и полученные соотношения, можно выразить дисперсию случайной величины X через ее начальные моменты:

(5.7)

Центральным моментом порядка k случайной величины X называют математическое ожидание величины

Найдем центральный момент первого порядка (k=1):

по свойству 5 математического ожидания.

Найдем центральный момент второго порядка (k=2):

согласно выражению (5.3).

Сопоставление последнего соотношения и (5.7) позволяет получить связь между начальными и центральными моментами случайной величины X:

Распределения дискретных случайных величин

Биномиальное распределение. Дискретная случайная величина Х имеет биномиальное распределение, если ее возможные значения 0, 1, 2,..., m, …, n, а соответствующие им вероятности равны:

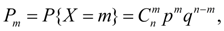(21)

где 0 < p < 1, q = 1 – p; m = 0, 1, 2,..., n.

Как видно из (21), вероятности Рm вычисляются, как члены разложения бинома Ньютона 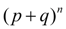, откуда и название «биномиальное распределение».

Примером является выборочный контроль качества производственных изделий, при котором отбор изделий для пробы производится по схеме случайной повторной выборки, т.е. когда проверенные изделия возвращаются в исходную партию. Тогда количество нестандартных изделий среди отобранных есть случайная величина с биномиальным законом распределения вероятностей.

Биномиальное распределение определяется двумя параметрами: n и p. Cлучайная величина, распределенная по биномиальному закону, имеет следующие основные числовые характеристики:

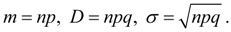(22)

Распределение Пуассона. Дискретная случайная величина Х имеет распределение Пуассона, если она имеет бесконечное счетное множество возможных значений 0, 1, 2,..., m, …, а соответствующие им вероятности определяются формулой:

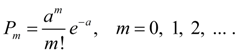(23)

Примерами случайных явлений, подчиненных закону распределения Пуассона, являются: последовательность радиоактивного распада частиц, последовательность отказов при работе сложной компьютерной системы, поток заявок на телефонной станции и многие другие.
Закон распределения Пуассона (23) зависит от одного параметра а, который одновременно является и математическим ожиданием, и дисперсией случайной величины Х, распределенной по закону Пуассона. Таким образом, для распределения Пуассона имеют место следующие основные числовые характеристики:

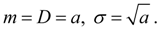(24)

Геометрическое распределение. Дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2,..., m, …, а вероятности этих значений:

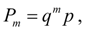(25)

где 0 < p < 1, q = 1 – p; m = 0, 1, 2,....

Вероятности Рm для последовательных значений m образуют геометрическую прогрессию с первым членом р и знаменателем q, откуда и название «геометрическое распределение».

В качестве примера рассмотрим стрельбу по некоторой цели до первого попадания, причем вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов и сохраняет постоянное значение р (0 < p < 1). Тогда количество произведенных выстрелов будет случайной величиной с геометрическим распределением вероятностей.

Геометрическое распределение определяется одним параметром р. Cлучайная величина, подчиненная геометрическому закону распределения, имеет следующие основные числовые характеристики:

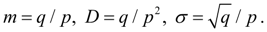(26)

Гипергеометрическое распределение. Дискретная случайная величина Х имеет гипергеометрическое распределение с параметрами a, b, n, если ее возможные значения 0, 1, 2,..., m, …, а имеют вероятности:

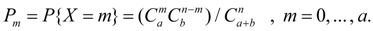(27)

Гипергеометрическое распределение возникает, например, когда из урны, содержащей а черных и b белых шаров, вынимают n шаров. Случайной величиной, подчиненной гипергеометрическому закону распределения, является число белых шаров среди вынутых. Основные числовые характеристики этой случайной величины:

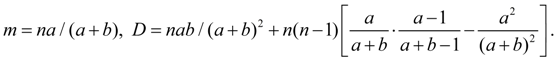(28)

Распределение непрерывных случайных величин

Непрерывное равномерное распределение — в теории вероятностей - распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна.

Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

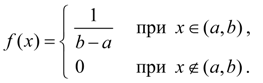(29)

Для случайной величины Х, равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x 1, x 2), лежащий внутри интервала (a, b), равна: 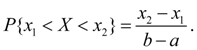(30)
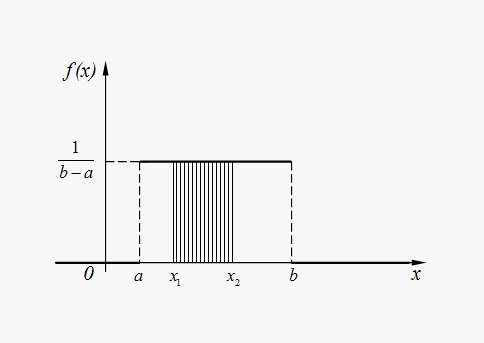
Рис. 4. График плотности равномерного распределения

Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда 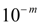, то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале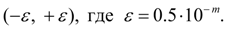

Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

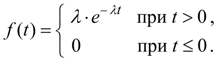(31)

График плотности распределения вероятностей (31) представлен на рис. 5.

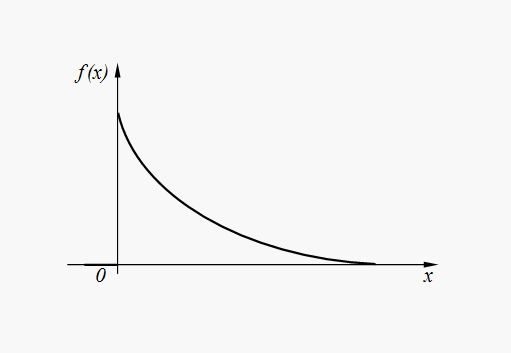
Рис. 5. График плотности показательного распределения

Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ, физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.