Глава 2 случайные блуждания и эффективные рынки

В теории финансового инвестирования нет концепции, которая имела бы такую широкую проверку и так мало доверия к себе, как «эффективные рынки». Помимо всего эта концепция является краеугольным камнем количественной теории рынка капитала, и последние тридцать с лишним лет исследований были полностью ей подчинены. В действительности гипотеза эффективного рынка (ЕМН) уходит корнями в начало века. Она выполняет одну первейшую функцию: оправдать использование вероятностных расчетов в анализе рынков капитала. Но если рынки являются нелинейными динамическими системами, то тогда использование стандартного статистического анализа может привести к ошибочным результатам, особенно если в основе лежит модель случайных блужданий. Поэтому становится важным пересмотр тех предпосылок, которые стоят во главе угла нынешней теории рынков капитала.

Эффективные рынки представляются такими, где в сложившихся ценах уже учтена и обесценена вся публичная информация, отражена как общеэкономическая так и собственно ценовая история. Ценовой сдвиг, следовательно, происходит только тогда, когда появляется новая информация. Эффективный рынок не может быть игровым, не только потому, что в ценах отражает известную информацию, но и потому, что само по себе большое количество инвесторов обеспечивает справедливость этих цен. С этой точки зрения инвесторы предполагаются рациональными: они знают в совокупности, какая информация важна, какая нет. Тогда после систематизирования этой информации и оценки рисков коллективное сознание рынка находит равновесную цену. В сущности ЕМН утверждает, что рынок создается ошибками многих.

Если это предположение о надежности рынка, обусловленной большим количеством инвесторов, истинно, то тогда сегодняшнее изменение цены зависит только от сегодняшних неожиданных новостей. Вчерашние новости недолго остаются значимыми, и сегодняшние прибыли не имеют отношения

ко вчерашним; прибыли в этом смысле независимы. А если это так, то, следовательно, они являются случайными переменными и следуют случайному блужданию. Если накоплено достаточно большое количество ценовых изменений, то в пределе (когда число наблюдений приближается к бесконечности) их вероятностное распределение становится нормальным. Это предположение о нормальности распределения прибылей открывает дорогу к несметному количеству статистических тестов и методов моделирования, которые могут дать оптимальные решения в качестве руководства к действию.

Эта версия ЕМН, основанная на случайном блуждании, во многих отношениях ограничена. Рыночная эффективность не подразумевает с необходимостью случайное блуждание, но случайное блуждание подразумевает рыночную эффективность. Следовательно, предположение о том, что прибыли нормально распределены, непременно подразумевается эффективными рынками. Однако существует глубоко укоренившееся предположение о независимости прибылей. Большинство тестов ЕМН проверяют также версию о случайном блуждании. Кроме того, в любом варианте ЕМН утверждает, что прошлая информация не влияет на рыночную активность, так как эта информация общеизвестна. Это предположение об относительной независимости изменений рыночных цен, во-первых, дает возможность использовать теорию случайного блуждания и далее более общие мартингальные и субмар-тингальные модели. И хотя не все версии ЕМН предполагают независимость, техника, используемая для статистических испытаний, несет в себе предположение о независимости, а

такЖО Г) ГуЩСГТВОВаИИИ КОНеЧНЫХ ДИСП^рсИЙ. СслеДС1ВИе сИИХ

особенностей версия ЕМН, основанная на случайном блуждании, считается единственной гипотезой эффективного рынка, ее неотъемлемым признаком, хотя технически это неверно.

Действительно, предположение о том, что прибыли следуют случайному блужданию, приходит на ум первым при наблюдении и статистическом анализе прибылей. Рациональные Доводы в пользу применения статистического анализа с его предположениями о независимости прибылей приходят много позже. ЕМН стала результатом накопления в этом процессе Рационализации.

Любой ученый может выразить недовольство тем, что те-°Рия совершенствуется ради оправдания применяемых методов: ведь это значит ставить телегу впереди лошади— такая наука никуда не годится. Если рыночные прибыли подчиняются нормальному распределению, то имеется возможность развивать гипотезу и следствия из нее. В теории рынков капитала предположения о нормальности распределений и конечной дисперсии, так же как и основанные на них модели развивались вопреки эмпирической очевидности, которая всегда вступала в противоречие с теорией.

В этой главе мы сделаем обзор теории рынков капитала и ее истории развития. Обсуждение по необходимости будет кратким. Наша цель — показать, что если предположение о случайном блуждании цен на рынках капитала неверно, то тогда большая часть нынешней теории, эмпирических исследований и исследовательской методологии окажется подорванной в своей предполагаемой полезности. На смену старым методам должны прийти новые, которые не предполагают независимости, нормальности или конечных дисперсий. Эти новые методы должны включать фракталы и нелинейную динамику, которые, будучи примененными к реальным данным, демонстрируют гораздо большую результативность. Ко всему прочему нелинейная парадигма должна допустить в теорию рынков концепцию «долговременной памяти»: событие может влиять на рынки долго, возможно — бесконечное время в будущем. Нынешняя линейная парадигма допускает лишь возможность короткой памяти, в лучшем случае — в субмартингальной форме.

РАЗВИТИЕ ГИПОТЕЗЫ ЭФФЕКТИВНОГО РЫНКА

Оригинальная работа, использующая статистические методы для анализа прибылей, была опубликована в 1900 г. Луи Ва-шелье, который применил к акциям, облигациям, фьючерсам и опционам методы, созданные для анализа азартных игр. Статья Вашелье стала работой пионерского предвидения, намного опередившей время. В числе ее достоинств было открытие того факта, что процесс случайных блужданий (позже формализованный Винером) является броуновским движением. Эйнштейн переоткрыл эту связь десятилетием позже.

Башелье первым предложил графическое изображение опционных выигрышей — ныне знакомую всем линию в форме угла, а также соответствующие графики для страдлов и других опционных стратегий. Однако за недостатком эмпирических данных утверждение Башелье о том, что рыночные прибыли являются независимыми, идентично распределенными (IID) случайными величинами, осталось нереализованным в практическом анализе.

Диссертация Башелье была революционной, но в значительной степени она была проигнорирована и забыта. Применение статистического анализа к рынкам увяло (за исключением работ Холбрука Уоркинга и Альфреда Коулса в 30-х годах), и так продолжалось до конца 40-х годов. Зато потом прогресс был бурным. Большинство работ, которые стали основой ЕМН, были собраны Кутнером (Cootner) в его классическом томе (1964b) под названием «Случайный характер цен фондового рынка», впервые опубликованном в 1964 г. Антология Кутнера, ставшая основой для первой «золотой поры» количественного анализа, рассматривала непосредственно рыночные характеристики, но не затрагивала теории портфеля. В нее не была включена работа Марковица, Тобина и Шарпа, которая также появилась в этот период. В книге содержатся логические обоснования того, что было формализовано Фамэ как ЕМН в 60-х годах.

В течение десятилетий, с 1920-х по 1940-е годы, в рыночном анализе доминировали фундаменталисты (последователи Грэхема и Додда) и техники (или технические аналитики, последователи Маги). В 1950-е годы добавилась третья группа — количественников (или количественных аналитиков, последователей Башелье).

По своей природе количественники были ближе к фундаменталистам, чем к техникам, потому что предполагали, что инвесторы рациональны — это было нечто вроде самоподтверждения. Техники же полагали, что рынком правит «животный дух» — как сказал лорд Кейнс.

Предубежденность против технического анализа отражена в статье Робертса (Roberts, 1964) в кутнеровском томе. Роберте призывает к широчайшему использованию статистического анализа, основанного на работах Кендалла (Kendall, 1964), который сказал: «... изменения в ценах на бумаги ведут себя так, как если бы они порождались рулеткой, для которой каждое выпадение статистически независимо от прошлой истории и отношения частот достаточно устойчивы во времени». Роберте далее утверждает, что «модель изменений настойчиво требует независимости», а вероятности «должны быть устойчивы во времени». Логическим обоснованием для принятия случайной модели служит следующее соображение: если рынок был несовершенной рулеткой, то «люди должны были бы заметить это и своими действиями изменить его». Допуская это положение, Роберте однако не соглашается с ним. Его статья призывает к дальнейшим исследованиям.

Утверждение о том, что цены акций следуют случайному блужданию, было формализовано Осборном (Osborne, 1964) в его теоретической статье о броуновском движении. Осборн предложил модель, в которой изменения цен на фондовом рынке эквивалентны движению частицы в жидкости, обычно именуемому броуновским движением. Это сделано путем выдвижения ряда предположений и формальных выводов, приводящих к требуемому результату.

Первые два предположения касаются минимальных ценовых движений (| доллара) и того факта, что количество ежедневных сделок конечно и не существенно. Однако далее Осборн переходит к некоторым предположениям, принимающим во внимание инвесторское ощущение ценности. Таким образом, третье предположение гласит, что «цена и ценность связаны» и что это отношение есть первейший определитель рыночных прибылей. Предположение 4 говорит, что в случае двух ценных бумаг с различной ожидаемой прибылью логичным решением будет выбор акций с более высокой ожидаемой прибылью. «Ожидаемая прибыль» есть сумма вероятностей прибылей, слагающих суммарную прибыль. Вероятности дополняются до единицы, так что ожидаемая прибыль есть вероятностно взвешенная прибыль, или ожидаемая величина случайной переменной.

Предположение 5 утверждает, что покупатели и продав-тты «не расположены к торговле пока нет равенства возможностей для дохода». Другими словами, покупатель не может иметь преимущества перед продавцом и наоборот, если сделка совершена. Осборн говорит, что предположение 5 является следствием предположений 3 и 4.

Таким образом, общее равновесие цен (предположение 5) имеет место потому, что инвесторы внимательнейшим образом следят за тем, чтобы уплатить верную цену за ценность (предположение 3) и, будучи поставлены перед выбором между двумя переменными с некоторыми ожидаемыми величинами, выберут ту, что сулит большую прибыль (предположение 4); в результате продавец и покупатель всегда находят взаимовыгодную цену. Другими словами, поскольку инвесторы способны рационально сравнить цену и стоимость, они будут стоять на равновесной цене, основанной на доступной в данное время информации. Таким образом, последовательность ценовых изменений независима, так как цена уже приравнена к доступной информации.

Предположение 7 Осборна является кульминацией предположений 3-6. В действительности оно является заключением и утверждает, что так как ценовые изменения независимы (т. е. они представляют собой случайные блуждания), следует ожидать нормального распределения этих изменений с устойчивым средним значением и конечной дисперсией. Это не что иное как следствие центральной предельной теоремы теории вероятностей, или закона больших чисел. Эта теорема гласит, что выборка независимых идентично распределенных случайных переменных (1ГО) будет нормально распределенной, если эта выборка достаточно велика.

Несмотря на тот факт, что мы ставим под вопрос логику Осборна, не следует умалять его достижения. Осборн собрал коллекцию разных концепций, относящихся к теории случайных блужданий, которые в конечном счете оправдывают применение вероятностных расчетов. В сущности, эта группа исследователей знала, что статистический анализ предлагает огромное количество исследовательских методов и моделей. Эти инструменты, однако, ограничены лежащими в их основе предположениями. Главным было следующее: изучаемый объект должен быть независимой идентично распределенной случайной переменной. Таким образом, постулировалось, что поскольку фондовый рынок и другие рынки капитала пред-гтяиттсткуг собой большие системы с большим число:.: степеней свободы (или — инвесторов), текущие цены должны отражать информацию, уже имеющуюся в распоряжении каждого. Изменения в цене должны происходить только по возникновении новой неожиданной информации.

Отцы-основатели теории рынка капитала были хорошо осведомлены об этих упрощающих предположениях и их значении. Они не пытались минимизировать влияние этих предположений на теорию, однако чувствовали их существенное Влияние на полезность модели, особенно в отношении принятого допущения об инвесторском поведении. Концепция рационального инвестора стала ключевой предпосылкой для гипотезы эффективного рынка (ЕМН).

Как мы видели, Осборн уже коснулся этой концепции. Он говорил, что инвесторы оценивают акции, основываясь на их ожидаемой стоимости (или ожидаемой прибыли), которая есть вероятностно взвешенное среднее ожидаемых прибылей. Предполагалось, что инвесторы кладут в основу своих расчетов субъективно оцененные вероятности и манипулируют с ними рационально и непредубежденно.

Предположим, например, что инвестор видит три возможных экономических сценария: положительный рост, отсутствие роста и отрицательный рост. В случае положительного роста инвестор полагает, что рынок вырастет на 12%. При отсутствии роста рынок упадет на 1%. Если же экономика пойдет на спад, рынок упадет на 8%. Инвестор производит экономический анализ и решает, что сценарий роста имеет вероятность 60%, отсутствие роста —30% и спад—10%. Тогда ожидаемая прибыль будет:

0.6 * 12% + 0.3 * (-1%) + 0.1 * (-8%) = 6.1%

Таким способом принимают решения многие инвесторы. Они оценивают вероятности и возможности выигрыша по различным сценариям, но не обязательно принимают окончательное решение исходя из них.

Позже мы обсудим некоторые исследования в области принятия решений человеком, но сейчас в качестве примера возьмем лотерею. Ожидаемая прибыль лотерей типично отрицательна. Эта действительно так — иначе лотереи не приносили бы прибыль их организаторам. Но миллионы людей играют в лотерею, хотя пн один " рациональный инв^тор» w гтятт бы этого делать. Лотерейные игроки, очевидно, чувствуют, что вероятность большого выигрыша возмещает риск небольшой потери, даже если вероятности им не благоприятствуют. Это не «рациональная», но тем не менее человеческая природа.

Фамэ (Fama, 1965а) окончательно формализовал эти наблюдения в виде гипотезы эффективного рынка (ЕМН), которая утверждает, что рынок является мартингалом, или «справедливой игрой»; это означает, что информация не может быть использована для выигрыша на торговой площадке. ЕМН подобна предположению 5 Осборна. В ее чистой форме ЕМН не требует независимости во времени или принятия только IID наблюдений. Однако модель случайного блуждания исходит из этих предположений. Если прибыли случайны, то тогда рынки эффективны. Обратное утверждение, однако может не быть истинным.

Эта концепция эффективных рынков в итоге разрослась до атаки как на фундаментальный, так и на технический анализ. Теперь в фокусе оказалось положение о том, что прошлая ценовая информация не отражается на будущих ценах. Лори и Гамильтон (Lorie, Hamilton, 1973) писали в 1973 г. в своем великолепном обзоре:

«Утверждение о том, что рынок эффективен, много сильнее, чем утверждение, что последовательные изменения в ценах акций не зависят одно от другого. Последнее утверждение— легкая форма гипотезы эффективного рынка—просто говорит, что текущие цены акций полностью отражают все что скрыто в исторической последовательности цен, так что знание этой последовательности не имеет значения при формировании ожиданий касательно цен будущих. Утверждение о том, что рынок эффективен, подразумевает, что текущие цены отражают и заключают в себе не только все, что скрыто в исторической последовательности цен, но также все, что можно было узнать о компаниях, чьи акции находятся в обращении... это доказывает бесплодность усилий заработать сверхприбыль путем анализа всей публичной информации».

Эта атака на фундаментальный анализ вообще была неприемлема для сообщества инвесторов — и она разделила ЕМН на «слабую» и «сильную» формы. Сильная форма утверждала, что фундаментальный анализ был бесполезной деятельностью, потому что цены уже отразили «все, что познаваемо», или всю публичную или частную (из информированных игт< -«чннкок) информацию. В качестве компромисса была выдвинута «полусильная» форма.

В соответствии с полусильной формой ЕМН цены отражают всю «публичную» информацию. Аналитики ценных бумаг, используя технику Грэхема—Додда, выводят формулу стоимости ценной бумаги, основанную на информации, которая Доступна всем инвесторам. Большое число независимых оценок дает в результате «справедливую» стоимость для этого агрегированного рынка. Аналитики, таким образом, становятся причиной рыночной эффективности. Фундаменталисты формируют справедливую цену путем консенсуса.

Полусильная форма ЕМН была намного более приемлема Для сообщества инвесторов, потому что она гласила, что рын-Ки эффективны вследствие анализа ценных бумаг, а не независимо от анализа. К тому же, полусильная форма подразумевала, что изменения в ценах акций случайны, так как подвержены внешним по отношению к самому временному ряду, воздействиям. Следовательно, ценовые изменения случайны не потому, что сам рынок является «игрой в кости», но вслед- j ствие оценки изменений в положении компании, обусловлен-! ных микро- и макроэкономическими условиями. В середине! 1970-х годов полусильная версия ЕМН была общепринятой теорией. Говоря о ЕМН, подразумевали именно ее. В даль-, нейшем мы всегда будем иметь в виду полусильную версию ЕМН, которая утверждает, что рынки.эффективны потому, '. что отражают всю публичную информацию. Слабая форма эффективного рынка есть такая, где ценовые изменения независимы и могут быть случайным блужданием.

Академическое сообщество претерпело тридцатилетний парадигмальный сдвиг — от «животного духа» Кейнсадо «рационального инвестора» и ЕМН. К 1970-му году академическое сообщество в целом приняло ЕМН (сообщество инвесторов сделало это несколькими годами позже) и то, что Кан (Kuhn, 1962) назвал «нормальной наукой», было взято на вооружение теорией финансов. В части 3 мы обсудим основные труды, которые призваны были доказать правдоподобие

ЕМН.

СОВРЕМЕННАЯ ТЕОРИЯ ПОРТФЕЛЯ

Тем временем уже стала разрабатываться новая теория портфеля (МРТ). Марковиц (Markwitz, 1952) определил меру как, ттисперсию распределения возможных прибылей риска порт- і феля. Формально дисперсия совокупности определяется еле-! дующей формулой:

(2.1)

где а2—дисперсия, т^ — среднее значение прибыли, ^ — наблюдаемая прибыль.

В пределе дисперсия должна измерять рассеяние возможных прибылей относительно среднего значения прибыли. Квадратный корень из дисперсии, или стандартное отклонение, измеряет вероятную величину отклонения прибыли от своего среднего значения. Если мы используем концепцию

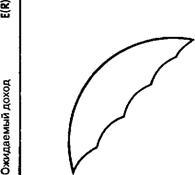
ожидаемой прибыли Осборна, мы сможем оценить вероятность отклонения реальной прибыли от среднего. Чем шире рассеяние, тем больше будет стандартное отклонение, и тем рискованнее капитал. Само по себе использование дисперсии требует того, чтобы прибыли были нормально распределены. Однако, если фондовые прибыли следуют случайному блужданию, и случайные переменные являются независимыми идентично распределенными (ГШ), то тогда по утверждению центральной предельной теоремы (или закону больших чисел) распределение должно быть нормальным и дисперсия — конечной. Инвесторы, таким образом, должны располагать портфелем с наивысшей ожидаемой прибылью для определенного уровня риска. Инвесторы предполагаются не склонными к риску. Этот подход стал известен как «эффективность по среднему/дисперсии». Кривая, представленная на рис. 2.1, была названа «эффективной границей», поскольку эта замкнутая линия заключает внутри себя портфели с наивысшими уровнями ожидаемых доходов для данных уровней риска, или стандартного отклонения. Инвесторы должны предпочитать эти оптимальные портфели, основанные на модели рационального инвестора.

Эти концепции были расширены Шарпом (БЬагре, 1964), Литнером (Ьи; пег, 1965) и Моссином (Мозэт, 1966) и вылились в известную модель оценки капитальных активов (САРМ), — это название было придумано Шарпом. САРМ объединила гипотезу эффективного рынка (ЕМН) и математическую модель теории портфеля Марковица в модели инве-сторского поведения, основанной на рациональных ожиданиях в рямкяу общрй концепции рявчоврсия В частности оня

предполагает, что инвесторы имеют однородные ожидания, касающиеся прибыли. Следовательно, они одинаковым образом интерпретируют информацию. САРМ была выдающимся достижением трех независимых исследователей.

Ввиду того что САРМ широко обсуждалась в литературе, наше рассмотрение здесь будет ограничено в основном аспектами, которые соотносятся с предпосылкой о том, что необходима новая парадигма. САРМ начинается с предположения, что мы живем в мире, свободном от издержек на совершение сделок, комиссионных и налогов. Эти упрощающие предположения были необходимы для отделения инвесторского поведения от ограничений, накладываемых обществом. Физики часто поступают подобным образом, например предполагая

Риск

Рис. 2.1. Эффективная граница.

отсутствующим трение. Далее САРМ говорит, что каждый может заимствовать средства и давать взаймы на безрисковой ставке процента, которая понимается обычно как 90-дневная казначейская ставка. В итоге это предполагает, что все инвесторы стремятся к средне-дисперсной эффективности Мар-ковица. т е желают им^тъ портфель с наивысшим уппр н«*м ожидаемой прибыли для заданного уровня риска и в целом не любят рисковать. Риск снова определен как стандартное отклонение прибыли. Инвесторы, таким образом, рациональны в смысле Осборна и Марковица.

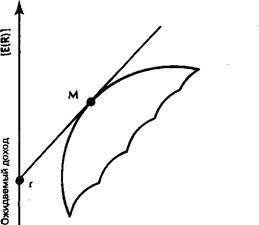
Основываясь на этих предположениях, САРМ продолжает делать заключения о поведении инвесторов. Во-первых, оптимальным портфелем для всех инвесторов должна быть некоторая комбинация рыночного портфеля (все рисковые активы капитализационно взвешены) и безрисковых активов. Этот тип портфеля показан на рис. 2.2. Линия рынка капитала касается эффективной границы рыночного портфеля (М), и точка ее пересечения с осью У есть безрисковая ставка процента (г). Уровень риска можно менять путем добавления бе-

Риск

Рис. 2.2. Линия рынка капитала.

зрисковых активов, чтобы уменьшить стандартное отклонение портфеля, или путем получения кредитов по этой ставке, чтобы заемными средствами воздействовать на рыночный портфель. Портфели, которые лежат на этой прямой, называются лежащими на линии рынка капитала (CML — Capital Market Line) и они количественно преобладают над портфелями, лежащими на эффективной границе, — инвесторы предпочитают такие портфели всем другим. Добавим, что инвесторы не компенсируют убытков от нерыночного риска, поскольку оптимальные портфели лежат на CML. Эта модель также утверждает, что активы с более высоким риском должны иметь более высокие прибыли. Так как риск теперь отнесен к рыночному портфелю, используется линейная мера чувствительности риска ценной бумаги к рыночному риску. Эта линейная МеРа носит название бета. Если все рисковые активы разместить в координатах «бета — ожидаемая прибыль», результатом будет прямая линия, пересекающая ось У на безриско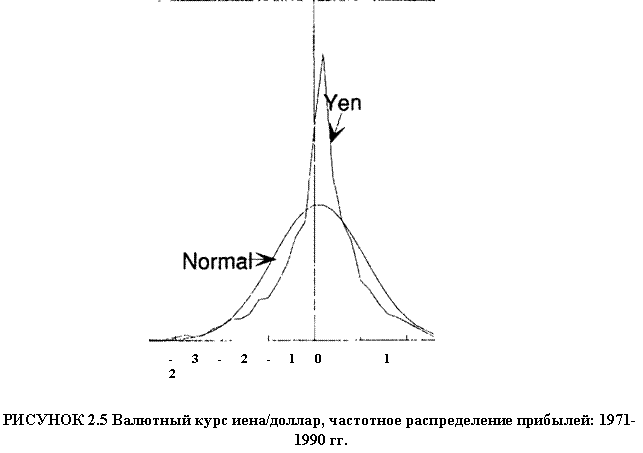

вой ставке процента и проходящая через рыночный портфель. Она называется линией рынка ценных бумаг (SML — Security Market Line). Ее график показан на рис. 2.3.

Это короткое и по необходимости неполное обсуждение САРМ призвано показать сущностную зависимость модели от стандартного отклонения как меры риска По смыслу С! ДРМ требует эффективного рынка и нормального или логнормаль-ного распределения прибыли, поскольку дисперсия предполагается конечной. Предлагая практические количественные методы, САРМ остается стандартом для любой новой модели инвесторского поведения. Теория портфеля Марковица объяснила, почему диверсификация уменьшает риск. САРМ объяснила, каким образом должны были бы вести себя инвесторы, если они рациональны. Практики вынуждены были согласиться, что предположения, лежащие в основе САРМ, хотя и являются упрощающими существо дела, тем не менее не умаляют полезности модели. ЕМН стала широко применяться в качестве логического обоснования для использования гаус-совского логнормального распределения прибыли. Борьба за признание модели, возможно, заставила этих ранних поборников количественных методов настаивать на том, что ЕМН является истиной. Объединение ЕМН и САРМ и ее модификаций стало общеизвестно как новая теория портфеля (МРТ — Modern Portfolio Theory). Все та же борьба за признание, вероятно, стала причиной того, что обсуждение нежелательных подробностей было отодвинуто на задний план.

ЕМН подкрепила МРТ, и дисперсия, и стандартное отклонение были приняты сообществом инвесторов как истинные меры риска. Повторим снова, ранние основатели теории рынков капитала были хорошо осведомлены об этих предположениях и их ограниченности. Самуэльсон, Шарп и Фаме (среди других) опубликовали работы, модифицирующие МРТ для не нормальных распределений. Эмпирические данные 60-х годов из статьи Мандельброта (1964) свидетельствовали в пользу устойчивого распределения Парето; в этой статье он показал, что поскольку прибыли не нормально распределены, имеется необходимость для возможной ревизии ЕМН и МРТ. (Мы рассмотрим устойчивое распределение Парето в деталях в части 2, где будем знакомиться с фракталами.) Было уже накоплено много фактов, свидетельствующих о том, что прибыли не следуют нормальному распределению, в то время когда Шарп (Sharpe, 1970) и Фамэ и Миллер (Fame, Miller, 1972) опубликовали свои работы; обе книги содержат разделы, в которых говорится о необходимости модификации стандартной теории портфеля с учетом устойчивого распределения Парето.

В 1970-х годах эта дискуссия утихла, если не считать отдельных академических статей, среди которых выделяется пч^г> та Ролла (Roll. 1977) Развитие экономики финансов продолжалось на основе слабой формы ЕМН и ее предположении о том, что ценовые изменения независимы. Вдобавок, нормальное распределение с его гауссовским предположением о независимости стало общепринятым в моделировании. Применения эконометрики к рынкам капитала стали более комплексными, так как ЕМН получила широкое признание и все меньше ставилась под вопрос. Главными достижениями были модель расчета цен опционов Блэка и Шоулса (Black, Scholes, 1973) и арбитражная ценовая теория (APT — Arbitrage Pricing Theory) Росса (Ross, 1976). APT является 0°лее общей ценовой моделью, чем САРМ; она предполагает, ЧТо ценовые изменения происходят в результате неожиданного изменения факторов и, следовательно, может манипулировать с нелинейными отношениями. Однако практически для инструментального оснащения APT была использована стандартная эконометрика (включая предположение о конечной дисперсии). APT стала альтернативной теоретической ценовой моделью, которая не зависела от квадратических функций полезности.

В последние годы теоретические модели стали появляться реже. Работы 1980-х годов были сосредоточены на эмпирических исследованиях и приложениях уже существующих моделей. Единственное теоретическое достижение, получившее широкое признание в последние годы, постулировало, что рыночная волатильность изменяется во времени. Это означает, что волатильность зависима от своих предыдущих уровней. Эта модель вела свое происхождение от авторегрессионных условных гетероскедастических (ARCH) моделей Ингла (Engle, 1982). От его оригинальной работы берут свое начало многие разновидности моделей, основанных на ARCH. Однако все они исходят из предположения о кратковременной памяти в исследуемых процессах, а также — в той или форме — о рыночной эффективности.

ВЫВОДЫ

В своем настоящем виде теория рынков капитала основывается на следующих ключевых концепциях:

Рациональные инвесторы.

Инвесторы желают среднедисперсной эффективности, j Они оценивают потенциальную прибыль методом вероят-> ностного взвешивания, который дает ожидаемые прибыли^ Риск измеряется как стандартное отклонение прибылей! Инвесторы предпочитают активы, которые дают наивысшую ожидаемую прибыль при заданном уровне риска. Они не любят рисковать.

Эффективный рынок.

Цены отражают всю публичную информацию. Изменения в ценах не соотносятся между собой, разве что для очень коротких временных зависимостей, которые быстро дис-сипируют. Стоимость определяется консенсусом большого количества фундаментальных аналитиков.

Выводы

3. Случайные блуждания.

Вследствие двух названных выше концепций цены следуют случайному блужданию. Следовательно, вероятностное распределение приблизительно нормально или логнор-мально. Эта приблизительность означает, как минимум, что распределение прибылей имеет конечную среднюю величину и дисперсию.

Этот перечень указывает на то, что теория рынков капитала существенно зависит от нормальности распределения прибылей. Эмпирические исследования пытались доказать это гауссовское предположение, но часто доставляли противоположные результаты. Мы обсудим некоторые из этих работ в следующей главе.

На протяжении 1950-х и 1960-х годов влияние предположений о нормальности стало понятным. Отличное от нормального распределение прибыли всегда считалось хотя и нежелательным, но возможным. Однако в течение 1970-х и частично 1980-х годов ЕМН была, в целом, признанным фактом. Поскольку в 1980-х годах было выпущено большое число магистров экономики управления (MBА), возникло ощущение того, что будто бы доказана истинность ЕМН. Всеобщее признание ЕМН может проистекать также из тех усилий, которые были предприняты академиками в 1960-х и ранних 1970-х годах для признания их теорий. Здоровый скептицизм не возымел действия, как это, впрочем, случалось во все времена.

Были проигнорированы две возможности: предположить, что различные рынки и ценные бумаги связаны друг с другом и что мпдрп*. пяциачцттт> ттг> гп инвестора нереалистична. Как мы увидим, люди не ведут себя таким образом, который предписывает им теория рациональных ожиданий. То обстоятельство, что инвесторы могут не знать, как нужно интерпретировать всю известную информацию, и реагируют на тренды, тем самым включая прошлую информацию в свою текущую Деятельность, рассматривалось как излишнее усложнение, которое должно быть отброшено, как это делается с транзак-Ционными издержками и налогами. Однако понимание того, люди интерпретируют информацию, может быть более Важным, чем это считалось ранее, — даже если математика не °чень при этом строга. В частности, это касается нынешней теории рынков капитала, основанной на линейном подходе к °бщ, еству. Если следовать ему, то люди, получая информацию, немедленно ее используют, и ценные бумаги держатся на своих бета, которые представляют собой наклон линий регрессии, между дополнительным доходом по активу и по рыночному; портфелю. Эта линейная парадигма построена в предположении о нормальности распределений. Однако мы увидим, что. люди и природа в целом — нелинейны. В отличие от предположения о несущественности влияния налогов, предположение О: рациональности инвесторов изменяет саму природу этой не-, линейной системы. Вот почему линейная парадигма, несмо- | тря на ее простоту и концептуальную элегантность, обладает і серьезным недостатком. В следующей главе мы протестируем • линейную парадигму и посмотрим, что же это дает.