Случайные величины. Нахождение вероятности события B (в серии n независимых испытаний событие А произошло m раз) по формуле Бернулли при больших затруднителен

Формула Пуассона

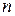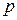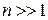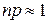Нахождение вероятности события B (в серии n независимых испытаний событие А произошло m раз) по формуле Бернулли при больших затруднителен. Но в случае малой вероятности успеха, можно оценить вероятность B следующим образом: если и , то 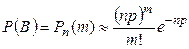. Обозначив , получим:

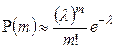. (11)

Параметр 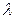равен среднему числу успехов в серии из 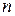испытаний, т.е. ожидаемому числу успехов, где под 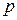понимается частота успеха.

Случайные величины

Случайная величина – переменная величина, которая принимает значения в зависимости от исходов испытания, т.е. случайным образом. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены, [1, с. 57].

Дискретная случайная величина – случайная величина, принимающая конечное или счётное множество значений.

Непрерывная случайная величина – случайная величина, принимающая значения из некоторого промежутка.

Закон распределения дискретной случайной величины – соответствие между значениями 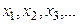этой величины и их вероятностями 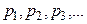. Закон распределения дискретной случайной величины задаётся таблично или аналитически:

1) табличное задание (табл.1)

Таблица 1 – Закон распределения дискретной случайной величины Х

Х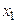
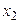
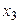
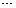
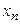
Р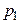

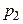
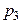
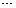
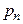
2) аналитическое:

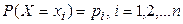, при этом 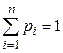, [3, c. 52].