
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Простейший поток заявок
|
|
Как правило, входящие и выходящие потоки требований являются нерегулярными, случайными. Они могут описываться различными вероятностными распределениями.
Мы рассмотрим так называемые простейшие (пуассоновские) потоки.
Сопоставим каждому интервалу времени длины  вероятностное пространство, обладающее следующими свойствами.
вероятностное пространство, обладающее следующими свойствами.
Пространство элементарных исходов 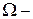 это множество
это множество  =
=  . Каждому элементарному исходу
. Каждому элементарному исходу 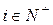 поставлена в соответствие вероятность
поставлена в соответствие вероятность  ,
, 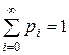 .
.
Содержательный смысл элементарного исхода таков: 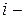 число заявок, поступивших в систему (покинувших систему) за время
число заявок, поступивших в систему (покинувших систему) за время  . Далее для определенности будем рассматривать входные потоки заявок.
. Далее для определенности будем рассматривать входные потоки заявок.
Поток заявок называют простейшим, если выполнены условия, которые называются стационарностью, ординарностью, отсутствием последействия.
Постулируем, что вероятности  ,
, 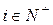 , зависят только от длины
, зависят только от длины  интервала времени и не зависят от того, где именно на оси времени расположен этот интервал. Положим также, что математическое ожидание случайной величины
интервала времени и не зависят от того, где именно на оси времени расположен этот интервал. Положим также, что математическое ожидание случайной величины  с законом распределения
с законом распределения 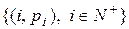 (
( - число заявок, поступивших в систему за время
- число заявок, поступивших в систему за время  ) равно
) равно  , где
, где  константа. Эту константу называют еще средней плотностью данного потока заявок (средним числом заявок, поступающим в систему в единицу времени). Далее перейдем к обозначениям
константа. Эту константу называют еще средней плотностью данного потока заявок (средним числом заявок, поступающим в систему в единицу времени). Далее перейдем к обозначениям 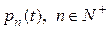
Описанное свойство называют стационарностью потока заявок.
Рассмотрим бесконечно малый промежуток времени  . Постулируем, что вероятность
. Постулируем, что вероятность  есть действительное число, вероятность
есть действительное число, вероятность 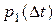 есть бесконечно малая того же порядка, что
есть бесконечно малая того же порядка, что  , а остальные вероятности
, а остальные вероятности 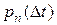 ,
,  есть бесконечно малые высших порядков в сравнении
есть бесконечно малые высших порядков в сравнении  . Другими словами, мы сужаем пространство элементарных исходов до двух исходов: за бесконечно малое время
. Другими словами, мы сужаем пространство элементарных исходов до двух исходов: за бесконечно малое время  в систему либо вовсе не поступают заявки, либо может поступить одна заявка.
в систему либо вовсе не поступают заявки, либо может поступить одна заявка.
Тогда  +
+ 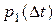 = 1. Кроме того
= 1. Кроме того
 =
= 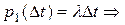
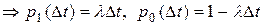 .
.
Это свойство называют ординарностью потока заявок.
Объясним теперь, что такое отсутствие последействия.
Рассмотрим на оси времени два непересекающихся интервала длины  . В качестве пространства элементарных исходов введем множество упорядоченных пар
. В качестве пространства элементарных исходов введем множество упорядоченных пар  . Будем говорить, что имеет место отсутствие последействия, если вероятность исхода
. Будем говорить, что имеет место отсутствие последействия, если вероятность исхода  равна произведению
равна произведению  . Отсутствие последействия предполагает взаимную независимость поступления заявок в непересекающихся промежутках времени.
. Отсутствие последействия предполагает взаимную независимость поступления заявок в непересекающихся промежутках времени.
Из условия отсутствия последействия, следует, что
 . (1)
. (1)
Кроме того
 (2)
(2)
Обратимся к равенству 1, устремив  к 0.
к 0.
 ;
;
 , тогда
, тогда
 . (3)
. (3)
Итак, вероятность 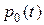 , как функция времени t, есть дифференцируемая функция и
, как функция времени t, есть дифференцируемая функция и  .
.
С начальным условием 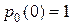 имеем такое решение:
имеем такое решение:
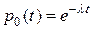 . (4)
. (4)
Рассмотрим простейший поток заявок и предположим, что элементарный исход - это время между двумя последовательными поступлениями заявок. Поставим в соответствие каждому элементарному исходу число  длину этого интервала времени. Покажем, что так определена непрерывная случайная величина
длину этого интервала времени. Покажем, что так определена непрерывная случайная величина 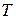 . Для этого достаточно показать, что у величины
. Для этого достаточно показать, что у величины 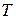 существует дифференцируемая функция распределения.
существует дифференцируемая функция распределения.
 – это вероятность того, что время между двумя последовательными заявками не меньше t. Эта вероятность равна, очевидно, вероятности того, что за время t в систему не поступит ни одной заявки. Учитывая, что поток простейший, получаем:
– это вероятность того, что время между двумя последовательными заявками не меньше t. Эта вероятность равна, очевидно, вероятности того, что за время t в систему не поступит ни одной заявки. Учитывая, что поток простейший, получаем: 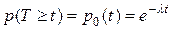 . Тогда,
. Тогда,
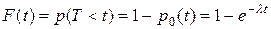 . (5)
. (5)
Таким образом, случайная величина T имеет показательное распределение с параметром 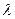 . Математическое ожидание случайной величины Т равно
. Математическое ожидание случайной величины Т равно  . Смысл этой величины таков: если
. Смысл этой величины таков: если  – среднее число заявок за единицу времени, то
– среднее число заявок за единицу времени, то  – среднее время между двумя последовательными заявками.
– среднее время между двумя последовательными заявками.
Экспоненциальное распределение обладает одним уникальным свойством, которое называется отсутствием памяти. Оно заключается в следующем. Пусть со времени поступления заявки прошло время 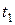 . Тогда вероятность того, что до поступления следующей заявки пройдет еще время, не меньшее t, не зависит от величины
. Тогда вероятность того, что до поступления следующей заявки пройдет еще время, не меньшее t, не зависит от величины 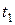 ,
,
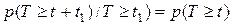 (6)
(6)
Действительно, по теореме умножения вероятностей:
 =
=  =
= 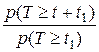 =
=
= 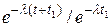 =
= 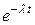 =
=  .
.
Мы показали, что если поток требований – простейший, то время между двумя заявками распределено по показательному закону. Можно показать и обратное: если время между поступлениями заявок имеем показательное распределение, то поток требований обладает свойствами стационарности, ординарности и отсутствием последействия.
Выведем теперь формулы для подсчета вероятностей 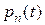 . Воспользуемся свойствами ординарности и отсутствия последействия. Если
. Воспользуемся свойствами ординарности и отсутствия последействия. Если  бесконечно малый интервал времени, то вероятность
бесконечно малый интервал времени, то вероятность  – это вероятность суммы двух несовместных событий: или n требований поступают в систему за время t и за время
– это вероятность суммы двух несовместных событий: или n требований поступают в систему за время t и за время  не поступает ни одного требования, или за время t в систему поступят
не поступает ни одного требования, или за время t в систему поступят  заявок, а за время
заявок, а за время  поступит еще одна заявка. Тогда
поступит еще одна заявка. Тогда
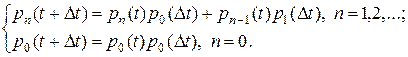
Так как 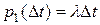 ,
, 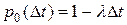 , то
, то 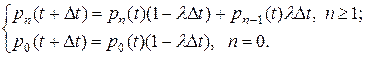
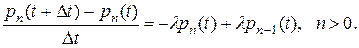
Положим  , тогда
, тогда
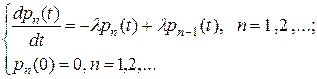
При этом 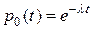
Решение этой системы дифференциальных уравнений таково:
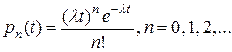 (7)
(7)
Вероятности 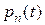 - это пуассоновские вероятности с параметром
- это пуассоновские вероятности с параметром  .
.
Параметры закона: математическое ожидание числа требований, поступавших в систему за время t, равно  ; дисперсия числа требований равна
; дисперсия числа требований равна  .
.
Справедливо следующее утверждение: если число требований, поступивших в систему за время t, имеет пуассоновское распределение с параметром  , то время между последовательными поступлениями заявок распределено по показательному закону с параметром
, то время между последовательными поступлениями заявок распределено по показательному закону с параметром  . Обратно: если интервал времени между моментами поступления заявок имеет показательное распределение с параметром
. Обратно: если интервал времени между моментами поступления заявок имеет показательное распределение с параметром  (средним значением
(средним значением  ), то число поступлений заявок в интервале длины t единиц времени имеет пуассоновское распределение с параметром
), то число поступлений заявок в интервале длины t единиц времени имеет пуассоновское распределение с параметром  (средним значением
(средним значением  ).
).
Отметим, что объединение двух независимых простейших потоков с параметрами 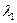 и
и 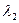 снова дает простейший поток с параметром
снова дает простейший поток с параметром  . Так получается вследствие того, что число заявок результирующего потока, поступающих в единицу времени, есть сумма двух независимых случайных величин, имеющих распределение Пуассона с параметрами
. Так получается вследствие того, что число заявок результирующего потока, поступающих в единицу времени, есть сумма двух независимых случайных величин, имеющих распределение Пуассона с параметрами  соответственно. Но такая случайная величина распределена по закону Пуассона с параметром
соответственно. Но такая случайная величина распределена по закону Пуассона с параметром  .
.