Синтез автомата по дереву управления

Проектировщик далеко не всегда может описать аналитически (или даже алгоритмически) поведение искомого автомата. Иногда проще указать «во что» перерабатывается та или иная последовательность входных букв.

Полагая, что автомат имеет ограниченное число состояний, а также может быть установлен в начальное состояние, всю информацию «стимул—реакция» можно представить в виде дерева управления.

Корнем дерева управления всегда является начальное состояние. Высота дерева h соответствует длине анализируемых вход – выходных последовательностей. Ветви 1-го яруса отображают реакции автомата на каждую из входных букв x ₁, ……., x _m, то есть на все слова длины 1. Ветви 2-го яруса — реакции автомата на все возможные слова длины 2 и т. д. По терминологии [1] рассматриваемое дерево представляет результаты многократного эксперимента над искомым автоматом.

Так возникает задача свертки дерева с целью более компактного представления модели управления в виде конечного автомата. В общем случае некоторые ветви сформированного дерева управления могут оказаться неотмеченными, что соответствует получению частичного определенного автомата.

Для однозначного восстановления автомата Мили с числом состояний не более n необходимо и достаточно иметь дерево управления высоты h 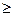2n—1.

Эта задача может быть решена путем отождествления неразличимых вершин, то есть таких вершин, из которых «растут» одинаково размеченные поддеревья. Причем высота сравниваемых поддеревьев определяется неразличимой вершиной, находящейся на верхнем (относительно других вершин) ярусе. Так, изображенное на рис. 1.1 дерево управления содержит три различимые вершины, соответствующие состояниям s ₀, s ₁, s ₂ абстрактного автомата (рис. 1.2).

Рис. 1.1. Дерево управления искомого автомата

Остальные вершины дерева, помеченные одинаковыми метками, — не различимы и поэтому подлежат отождествлению. Неразличимые вершины образуют базис на основе которого строится искомый автомат. В процессе построения графа переходов/выходов частично-определенного автомата допускается «скользящее» доопределение ветвей дерева, исходя из возможности минимизации числа неразличимых вершин.

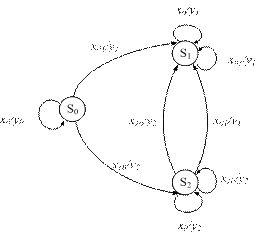
Рис. 1.2. Результат абстракт­ного синтеза

При реализации рассмотренного метода большое значение имеют следующие показатели:

— степень достижимости d — минимальная длина эксперимента,

достаточная для перевода автомата из начального состояния в любое другое состояние;

— степень различимости r – минимальная длина эксперимента, достаточная для различения любых двух состояний автомата.

Наличие априорной информации в виде оценок d и r позволяет сократить высоту дерева управления до величины h=d+r+ l. Наибольший интерес представляет априорная оценка r. Тогда появляется уникальная возможность восстановления автомата относительно начального дерева высоты (r+ 1) с последующим ростом вершин лишь только из вершин текущего базиса.