
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет переходных процессов методом переменных состояния
|
|
Отметим следующие свойства переменных состояния:
1. В качестве переменных состояния в электрических цепях следует выбирать токи 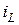 в индуктивностях и напряжения
в индуктивностях и напряжения 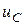 на емкостях.
на емкостях.
2. Дифференциальные уравнения цепи относительно переменных состояния записываются в канонической форме, т.е. представляются решенными относительно первых производных переменных состояния по времени.
3. Число переменных состояния равно порядку системы дифференциальных уравнений исследуемой электрической цепи.
4. Выбор в качестве переменных состояния токов 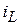 и напряжений
и напряжений 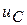 удобен еще и потому, что именно эти величины согласно законам коммутации в момент коммутации не изменяются скачком.
удобен еще и потому, что именно эти величины согласно законам коммутации в момент коммутации не изменяются скачком.
5. Переменные состояния 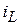 и
и 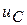 потому так и называются, что в каждый момент времени задают энергетическое состояние электрической цепи, так как последнее определяется суммой выражений
потому так и называются, что в каждый момент времени задают энергетическое состояние электрической цепи, так как последнее определяется суммой выражений 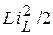 и
и 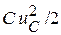 .
.
6. Представление уравнений в канонической форме очень удобно при их решении с помощью персонального компьютера и необходимого пакета прикладных программ. Алгоритм составления этих уравнений для любой электрической цепи следующий. Сначала записывают уравнения по законам Кирхгофа, а затем выбирают переменные состояния и путем дифференцирования исходных уравнений и исключения других переменных получаются уравнения метода переменных состояния. При наличии опыта можно ускорит составление этих уравнений.
В настоящее время широкое распространение получили специальные компьютерные математические системы Eureka, Merkury, MatLAB, Mathematica и другие, среди которых наиболее популярна система MathCAD.
Численные методы анализа переходных процессов основаны на методах приближенного интегрирования систем дифференциальных уравнений. Приближенное интегрирование производится путем разбиения промежутка времени, в пределах которого требуется получить решение, на малые интервалы времени 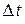 , называемые шагом интегрирования. Интегрирование осуществляется последовательно на каждом интервале и расчет ведется шаг за шагом, начиная с момента
, называемые шагом интегрирования. Интегрирование осуществляется последовательно на каждом интервале и расчет ведется шаг за шагом, начиная с момента 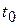 . Существует большое число различных формул численного интегрирования дифференциальных уравнений.
. Существует большое число различных формул численного интегрирования дифференциальных уравнений.
Итак, составим систему уравнений по законам Кирхгофа для схемы предыдущего примера рис. б без индекса 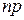 .
.
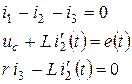 .
.
После преобразований получим систему дифференциальных уравнений в канонической форме:
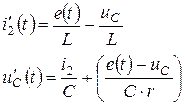
Ниже приводится фрагмент решения с помощью программы Mathcad.
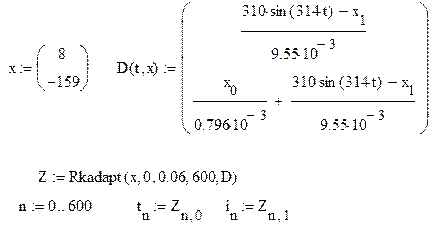 ,
,
где: 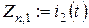 .
.
Ниже приводится график изменения тока 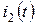 переходного режима
переходного режима
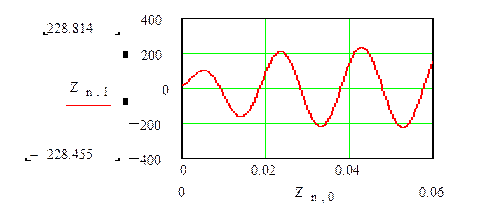
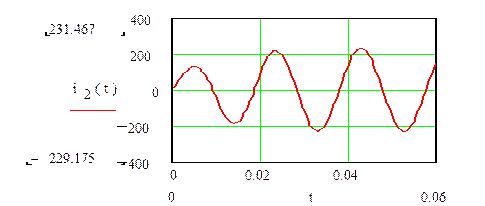
Для сравнения приводится график тока 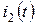 переходного режима, полученного классическим методом
переходного режима, полученного классическим методом
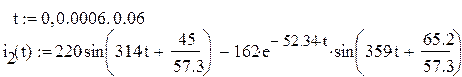
Литература
| № п/п | Библиографическое описание | Тип (учебник, учебное пособие, учебно-методическое пособие, практикум и др.) | Количество в библиотеке |
| Теоретические основы электротехники: [в 3 т.]: учеб. для вузов: Т.1 / К.С. Демирчан [и др.]. – 4-е изд., доп. для самостоят. изучения курса; Гриф МО. – СПб.: Питер, 2006. - 462 с. | Учебник | ||
| Теоретические основы электротехники: [в 3 т.]: учеб. для вузов: Т.2 / К.С. Демирчан [и др.]. – 4-е изд., доп. для самостоят. изучения курса; Гриф МО. – СПб.: Питер, 2006. - 575 с. | Учебник | ||
| Сборник задач по теоретическим основам электротехники: учеб. пособие для вузов / Л.А. Бессонов [и др.]; под ред. Л.А. Бессонова.- 4-е изд., перераб. и испр.; Гриф МО.- М.: Высш. шк., 2003. - 528 с | Учеб.пособие | ||
| Шакурский В.К. Теоретические основы электротехники: учеб.-метод. пособие. Ч.1. Анализ установившихся режимов в линейных электрических цепях / В.К. Шакурский; ТГУ; каф. «Электроснабжение и электротехника». - ТГУ. – Тольятти: ТГУ, 2007. - 77 с. | Учеб.метод. пособие | ||
| Шакурский В.К. Теоретические основы электротехники: учеб.-метод. пособие. Ч.2. Анализ переходных режимов в линейных электрических цепях / В.К. Шакурский; ТГУ; каф. «Электроснабжение и электротехника». - ТГУ. – Тольятти: ТГУ, 2007. - 71 с. | Учеб.метод. пособие | ||
| Шакурский В.К. Теоретические основы электротехники: учеб.-метод. пособие. Ч.2. Аналитические и численные методы анализа динамических режимов в электрических цепях / В.К. Шакурский; ТГУ; каф. «Электроснабжение и электротехника». - ТГУ. – Тольятти: ТГУ, 2007. - 106 с. | Учеб. метод. пособие | ||
| Шакурский В.К. Теоретические основы электротехники: учеб.-метод. пособие. Ч.3. Анализ электромагнитного поля / В.К. Шакурский, В.Н. Кузнецов; ТГУ; каф. «Электроснабжение и электротехника». - ТГУ. – Тольятти: ТГУ, 2008. - 67 с. | Учеб. метод. пособие | ||
| Шакурский В.К. Теоретические основы электротехники. Методы исследования электрических цепей: учеб.-метод. пособие / В.К. Шакурский, М.В. Шакурский. ТГУ; каф. «Электроснабжение и электротехника». - ТГУ. – Тольятти: ТГУ, 2007. - 58 с. | Учеб. метод. пособие | ||
| Шакурский В.К. Теоретические основы электротехники: сб. задач по расчёту нелинейных электрических цепей / В.К. Шакурский, Н.Е. Кузнецов. – Тольятти: ТолПИ, 1991. 113 с. | Учеб. пособие |