II. Объём самостоятельной работы

В течение семестра предусмотрено 37 часа самостоятельной внеаудиторной работы студентов.

III. СОДЕРЖАНИЕ САМОСТОЯТЕНЬНОЙ РАБОТЫ СТУДЕНТОВ

Самостоятельная работа студентов по дисциплине «Автоматизация и управление процессами теплогазоснабжения и вентиляции» должна начинаться с проработки и осознания информации полученной на лекционных занятиях. Результатом такой работы может стать шаг за шагом свободное владение навыками применения конкретных схем автоматизации и построения их математических моделей. При этом задачи построения могут быть сформулированы как преподавателем, так и самим студентом.

Для полного освоения курса студенту необходимо самостоятельно разобраться со следующим перечнем вопросов, которые дадут возможность в полном объеме использовать полученные данные для автоматизации систем ТГВ. В соответствии с рабочей программой на самостоятельное изучение выносятся следующие вопросы:

3.1 Классификация и принципы работы систем регулирования

3.2 Свойства объектов регулирования.

3.3 Качество регулирования

3.4.Автоматические регуляторы. Типовые законы регулирования

По приведенным темам за семестр необходимо написать и доложить пару рефератов и выполнить контрольно-курсовую работу

Выполнение контрольно-курсовой работы:

Содержание ККР:

1. Составить алгоритмическую схему системы автоматического регулирования

2. Составить математическую модель системы: определяются дифференциальные уравнения для каждого звена и определяются передаточные функции основных элементов и их параметры. Определяется передаточная функция замкнутого и разомкнутого контура системы.

2. Описать принцип работы системы.

3. С помощью критериев устойчивости проверить устойчивость линейной части системы при заданных параметрах (критерий Гурвица, Михайлова, Найквиста).

4. Методом D - разбиения построить область устойчивости по одному параметру (по коэффициенту усиления системы) и определить его оптимальное значение.

5. Построить логарифмические частотные характеристики системы.

6. Построить график переходного процесса для исходной системы.

7. Определить корректирующее устройство системы, исходя из заданных значений перерегулирования и времени переходного процесса ()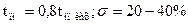

8. Методом трапеций построить график переходного процесса скорректированной системы и оценить его по показателям качества.

9. Используя принципы моделирования, получить все графики в пакете MATHLAB

10. Сделать выводы

Методические указания к выполнению контрольно-курсовой работы:

ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ.

Рассмотрим дифференциальное уравнение движения системы автоматического регулирования, записанного для регулирования величины y(t) при равенстве нулю возмущенных воздействий:

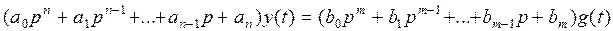
Коэффициенты а₀,..., а_п и b₀,..., b_m представляют собой постоянные величины, а оператор p = d/dt.

Процесс регулирования определяется решением дифференциального уравнения, как сумма двух решений - частного и общего решения:

1

Второе слагаемое характеризует переходную составляющую процесса регулирования.

Система будет называться устойчивой, если с течением времени 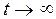переходная составляющая будет стремиться к нулю. Для определения этой составляющей составляется характеристическое уравнение, которое приравнивается к нулю

2

Чтобы определить, устойчива система или нет, нет необходимости решать характеристическое уравнение и определять его корни. Необходимо лишь определить свойства корней, которые достаточны для того, чтобы система была устойчивой. Эти свойства перечислены [1, 2].

Критерий устойчивости Гурвица.

Критерий устойчивости сводится к тому, что при а₀ > 0 должны быть больше нуля все n определителей Гурвица, получаемых из квадратной матрицы коэффициентов. Для характеристического уравнения (2) составляется квадратная матрица коэффициентов, содержащая n строк и n столбцов:

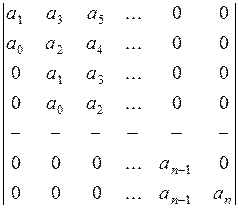3

Частные случаи применения критерия устойчивости Гурвица для систем различных порядков можно найти [2].

Из [2] видно, что уже для уравнения пятого порядка условия устойчивости по критерию Гурвица получаются достаточно громоздкими, поэтому использование этого критерия ограничено уравнением четвертого порядка.

Критерий устойчивости Михайлова.

Критерий устойчивости Михайлова в измененном виде, который будет применяться для определения устойчивости в курсовой работе, можно сформулировать так: для устойчивой системы кривая Михайлова проходит последовательно n квадрантов.

Рассмотрим характеристический полином

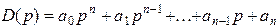4

Подставим в этот полином р = jw. При этом получим характеристический полином

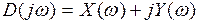5

где:

вещественная часть будет содержать четные степени w:

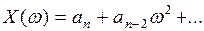6

а мнимая - нечетные степени:

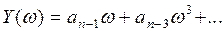7

Составляется таблица для построения кривой Михайлова по точкам, причем задаются различные значения частоты w, по формулам (6) и (7) вычисляются X(w) и Y(w). Затем строится кривая Михайлова и определяется устойчивость системы.

Критерий устойчивости Найквиста.

Чтобы система в замкнутом состоянии была устойчивой, необходимым и достаточным условием является то, что амплитудно-фазовая характеристика этой системы в разомкнутом состоянии не должна охватывать точку с координатами (-1; j0).

Составляется передаточная функция разомкнутой системы:

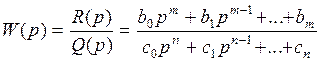8

При подстановки p = jw, получим частотную передаточную функцию разомкнутой системы

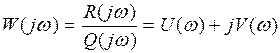9

Затем по формулам определяем модуль и фазу частотной передаточной функции.

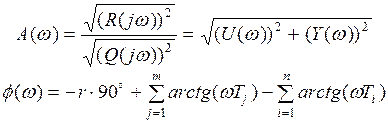10

Задаваясь различными значениями частоты от нуля до бесконечности, можно вычислить модуль и фазу. По модулю и фазе легко строится вектор W= (jw), либо вычисляются предварительно вещественная и мнимая части частотной передаточной функции:

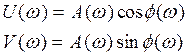11

Результаты расчетов вещественной и мнимой частей частотной передаточной функции при различных частотах сводятся в таблицу, затем строится амплитудно-фазовая характеристика. По этой характеристики определяется устойчивость системы.

ПОСТРОЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ.. D - РАЗБИЕНИЕ.

При расчете и проектировании системы автоматического регулирования иногда бывает необходимо исследовать влияние ее различных параметров на устойчивость. Для решения этой задачи определяются области значений параметров, при которых система оказывается устойчивой.

D - разбиение в плоскости двух параметров.

Составляется характеристическое уравнение (.2), заменяется оператор р = jw, составляя тем самым характеристический комплекс (4). Раскладывая характеристический комплекс на действительную и мнимую части, определяется граница устойчивости (5) и (6). Приравнивая эти уравнения к нулю и решаются они совместно относительно каких-либо двух параметров системы.

Задаваясь затем различными значениями частоты в пределах от нуля до бесконечности по полученным формулам из совместного решения (5), (6) вычисляются значения искомых параметров, которые заносятся в таблицу. По полученным данным строится кривая D - разбиения на плоскости этих двух параметров.

Для упрощения выделения границ области устойчивости из всего комплекса кривых D - разбиения на плоскости двух параметров вводится штриховка этих кривых по правилу: перемещаясь вдоль кривой в сторону увеличения частоты, надо штриховать ее с левой стороны, если будет положителен определитель, составленный из частных производных. Если же определитель отрицателен, то кривую надо штриховать справа.

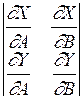12

При соблюдение этого правила штриховка будет направлена внутрь области устойчивости.

СИНТЕЗ СИСТЕМЫ С ПОСЛЕДОВАТЕЛЬНОЙ КОРРЕКЦИЕЙ С ПОМОЩЬЮ ЛАЧХ.

Построение ЛАЧХ и ФЧХ

Амплитудная и фазовая частотные характеристики получаются из амплитудно-фазовой характеристики (АФХ)

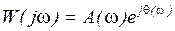131

где A(w) - амплитудно - частотная характеристика (АЧХ);

q(w) - фазочастотная характеристика (ФЧХ).

Логарифмические амплитудные и фазовые частотные характеристики получаются при логарифмировании АФХ

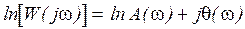14

При построении логарифмической амплитудной характеристики пользуются не натуральными, а десятичными логарифмами. Под логарифмической амплитудно-частотной характеристикой (ЛАЧХ) понимается зависимость

15

Под фазовой характеристикой понимают (ФЧХ)

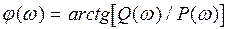16

При построении этих характеристик используется стандартная сетка. По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие lg w, а отметок пишется само значение частоты в рад/сек. Нулевой отметки частоты нет, т.к. lg0 не существует, поэтому вертикальная ось проводится через любую точку на горизонтальной оси. По оси ординат откладывают две величины: логарифм модуля и фазы.

Главным достоинством логарифмических амплитудных частотных характеристик является возможность построения их во многих случаях практически без вычислительной работы. Это особенно проявляется в тех случаях, когда частотная передаточная функция может быть представлена в виде произведения сомножителей. Тогда суммирующая ЛАХ может быть найдена суммированием ординат, соответствующих отдельным сомножителям. Часто не требуется даже такого суммирования и результирующая может быть приближенно построена в виде так называемой асимптотической ЛАЧХ, представляющая собой совокупность отрезков прямых линий с наклонами, кратными величине 20 дб/дек. Логарифмические характеристики последовательного соединения звеньев строят непосредственно по передаточным функциям без построения характеристик отдельных звеньев.

1. Через точку w = 1 проводят прямую с наклоном 20lg K.

2. Через точки w_i=1/T_i проводят вертикальные линии, каждой постоянной времени будет соответствовать своя линия.

3. Строят участки логарифмической амплитудной характеристики между частотами сопряжений w_i, начиная с крайне левой частоты сопряжения. На каждой частоте сопряжения логарифмическая характеристика меняет свой наклон. Если соответствующая постоянная времени находится в числителе, то наклон изменяется на +20 или +40 dB на декаду в зависимости от порядка соответствующего множителя. Если же постоянная времени находится в знаменателе, то наклон изменяется на

-20 или - 40 dB на декаду в зависимости от порядка соответствующего множителя.

4. Фазовую характеристику строят по точкам.

Выбор последовательной коррекции с помощью ЛАЧХ.

Коррекцию осуществляют для повышения запаса устойчивости путем введения дополнительных звеньев. Коррекцию можно вводить тремя разными, но основными способами. Последовательная коррекция - это один из этих способов.

Алгоритм проведения коррекции:

1. построение ЛАЧХ и ФЧХ нескорректированной разомкнутой системы.

2. Построение ЛАЧХ скорректированной (желаемой) системы. Эта ЛАЧХ состоит из трех асимптот - низкочастотной НЧА, среднечастотной СЧА и высокочастотной ВЧА и двух участков, сопрягающих среднечастотную асимптоту с низко- и высокочастотными. Порядок построения желаемой ЛАЧХ принимается следующий:

а. определяется частота среза w_ср, модули L₁=/L₂/ и угол m как запасы устойчивости по амплитуде и фазе. В основу синтеза положены следующие показатели качества: перерегулирование при ступенчатом воздействии на входе и время переходного процесса. Зная их по кривым номограмм [1, 2, 3] определяем P_max, P_min, w_п, w_ср.

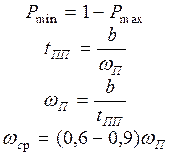17

Зная значения P_max, P_min по номограмме [1, 2, 3] определяем запасы устойчивости по модулю и фазе.

б. строится среднечастотная асимптота. Учитывая, что СЧА определяет качество переходного процесса системы и запас устойчивости по амплитуде и фазе. проходит СЧА через частоту среза с наклоном 20dB/дек, что обеспечивает достаточный запас устойчивости по фазе в промежутке по оси ординат от L₁ до L₂, что дает достаточный запас устойчивости по модулю (рис 7.1).

в. строятся низко- и высокочастотные асимптоты так, чтобы они в возможно большем диапазоне частот совпадали с ЛАЧХ нескорректированной системы. Это упрощает схемы корректирующих устройств и их выбор.

г. СЧА сопрягается с НЧА и ВЧА. Сопряжение производится прямыми с наклонами -20, -40, -60 dB/дек. Желательно, чтобы этот наклон отличался от наклона ЛАЧХ нескорректированной системы в том же диапазоне частот не более чем на 20dB/дек. Желательно также, чтобы сопряжение производилось в точках сопряжения участков ЛАЧХ нескорректированной системы. Все это ведет к простым корректирующим звеньям, что является основным признаком при выборе НЧА, ВЧА и отрезков, сопрягающих их с СЧА.

3. Построение ЛАЧХ последовательного корректирующего устройства производится в соответствии уравнения

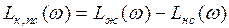18

Логарифмические амплитудно-частотные

характеристики системы с последовательной

коррекцией.

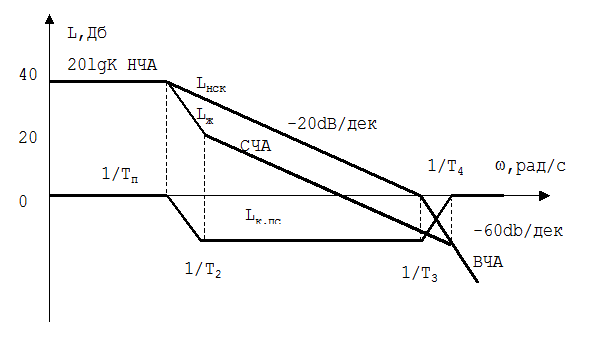
Рис.1

По построенной ЛАЧХ определяются звенья, из которых она может быть получена, и их параметры. Практически это делается по справочным таблицам [1, 2, 3], где приведены ЛАЧХ типовых корректирующих устройств, и их принципиальные электрические схемы и зависимости, позволяющие определить параметры.

4. если при выполнении последовательного корректирующего устройства возникают трудности, то оно может быть заменено параллельным устройством. Это делается на основании их одинаковых действий и, следовательно, на основании их равенства их передаточных функций.

ПОСТРОЕНИЕ ПЕРЕХОДНОГО ПРОЦЕССА.

Существует много методов построения переходных процессов. Из линейных методов получили распространение классический, операторный и частотный. В курсовой работе для анализа используется частотный метод. Он не требует определение корней характеристического уравнения, но и имеет пониженную точность расчета, связанную с погрешностью графических построений и аппроксимации кривой прямолинейными отрезками.

Построение переходного процесса производится по действительной или мнимой части частотной характеристики замкнутой системы

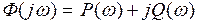8.1

Наибольшее распространение получил метод расчета действительной части частотной характеристики замкнутой системы.

Алгоритм построения переходного процесса:

1. Строится график P(w).

2. Производится замена мало отличающих от кривой горизонтальными и наклонными прямолинейными участками, образующие с осью с осью ординат трапеции (рис 8.1). Каждая трапеция характеризуется параметрами (рис.8.2):

а. высотой Р

б. полной полосой пропускания частоты w₀

в. полосой равномерного пропускания частот w_d

г. коэффициент наклона x =w_d/w₀

3. По таблице в [1, 2, 3] для каждого коэффициента наклона определяется функция времени 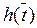, и все заносится в таблицу.

4. Так как таблицы созданы для единичных трапеций производится пересчет масштабов, потому что реальные трапеции отличаются от единичной:

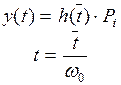19

Все данные записываются в таблицу.

Аппроксимация кривой

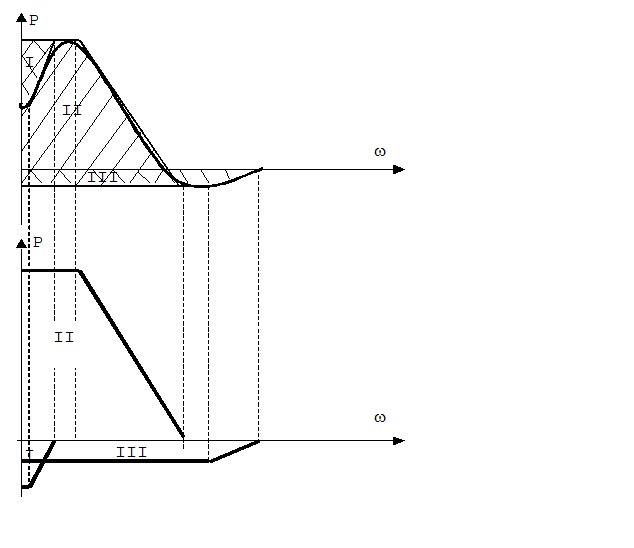Рис. 2

Параметры трапеции

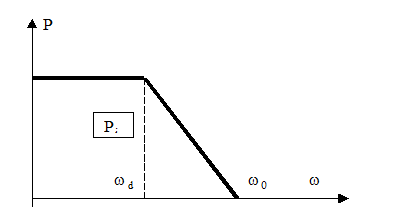
Рис 3

5. По данным из таблицы строится переходные процессы для каждой из трапеций.

6. Производится алгебраическое суммирование ординат при определенных t, а это дает расчетную кривую переходного процесса системы рис. 8.3.

7. По графику определяется значения перерегулирования s и время переходного процесса t_П рис.8.4.

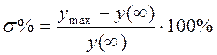
В большинстве случаев считается, что если величина перерегулирования не будет превышать 10-30%, то запас устойчивости будет достаточным.

Графики переходного процесса

Рис.4

Определение s и t_П

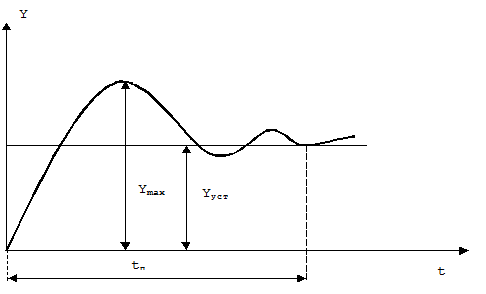
Рис.5

Следует отметить, что самостоятельная работа студента не должна сводиться только к изучению лекционного материала, но и поиск дополнительной информации в различных источниках с целью расширения знаний. При этом самое трудное – найти нужную и полезную информацию в большом перечне рекомендуемой литературы. И здесь не обойтись без помощи и совета преподавателя.

При этом формой отчетности или проверки выполнения выносимых на самостоятельное изучение вопросов является диалог преподавателя со студентом. В некоторых случаях формой отчетности является реферат с раскрытием одного или нескольких разделов выносимых на самостоятельное изучение.

Большая часть самостоятельной работы студента связана с выполнением индивидуального задания (контрольно-курсовой работы). При этом необходимо отметить, что ритм имеет огромное значение в организации самостоятельной работе студентов над индивидуальным заданием. Ритмичная работа студентов во много раз производительнее, чем так называемые авралы, когда в короткое время с неренапряжением сил выполняются работы, рассчитанные на длительный период. Один из способов оптимизации самостоятельной работы необходимо внедрение поэтапного графика выполнения самостоятельной работы. При этом студенту необходимо установить (самостоятельно или с помощью преподавателя) оптимальное число и сроки контрольных пунктов (вопросов), тщательно спланировать объем работы, намеченных для выполнения к этим пунктам, предусмотреть эффективные способы выполнения каждого этапа.

Необходимо исключать непродуктивные затраты времени на формальные, трудоемкие, многократно повторяющиеся, но мало что дающие работы.

Студент должен осознавать, что выполнение самостоятельной работы неизбежно потребует его обращение к преподавателю за помощью и советами. При этом помощь может оказывается или опосредованно – через опубликованные методические рекомендации, или непосредственно – во время консультаций. Поэтому посещение консультаций должно является неотъемлемой частью самостоятельной работой студентов. Консультация - это совместный анализ, обсуждение работы, диалог студента и преподавателя, который научит студента точно выражать свои мысли, активно отстаивать свою точку зрения, аргументированно возражать, опровергать ошибочную позицию. Кроме того:

- сориентировать студента в источниках информации;

- выявить наличие пробелов в знаниях и умениях и дать рекомендации по ликвидации тех пробелов, без которых студент не сможет выполнить работу;

- выявить недостатки в организации работы, которые снижают темп и эффективность выполнения работы;

- познакомить со способами самоконтроля, самоанализа промежуточных и конечных результатов.

Конечным результатом выполнения индивидуального задания является оформленная в соответствии с установленными требованиями контрольно-курсовая работа и написанный на темы выделенные для самостоятельного изучения реферат. При этом успешно выполненной контрольно-курсовой работой и рефератом считается та или тот, которые прошли публичную защиту. Защита контрольно-курсовой работы заключается в ответе студентом на несколько вопросов по теме работы, а защита реферата в публичном докладе по теме реферата.