Их образами в языке и мышлении

Умозаключения как форма мышления

Предметы, явления действительности находятся во взаимо­действии. Отображением предметов в наших мыслях служат по­нятия об этих предметах и суждения, которые формируются с помощью понятий. Поэтому суждения о понятиях, как и их об­разы в реальном мире, тоже находятся во взаимодействии. Взяв за основу истинные исходные суждения (посылки), мы делаем выводы (умозаключения) о тех понятиях, которые фигурирова­ли в суждениях. Связь между ними наглядно можно представить в виде схемы (рис. 5.6).

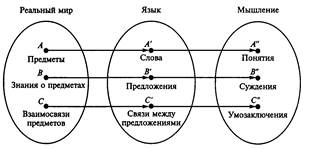
Иллюстрация связи между объектами реального мира,

их образами в языке и мышлении

Существует соответствие между объектами действительности, их образами в языке и в мышлении.

Но не всякое сочетание суждений дает умозаключение. Для того чтобы из одного или нескольких исходных суждений (посылок) получились умозаключения, надо знать правила и законы, по ко­торым они образуются.

Приведем три правила образования умозаключений.

Необходимо, чтобы исходные суждения были истинными.

Формирование умозаключений можно проводить только по строго определенным законам, которые необходимо изучить.

Нарушение этих правил ведет к ложным умозаключениям.

Умозаключение — это форма мышления, посредством которой из одного или нескольких суждений на основании правил выво­дится новое суждение. В состав умозаключения входят посылки, вывод и заключение.

Посылки — это исходные суждения.

Заключение есть новое суждение, полученное из посылки ло­гическим путем.

Вывод — логический переход от посылки к умозаключению.

Окружающий мир имеет многообразные формы связи между своими объектами, поэтому и в мышлении существуют различ­ные виды умозаключений.

По направлениям логического следования умозаключения де­лятся на: дедуктивные — от общих суждений к частным, индук­тивные — от частных суждений к общим, по аналогии — от част­ных суждений к частным.

По степени достоверности умозаключения бывают: достовер­ными (истинными, демонстративными) и вероятностными (прав­доподобными, недемонстративными).

Умозаключения являются логическими Моделями рассуждений. В зависимости от характера умозаключений выводы при истинных посылках и заключениях могут получаться как достоверные, кото­рые обязательно будут иметь место, так и вероятностные, кото­рые могут произойти лишь с определенной долей вероятности.

Дедуктивные умозаключения также можно классифицировать в зависимости от количества истинных посылок:

Непосредственные,

опосредованные, например

Так, дедуктивное опосредованное умозаключение может иметь вид:

Всякий порок заслуживает наказания

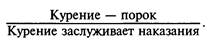
Здесь и далее над чертой будем писать посылки, под чертой — заключение.

Для того чтобы заключения были истинными, необходимо знать способы их получения, т.е. логическую связь между посылками и заключением. Незнание законов логики ведет к ложным заключе­ниям. Например, оцените истинность заключений:

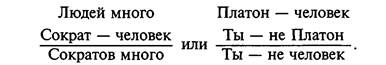
Здесь нет игры слов, просто неправильно построен вывод. Дру­гой пример неправильного построения вывода:

Все математики изучали математическую логику

Правильное заключение имеет вид: «Некоторые, кто имеет выс­шее образование, изучали математическую логику».

Правильные дедуктивные умозаключения образуются через отношение логического следования между посылкой и заключе­нием. Истинные посылки, если соблюдены все необходимые пра­вила выводов (т.е. импликация истинна), всегда приводят к ис­тинному заключению.

Поэтому дедуктивные умозаключения — самый строгий вид умозаключений, который при соблюдении всех правил всегда дает достоверный результат. Дедуктивные рассуждения являются основным видом рассуждений, применяемых в математике. «Выс­шим долгом физиков является поиск таких элементарных зако­нов, из которых путем чистой дедукции можно получить карти­ну мира», — писал Альберт Эйнштейн о физике, которая для доказательств законов природы использует математический язык.