
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мартовский и сентябрьский календарные стили. Перевод древнерусских дат на современное летосчисление.
|
|
Система летосчисления определяется эрой и стилем, т.е. началом года. В Древней Руси была принята византийская система от сотворения мира, просуществовавшая до 1700 г. Год начинался в марте или сентябре. Приняв эру от Византии, Русь сохранила исконное славянское весеннее начало года. Смена мартовского стиля сентябрьским произошла в конце XV в.
Одной из важнейших задач хронологии как вспомогательной исторической дисциплины является разработка принципов согласования различных систем датировок и перевода (редукции) дат с одной системы на другую.
При переводе указанных в источниках дат от сотворения мира необходимо учитывать следующие обстоятельства. Прежде всего, надо установить истинную дату, так как при указании на нее источника могли быть опущены цифры, обозначающие тысячелетие и столетие. Известно, что, например, в XV в. часто указывались только две последние цифры даты - «в лето 77», а в XVII в. опускались цифры, обозначавшие тысячелетие, — «в лето 150». Подобными сокращениями при указании на даты часто пользуются и сейчас, например: «Отечественная война 12-го года» и т. д.
Установив полную дату от сотворения мира, следует вычесть из нее 5508, так как по византийской эре сотворение мира произошло за 5508 лет до Рождества Христова. Однако установленный таким способом год от Рождества Христова будет точной датой только при определенных условиях. Дело в том, что при вычитании числа 5508 не учитывается одно очень важное обстоятельство, а именно начало указанного в источнике года.
Существование сентябрьского и мартовского стилей усложняет перевод дат с византийской системы на современную. К тому же мартовский стиль на Руси имел еще две разновидности - ультрамартовский и цирка-мартовский годы.
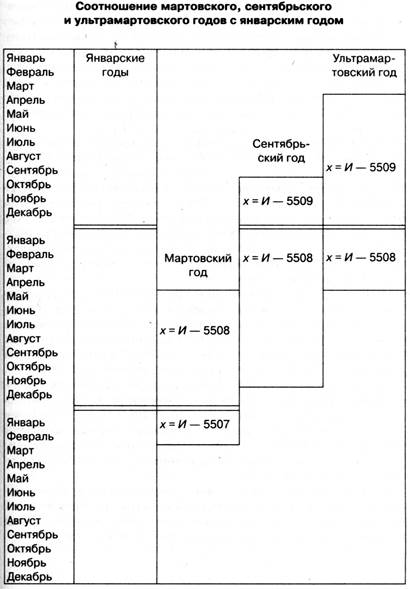
В распоряжении историков имеются специальные таблицы, отражающие соотношение сентябрьского, мартовского и ультрамартовского годов с современным январским. Тем не менее, историку необходимо уяснить сущность соотношений стилей и правила перевода дат на современную систему времясчисления.
Проследим эти правила на конкретном примере. Предположим, что в источнике указана дата - 30 апреля 6510 г. Если этот год начинался в марте, то, следовательно, он запаздывал в сравнении с январским на два месяца (январь, февраль), а остальные десять месяцев (с марта по декабрь) у них совпадали. Таким образом, для дат в пределах совпадающих месяцев при определении искомого январского года (X) из указанной даты от сотворения мира следует вычитать 5508. В нашем примере Х= 6510—5508 = 30 апреля 1002 г. Если в источнике указана дата в пределах января и февраля, например 30 января, то расчет несколько изменится. В этом случае январь и февраль, заканчивавшие мартовский 6510 г., относились уже к следующему (Х+1) январскому году. В этом случае Х = (6510— 5508) + + 1 = 30 января 1003 г. Отсюда следует, что для правильного определения даты, приходящейся на январь и февраль в мартовском году, из нее следует вычитать не 5508, а на единицу меньше — 5507.
Возьмем другой пример. В источнике указана дата 30 апреля 7150 г Известно, что этот год начинался в сентябре. По отношению к нему январский год отставал на четыре месяца — сентябрь, октябрь, ноябрь и декабрь. Совпадали же у них восемь месяцев — с января и август. Так как указанная в примере дата приходится на один из сов падающих месяцев, здесь действует общее правило, т.е. из 7150 нужно вычесть 5508 и искомая дата, таким образом, будет 30 апреля 1642 г. Но если какое-либо событие произошло, например, 30 октября этого же 7150 сентябрьского года, то оно приходится на еще не завершившийся предыдущий январский год (X — 1). Следовательно, в этом случае Х = (7150 — 5508) — 1 = 30 октября 1641 г.
Таким образом, для определения даты, приходящейся на период сентября по декабрь включительно, в сентябрьском году из нее следует вычитать не 5508, а на единицу больше — 5509. В Древней Руси существовал еще так называемый ультрамартовский (от латинского слова «ультра» — по ту сторону) стиль, употреблявшийся в XII—XIV вв. параллельно с мартовским. В отличие от последнего, ультрамартовский год не запаздывал на два месяца по отношению к январскому году, а опережал его, начинаясь на десять месяцев раньше. В этом отношении он подобен сентябрьскому году. Общими в январском и ультрамартовском годах были январь и февраль. Следовательно, если какое-то событие произошло в пределах этих двух месяцев, для перевода даты надо вычитать 5508. Поскольку первые десять месяцев (с марта по декабрь) ультрамартовского года приходились еще на предыдущий январский (Х—1) год. Для определения даты события, происшедшего с марта по декабрь включительно, надо вычитать из нее на единицу больше — 5509. Нетрудно заметить, что ультрамартовский стиль исходит из того, что от сотворения мира до Рождества Христова прошло не 5508, а 5509 лет.
Новогодие на Руси не было твердо установленным числом и могло приходиться как на начало марта, так и на конец февраля, приурочиваясь к первому весеннему полнолунию. Такие годы называются цирка-мартовскими или цирка-ультрамартовскими (от латинского слова «цирка» — вокруг). Правила перевода дат для этих годов остаются те же самые, что для мартовского и ультрамартовского стилей. Нужно только учитывать, что вычитать необходимое число следует с января до того дня, когда начался новый год, или со дня нового года по декабрь включительно.
Предположим, что в 6610 г. мартовский год начался 11 марта. С январским годом совпадают, как мы уже выяснили раньше, десять месяцев (с марта по декабрь). В данном же случае совпадают не все числа марта, а только с 11 по 31. Следовательно, вычитать 5508 нужно только при переводе дат, приходящихся на период с 11 марта по 31 декабря, а с января по 10 марта следует вычитать 5507. Соответственно определяются даты, указанные по ультрамартовскому стилю, но с поправкой на один год.
Если в источнике нет указания на месяц событий, то установить его абсолютную точную дату по январскому календарю невозможно.
При переводе дат всегда следует помнить, что они определяются по Юлианскому календарю, или по старому стилю. Чтобы выразить; установленную дату по новому стилю, надо ввести соответствующую поправку, т.е. увеличить ее на необходимую разницу между старым и новым стилями. Эта поправка необходима для датировки событий, происшедших после введения в 1582 г. Григорианского календаря.
Индикты. Индиктом называется число, обозначающее порядковое место года в текущем 15-летнем цикле. Счет времени индиктами на Руси был заимствован у Византии. По-видимому, такой счет сложился в римском Египте на основе периодического пересмотра налоговых списков (вероятно, сам термин происходит от латинского слова «индикцион» — объявление, провозглашение, или «индико» — объявляю, назначаю). В Древнем Риме при императоре Диоклетиане каждые 15 лет в империи проводилась переоценка имущества для правильного налогообложения. Введение индиктового счета времени в Византии связывают с императором Константином, который ввел новое счисление с 23 сентября 312 г. Число месяца было избрано не случайно — это был день рождения первого римского императора Октавиана Августа. В 462 г. из практических соображений начало отсчета индиктов было перенесено на 1 сентября. Исходной точкой отсчета индиктов являлось сотворение мира. В 537 г. император Юстиниан ввел датировку по индиктам как обязательную. В Священной Римской империи она употреблялась вплоть до ее распада в 1806 г.
Индикт года определяется делением даты от сотворения мира на 15 по сентябрьскому календарному стилю. Остаток от деления показывает индикт. Например, требуется установить индикт 6777 г. от сотворения мира. 6777: 15 = 451 и 12 в остатке, следовательно, от сотворения мира прошли 451 полных 15-летних цикла, а 12 — это порядковый номер года в текущем 452-м цикле, т.е. индикт 6777 г. Если дата делится на 15 без остатка, то индикт равен делителю, т.е. 15. Следует учитывать, что один индикт имели лишь сентябрьские годы, а январские, мартовские и ультрамартовские имели два индикта. Существуют специальные таблицы для определения дат по индиктам. В письменных источниках индикт или заменяет дату, или дополняет ее. В последнем случае открывается возможность проверки правильности указания источника на дату. Например, в Благословенной грамоте ростовского архиепископа Ефрема старцу Кассиану 1448 г. указано: «А писана грамота на Москве месяца апреля в 11 день в лето 6956 индикта 11». Обычным путем датируем грамоту 1448 г. и проверяем ее. 6956: 15 = 464 и 11 в остатке. Индикт, указанный в грамоте, соответствует дате 6956 от сотворения мира. Если в источнике указан только лишь индикт, но по другим косвенным признакам устанавливаются определенные хронологические рамки источника, например время княжения какого-либо князя, то установление даты по индикту резко сужает круг возможных датировок.
Круги солнца. В Древней Руси существовал счет времени 28-летними циклами солнца. Его исходной точкой, как и при счете индиктами, было сотворение мира. Так как любой календарный год (простой и високосный) не содержат целого числа недель, одни и те же числа ежегодно приходятся на разные дни недели. Такое перемещение чисел имеет определенные закономерности. Простой год содержит 52 недели и 1 день, високосный — 52 недели и 2 дня. Простой год начинается и заканчивается одним и тем же днем недели: если 1 января простого года приходилось на среду, то 31 декабря будет среда. В високосном году, естественно, 31 декабря в данном случае пришлось бы на четверг, 1 января 1979 г. — понедельник, значит, 1 января 1980 г. придется на вторник, но в 1981 г. не на среду, а на четверг, так как 1980 г. високосный, в 1982 г. — на пятницу, в 1983 г. — на субботу, в 1984 г. – на воскресенье, но в 1985 г. не на понедельник (как в 1979 г.), а на вторник, так как 1984 г. високосный. Продолжая дальше эти расчеты, мы легко убедимся, что строгий порядок перемещения чисел по дням недели будет повторяться через каждые 28 лет. Этот 28-летний период называется циклом солнца, а порядковое место года в его пределах — кругом солнца данного года.
Круг солнца определяется аналогично индикту — делением даты от сотворения мира на 28. Остаток от деления показывает круг солнца данного года. К началу нашей эры прошло 196 полных циклов солнца (5508: 28 = 196 и 20 в остатке). Круг солнца 5508 г. равен 20. Следовательно, чтобы облегчить расчет круга солнца для даты от Рождества Христова, к ней надо прибавить 20 и сумму разделить на 28. Например, круг солнца 1980 г. равен 12 - (1980 + 20): 28 = 71 и 12 в остатке.
Указания источников на круги солнца помогают в определении дня недели, а в ряде случаев имеют большое самостоятельное значение для проверки дат.
Вруцелето. Вруцелето — это название воскресного дня в данном году, обозначенное одной из первых семи букв русского алфавита. С помощью вруцелета можно определить день недели для любого числа месяца.
В церковных календарях исходили из предположения, что 1 марта 1 г. от сотворения мира приходилось на пятницу, и ближайшее воскресенье — 3 марта обозначили первой буквой русского алфавита А. Последующие дни недели были обозначены другими шестью следующими буквами, но в обратном алфавиту порядке: понедельник — 3, вторник — S, среда — Е, четверг — Д, пятница — Г, суббота — В. Здесь пропущены буквы Б (буки) и Ж (живете), так как они в Древней Руси не имели цифрового значения.
Итак, Вруцелето данного года — это буква, на которую приходится воскресенье. Каждый год Вруцелето изменяется, переходя на следующую букву (в високосном году через букву). Установленный выше порядок перемещения чисел месяца по дням недели (круги солнца), безусловно, приложим и к смене вруцелет, поэтому определенному кругу солнца соответствует свое Вруцелето. Это соответствие легко устанавливается с помощью специальных таблиц.
Определение дней недели по формулам. В источниках часто имеются указания на день, когда произошло то или иное событие. Это дает дополнительную возможность для проверки указанной в источнике даты. Существует несколько математических формул для определения дня недели.
Формула выдающегося русского астронома академика Д.М.Перевощикова:
Х равен остатку от деления выражения [(Н — 1)-+1/4(Н-1)+(Г-1)]: 7, где
Х — порядковый номер дня недели, считая с воскресенья (воскресенье — 1, понедельник — 2 и т. д., суббота — 0);
Н — число года по эре от Рождества Христова;
Г— число дней от начала года по искомый день включительно.
Пример. Революция 1905 г. началась 9 января в воскресенье. Подставив в формулу соответствующие цифровые данные, мы должны получить Х= 1. Проверим это: Х= [(1905-1) + (9 - 1)]: 7 = [1904 + 476 + 8]: 7 = 2388: 7 = 341 и 1 в остатке.
Формула слависта и филолога академика Е.Ф.Карского: Х равен остатку отделения выражения [Н + 1/4(Н— 1)+(Т+ 5)]: 7.
Значения Х и букв в этой формуле такие же, как и в предыдущей.
Определим значение Х по этой формуле для той же даты 9 января 1905 г. Х= [1905 + 1/4 (1905 - 1) + (9 + 5)]: 7 = 2395: 7 = 342 и 1 в остатке.
Формула Н.И.Черухина: Х равен остатку от деления выражения [(5хН): 4+М+Г]: 7, где
Х — порядковый номер дня недели, считая с понедельника (понедельник — 1, вторник — 2 и т. д., воскресенье — 0);
Н — число данного года по эре от Рождества Христова;
М — цифра данного месяца (эти цифры для простого года начиная с января, следующие — 4, 0, 0, 3, 5, 1, 3, 6, 2, 2, 4, 0, 2; для високосного года, начиная с января, — 3, 6, 0, 3, 5, 1, 3, 6, 2, 4, 0, 2);
Г— указанное число месяца.
Проверим эту формулу на том же примере. По этой формуле остатка от деления быть не должно. Х = [(5 х 1905): 4 + 4 + 9]: 7 = [(9525: 4) + 13]: 7 = (2381 + 13): 7 = 2394: 7 = 342. Остатка нет.
Все эти формулы позволяют определить день недели только по современной эре и для январского года Юлианского календаря (по старому стилю).
Известный историк Н.Г.Бережков вывел универсальную формулу для определения дня недели по эре от сотворения мира и по эре от Рождества Христова как для январского, так и для сентябрьского, мартовского и ультрамартовского годов. По этой формуле Х равен остатку от деления следующего выражения: Х = [Н + 1/4(Н — Р)+ Т+r]: 7, где
Х — порядковый номер искомого дня недели, считая с воскресенья (воскресенье — 1, понедельник — 2 и т. д., суббота — 0);
Н — цифровое обозначение года;
Т— число дней от начала года по искомый день включительно;
Р — 0 в мартовском году, 1 — в январском, сентябрьском и ультрамартовских годах;
г — 3 в ультрамартовском году, 4 — в мартовском, 5 — в сентябрьском и январском годах.
По этой формуле в нашем примере (9 января 1905 г.) остаток должен быть равен 1. Подставим в эту формулу соответствующие цифровые значения: Х= [1905 + 1/4(1905 - 1) + 9 + 5]: 7 = (1905 + 476 + + 9 + 5): 7 = 2395: 7 = 342 и 1 в остатке.
По формулам Д.М.Перевощикова, Е.Ф.Карского и Н.Г.Бережко-ва можно определить день недели и по Григорианскому календарю, но значения Х в этом случае будут другие: понедельник — 1, вторник — 2 и т. д., воскресенье — 0.
Установление дат по праздникам церковного календаря. В исторических источниках нередко вместо точной даты имеются указания на церковный праздник, приходящийся на событие, о котором идет речь. Русские церковные праздники можно разделить на две группы: подвижные (переходящие) и неподвижные (непереходящие). Подвижные праздники не имеют постоянной фиксированной даты и приходятся из года в год на разные числа календаря. Неподвижные праздники отмечаются в одни и те же числа месяца. Из последних в источниках часто можно встретить следующие: Крещение — 6 января, Сретение — 2 февраля, Благовещение Пресвятой Богородицы — 25 марта, Юрьев день весенний — 23 апреля, Николин день весенний — 9 мая, Ильин день — 20 июля, Преображение Господне — 6 августа, Успение Пресвятой Богородицы (Госпожин день) — 15 августа, Семенов день «летоначатца», или «летопроводца», — 1 сентября, Рождество Пресвятой Богородицы — 8 сентября, Введение во храм Пресвятой Богородицы - 21 ноября, Юрьев день осенний — 26 ноября, Николин день осенний — 6 декабря, Рождество Христово — 25 декабря и др. Все даты здесь приведены по Юлианскому календарю.
Встречаются в источниках и указания на определенные посты («говейно», «говение»), например Успенский пост (с 1 по 15 августа), Филиппов, или Рождественский, пост (с 15 ноября по 25 декабря). Что касается подвижных праздников, то все они зависят от Пасхи, отделяясь от нее определенными постоянными сроками (до Пасхи или после нее). Например, Вознесение Господне — четверг, через 39 дней после Пасхи, Вербное воскресенье — за 7 дней до Пасхи, Фомино воскресенье — через 7 дней после Пасхи, вход Господен в Иерусалим — за 7 дней до Пасхи.
Подвижность самой Пасхи объясняется тем, что она рассчитывается по лунному календарю. Все вопросы, связанные с ее определением, называются Пасхалией. Пасха должна праздноваться в первое воскресенье после первого весеннего полнолуния, каким счита ется полнолуние в пределах от 21 марта до 18 апреля. Соответственно первые воскресенья после полнолуния могут приходиться на период от 22 марта до 25 апреля по старому стилю, который получил название «Пасхального предела».
Для определения дня Пасхи пользуются специальными таблицами «обращения великого индиктиона». Великим индиктионом называется порядковый номер года в пределах 532-летнего периода. Передвижение дня Пасхи по числам календаря в определенном порядке повторяется каждые 532 года, так как 28 (солнечный цикл) при умножении на 19 (лунный, Метонов цикл) дает 532. Счет ведется от сотворения мира. Календарный стиль при вычислении дня Пасхи никакой роли не играет, так как она бывает только в марте или апреле, т.е. при установлении соответствия даты январскому году от Рождества Христова в любом случае из даты от сотворения мира следует вычитать 5508.
Для определения дня Пасхи используют формулу немецкого математика К.-Ф.Гаусса. Она была выведена им на рубеже XVIII и XIX вв. для определения Пасхи по Григорианскому календарю, так как католическая западная церковь именно по нему празднует Пасху. Но с определенными поправками она пригодна и для определения дня православной Пасхи. Доказана эта формула была только в 1870 г. другим немецким ученым, профессором Базельского университета Германом Кинкелином.
Для определения Пасхи по этой формуле необходимо найти значение нескольких величин, обозначаемых латинскими буквами a, b, с, d, e:
а равно остатку от деления цифрового обозначения данного года на 19;
b равно остатку от деления той же цифры на 4;
с равно остатку от деления той же цифры на 7;
d равно остатку от деления выражения (19a + 15) на 30;
е равно остатку от деления выражения (2b + 4с + 6d + 6) на 7.
В случае, когда (d + е) будет меньше 9, Пасха придется на март, больше 9 — на апрель. В первом случае, прибавив к сумме (d + е) 22, получим искомую дату. 22 прибавляется и тогда, когда (d+ е) равно 0. Во втором случае искомую дату получим, вычитая из суммы (d+е) цифру 9.
Формула Гаусса рассчитана для определения дня Пасхи по датам эры от Рождества Христова.
Метонов (лунный) цикл. Фазы Луны приходятся на одни и те же дни солнечного календаря через каждые 19 лет. Этот цикл бы.1 установлен греческим астрономом Метоном в V в. до н.э. и назван его именем.
Порядковый номер года внутри незавершенного 19-летнего цикла называется «золотым числом» или кругом Луны. Название «золотое число» объясняется тем, что в Древнем Риме оно писалось золотыми буквами на специальных досках, выставлявшихся для сведения граждан. Для определения «золотого числа» необходимо к дате от Рождества Христова прибавить единицу и полученную сумму разделить на 19. Остаток покажет искомое число. Прибавление к дате единицы определяется тем, что 1 г. от Рождества Христова считался вторым в лунном цикле.
В византийской и древнерусской хронологии это число называлось «кругом луны» и вычислялось несколько по-иному. Так как от сотворения мира до Рождества Христова считалось 5508 лет, 1 в. до н. э. оказывался 17-м в незавершенном 19-летнем цикле (5508: 19 = 289 и 17 в остатке). Следовательно, круг луны 1 г. н. э. = 18; 2 г. н. э. = 19; 3 г. н. э. = 1 и т. д. По эре от Рождества Христова считалось, что золотое число 1 г. н. э. = 2, значит, для 2 г. н. э. оно равно 3, для 3 г. н. э. — 4 и т. д. Таким образом, разница между «золотым числом» и кругом луны всегда сохраняется равной трем и, чтобы определить круг луны для даты от Рождества Христова, из нее необходимо вычесть две единицы и разность разделить на 19; остаток покажет круг луны. (Одна единица прибавляется к дате при определении «золотого числа», а три единицы вычитаются из нее при определении круга луны, поэтому удобнее сразу же вычитать две единицы.)
Например, круг луны 1649 г. равен 13, так как (1649 — 2): 19 = 86 и 13 в остатке. В том случае, если дата указана по эре от сотворения мира, ее следует разделить на 19, и остаток определит круг луны.
Определение дат по астрономическим явлениям. В источниках, прежде всего в русских летописях, довольно часто отмечаются различные астрономические явления: солнечные и лунные затмения, кометы, падающие звезды и т. д. Известно, что астрономические явления, как правило, строго закономерны, поэтому они дают дополнительные возможности для установления или проверки лет. Астрономами составлены специальные таблицы, по которым можно с точностью до суток установить время солнечных и лунных затмений. Например, именно указание Слова о полку Игореве на солнечное затмение позволило точно установить дату похода князя Игоря на половцев. Дело в том, что этот поход летописями датировался по-разному — 6693 и 6694 гг. Затмение солнца приходилось по летописям на 1 мая, на среду. Перевод летописных дат похода на современное летосчисление дал три возможные даты: поход мог произойти в 1185 или в 1186 гг., если летопись употребляла мартовский год, или в 1184, 1185 гг., если был употреблен ультрамартовский год. Таблицы солнечных и лунных затмений показывают, что солнечное затмение произошло 1 мая 1185 г.
Важную роль для проверки или уточнениядат играют летописные сведения о различных кометах, например о комете Галлея, которая периодически возвращается в среднем через 76 лет. С точностью до суток установлено время ее прохождения через точку орбиты, ближайшую к Солнцу (перигелий), например 19 июня 912 г., 8 июня 1465 г., 5 сентября 1682 г. и т. д.
Счет времени в XX в. В 1918 г. в нашей стране был введен Григорианский календарь. 1 июля 1919 г. было введено так называемое поясное время, с конца XIX в. уже употреблявшееся в ряде стран Европы. Суть этого нововведения заключалась в следующем.
Вследствие вращения Земли с запада на восток под Солнцем в течение полного оборота Земли вокруг своей оси раньше проходят восточные меридианы. За один час Земля поворачивается на 15 градусов (360: 24 = 15). Земной шар условно разделен на 24 часовых пояса, границы которых отстоят одна от другой на 15 градусов (от О до 23-го пояса с запада на восток). Основными считаются меридианы, делящие часовые пояса пополам. Для нулевого пояса таким является Гринвичский меридиан. Таким образом, разница между местным временем (временем в конкретной точке земного шара) и поясным не превышает получаса. В некоторых случаях она может быть больше или меньше, так как не везде границы поясов отстоят от меридиана на 7, 5 градуса. Это несоответствие объясняется тем обстоятельством, что при установлении границ часовых поясов учитывались государственные границы, а также характер рельефа местности.
Значение хронологии для исторических исследований.
Изучая письменные источники, историк, прежде всего, должен проверить их подлинность и установить по возможности наиболее полную и точную их дату. Установление подлинности источника осуществляется с помощью различных вспомогательных исторических дисциплин. Правильная датировка источника в целом, его отдельных частей или отдельных сообщений и фактов невозможна без знания исторической хронологии. Достаточно привести несколько примеров, чтобы сказанное стало очевидным.
В различных изданиях, в том числе и учебного характера, можно встретить две датировки договора князя Олега с греками — 911 или 912г. Текст договора, дошедший до нас в двух летописях (Лаврентьевской и Ипатьевской), заканчивается указанием на время его составления: «Месяца сентября в 2, а в неделю 15, в лето создания мира 6420». Для точного перевода этой даты на современное летосчисление необходимо выяснить, какой счет времени (мартовский, ультрамартовский или сентябрьский) употреблен в данном случае. При мартовском счете времени договор датируется 912 г., а при ультрамартовском и сентябрьском — 911 г. Решить этот вопрос позволяет подробное указание самого текста на дату. Так как договор заключен в «неделю», т.е. в воскресенье, можно предполагать, что: 1) это воскресенье было 15-м по счету в данном году; 2) из-за небрежности переписчика 15 и 2 поменялись местами и, следовательно, имеется в виду 15 сентября, бывшее как раз вторым воскресеньем данного сентябрьского года; 3) может быть, после цифры 15 пропущено слово «индикта» или вместо «индикта» указана неделя.
Рассмотрим каждую из указанных возможностей. Первое предположение отпадает сразу же, поскольку в мартовском году 15-е воскресенье пришлось бы на июнь, а в сентябрьском — на декабрь. Второе предположение невозможно, так как воскресенье 15 сентября в сентябрьском году могло быть третьим по счету, но никак не вторым. Кроме того, по таблицам или по формуле Н.Г.Бережкова можно убедиться, что 2 сентября 6420 г. по мартовскому стилю приходилось на среду, а 15-е — на вторник, по сентябрьскому, соответственно, на понедельник и на воскресенье, но это воскресенье никак не могло быть вторым по счету.
Следовательно, можно уверенно заключить, что запись о дате договора содержит указание на индикт, а не на день недели. Индикт 6420 г. действительно 15, так как эта дата делится на 15 без остатка. Индикт 15 в данном случае указывает на сентябрьский год, так как для января — февраля и сентября — декабря мартовского года будет равен 1. 6420 г. сентябрьского стиля соответствует 911г.
Об установлении точной даты похода князя Игоря против половцов в 1185 г. говорилось выше. С помощью различных хронологических расчетов была выяснена дата битвы с монголо-татарами на реке Калке в 1223 г., которая в разных источниках датируете 6731, 6732, 6733 и 6734 гг., т.е. в зависимости от календарного стиля:
употребленного источником, была возможна датировка этого события в пределах 1222-1227 гг.
Случаи сложных и спорных датировок встречаются и при работе с источниками более позднего времени, в том числе и новейшего, поэтому знание исторической хронологии необходимо не только для историков, изучающих древнюю и средневековую историю.
|