
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка задачи. Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и
|
|
Уравнение 
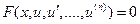 называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области
называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области 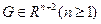 и, во всяком случае, зависит от
и, во всяком случае, зависит от 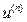 . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид
. Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид 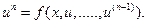 Решением этого уравнения на интервале I=[a, b] называется функция u(x).
Решением этого уравнения на интервале I=[a, b] называется функция u(x).
Решить дифференциальное уравнение у/=f(x, y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2, …, уn, что уi=F(xi)(i=1, 2, …, n) и F(x0)=y0.
Темой курсовой работы является «Сравнение трудоемкости различных методов решения дифференциальных уравнений. Метод Эйлера и метод Рунге-Кутта». Заданное уравнение:
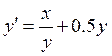 (1.1)
(1.1)
при y(0)=1 на отрезке [0; 0.5] с шагом h=0.1. Вычисления вести с тремя верными знаками.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (1.1) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка.
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов [2, с. 78]. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y' = F(x, y) (1.1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4)/6, (1.2)
где
k1 = Fk h = F(xk, yk )h,
k2 = F(xk +h/2, yk +k1 /2)h,
k3 = F(xk +h/2, yk +k2 /2)h,
k4 = F(xk +h, yk +k3)h,
k = 0,..., n-1.
h = (xf -x0)/n (1.3)
Метод Эйлера.
Решить дифференциальное уравнение у/=f(x, y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2, …, уn, что
уi=F(xi)(i=1, 2, …, n) и F(x0)=y0 (1.4)
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (1.4) с начальным условием
x=x0, y(x0)=y0 (1.5)
Требуется найти решение уравнения (1. 4) на отрезке [а, b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2, …, хn, где xi=x0+ih (i=0, 1, …, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0, 1, 2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0, 1, 2, …); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1.7), которая проходит через точку Мi. Если правая часть уравнения (1.4) в некотором прямоугольнике R{|x-x0|£ a, |y-y0|£ b}удовлетворяет условиям:
|f(x, y1)- f(x, y2)| £ N|y1-y2| (N=const), (1.6)
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
|y(xn)-yn| £ hM/2N[(1+hN)n-1], (1.7)
где у(хn)-значение точного решения уравнения (1.4) при х=хn, а уn- приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn* оценивается формулой
|yn-y(xn)|»|yn*-yn| (1.8)
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядках [2, c. 57].