
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случай1
|
|
Вариант 2
ЧАСТЬ2
C1 А:: Решите уравнение 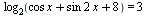 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
C2 В прямой шестиугольной призме 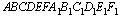 все ребра равны 1. Найдите расстояние от точки B до плоскости
все ребра равны 1. Найдите расстояние от точки B до плоскости 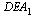 .
.
C3 Решите систему неравенств  .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в трегольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 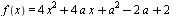 на множестве
на множестве 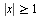 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 4
ЧАСТЬ2
C1 а) Решите уравнение 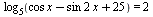 . б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
. б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
C2 В прямоугольном параллелепипеде 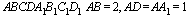 . Найдите угол между прямой
. Найдите угол между прямой 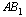 и плоскостью
и плоскостью 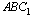 .
.
C3 Решите систему неравенств 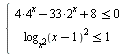 .
.
C4 Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 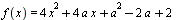 на множестве
на множестве 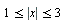 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 5
ЧАСТЬ2
C1 А:: Решите уравнение 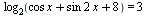 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
C2 В прямой шестиугольной призме 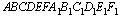 все ребра равны 1. Найдите расстояние от точки B до плоскости
все ребра равны 1. Найдите расстояние от точки B до плоскости 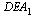 .
.
C3 Решите систему неравенств  .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в трегольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 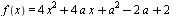 на множестве
на множестве 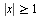 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 6
ЧАСТЬ2
C1 А:: Решите уравнение  . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [-3.5π; -2π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [-3.5π; -2π ].
C2 В прямоугольном параллелепипеде 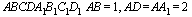 . Найдите угол между прямой
. Найдите угол между прямой 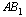 и плоскостью
и плоскостью 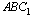 .
.
C3 Решите систему неравенств 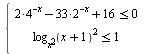 .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12.5, средняя линия трапеции равна 27.5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 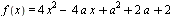 на множестве
на множестве 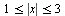 не меньше 6.
не меньше 6.
C6 Имеется 10 карточек. На них записывают по одному каждое из чисел 1, -3, 4, -5, 7, -8, 9, 10, -11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 7
ЧАСТЬ2
C1 а) Решите уравнение 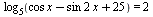 . б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
. б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
C2 В прямоугольном параллелепипеде 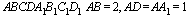 . Найдите угол между прямой
. Найдите угол между прямой 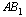 и плоскостью
и плоскостью 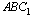 .
.
C3 Решите систему неравенств 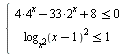 .
.
C4 Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 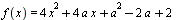 на множестве
на множестве 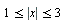 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 8
ЧАСТЬ2
C1 А:: Решите уравнение 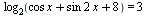 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
C2 В прямой шестиугольной призме 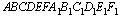 все ребра равны 1. Найдите расстояние от точки B до плоскости
все ребра равны 1. Найдите расстояние от точки B до плоскости 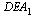 .
.
C3 Решите систему неравенств  .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в трегольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 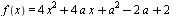 на множестве
на множестве 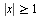 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 9
ЧАСТЬ2
C1 А:: Решите уравнение  . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [-3.5π; -2π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [-3.5π; -2π ].
C2 В прямоугольном параллелепипеде 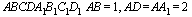 . Найдите угол между прямой
. Найдите угол между прямой 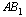 и плоскостью
и плоскостью 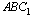 .
.
C3 Решите систему неравенств 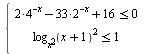 .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12.5, средняя линия трапеции равна 27.5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 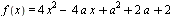 на множестве
на множестве 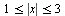 не меньше 6.
не меньше 6.
C6 Имеется 10 карточек. На них записывают по одному каждое из чисел 1, -3, 4, -5, 7, -8, 9, 10, -11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 10
ЧАСТЬ2
C1 а) Решите уравнение 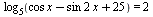 . б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
. б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
C2 В прямоугольном параллелепипеде 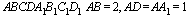 . Найдите угол между прямой
. Найдите угол между прямой 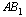 и плоскостью
и плоскостью 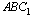 .
.
C3 Решите систему неравенств 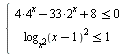 .
.
C4 Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 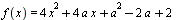 на множестве
на множестве 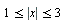 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 11
ЧАСТЬ2
C1 А:: Решите уравнение 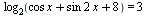 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
C2 В прямой шестиугольной призме 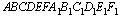 все ребра равны 1. Найдите расстояние от точки B до плоскости
все ребра равны 1. Найдите расстояние от точки B до плоскости 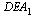 .
.
C3 Решите систему неравенств  .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в трегольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 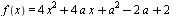 на множестве
на множестве 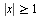 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 12
ЧАСТЬ2
C1 А:: Решите уравнение 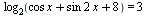 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].
C2 В прямой шестиугольной призме 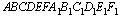 все ребра равны 1. Найдите расстояние от точки B до плоскости
все ребра равны 1. Найдите расстояние от точки B до плоскости 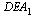 .
.
C3 Решите систему неравенств  .
.
C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в трегольник BMC.
C5 Найдите все значения a, при каждом из которых наименьшее значение функции 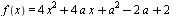 на множестве
на множестве 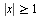 не меньше 6.
не меньше 6.
C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
А:: Может ли в результате получиться 0?
Б:: Может ли в результате получиться 1?
В:: Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 3
C1 А:: Решите уравнение 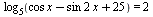 . Б:: Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
. Б:: Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].
Решение
А:: Избавимся от логарифма, учитывая его область определения:
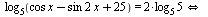
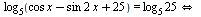
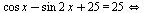
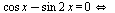
Применим формулу синуса двойного угла:
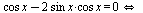
Разложим левую часть уравнения на множители:

Получим совокупность элементарных тригонометрических уравнений:
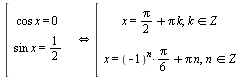
Б:: Учтём наложенные ограничения:
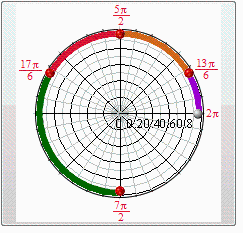

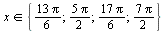
Ответ
А:: 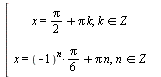 Б::
Б:: 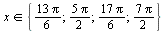
Проверка
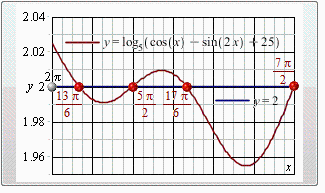
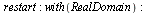
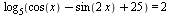
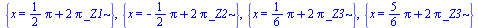
ЧАСТЬ 2 ВАРИАНТ:: 3
C2 В прямоугольном параллелепипеде 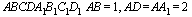 . Найдите угол между прямой
. Найдите угол между прямой 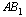 и плоскостью
и плоскостью 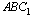 .
.
Решение
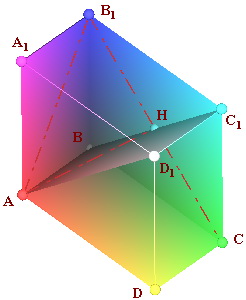
Даны измерения прямоугольного параллелепипеда:
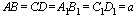
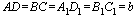
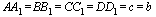
Сечением прямоугольного параллелепипеда 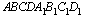 плоскостью
плоскостью 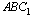 будет прямоугольник
будет прямоугольник 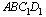 .
.
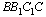 - квадрат (т.к. b = c), поэтому
- квадрат (т.к. b = c), поэтому 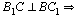
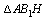 - прямоугольный.
- прямоугольный.
Искомый угол α - между прямой 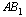 и её проекций AH на плоскость
и её проекций AH на плоскость 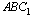 ⇒
⇒
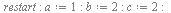
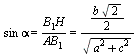
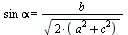 =
= 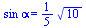 ⇒
⇒
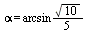
Ответ
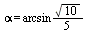
Вариант 3
C3 Решите систему неравенств 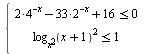 .
.
Решение
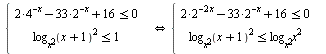
1:: Решим первое неравенство заменой:
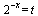
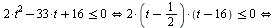
Применим теорему о знаке квадратичной функции:
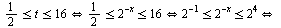
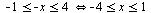
2:: Пусть 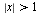 . При таком условии исходная система равносильна
. При таком условии исходная система равносильна
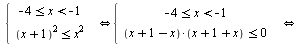
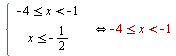
3:: Пусть 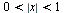 . При таком условии исходная система равносильна
. При таком условии исходная система равносильна
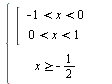

4:: Объединим решения
Ответ
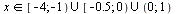
Проверка
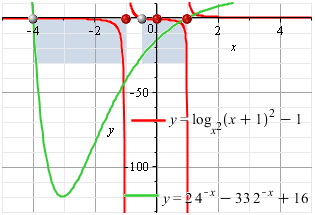

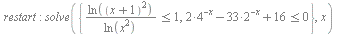
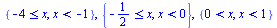
ЧАСТЬ 2 ВАРИАНТ:: 3
C4 Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12.5, средняя линия трапеции равна 27.5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
Решение
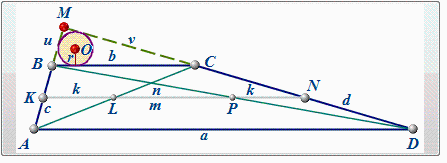
Решим задачу в общем виде, что далеко не обязательно для абитуриентов.
СЛУЧАЙ1
Дана трапеция ABCD (BC ║ AD).
Отрезок LP, соединяющий середины диагоналей трапеции, принадлежит её средней линии KN.
Пусть 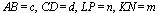
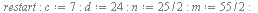
Кроме того, введём обозначения:
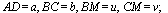
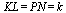 (как средние линии треугольников с общим основанием BC).
(как средние линии треугольников с общим основанием BC).
1:: 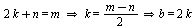
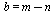 =
= 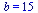
2:: Из свойства средней линии вытекает:
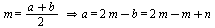
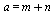 =
= 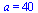
3:: Из подобия треугольников BMC и AMD имеем:
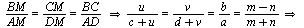
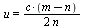 =
= 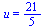
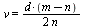 =
= 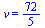
4:: Полупериметр треугольника BMC:
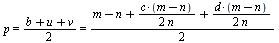
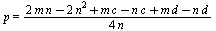 =
= 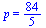
Площадь этого треугольника по формуле Герона:
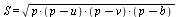
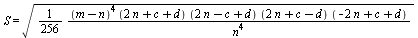
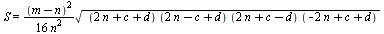
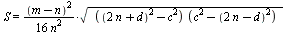 =
= 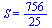
Наконец, радиус вписанной в треугольник BMC окружности:
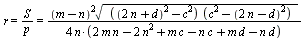
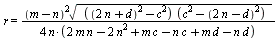 =
= 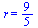
|