их к каноническому виду

Квадратичные формы и приведение

Квадратичной формой от переменных 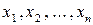называется скалярная функция векторного аргумента, которая представляет собой симметрический однородный многочлен второй степени от этих переменных

,

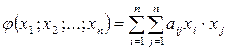где .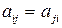

Например,

- квадратичная форма от двух переменных;

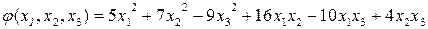- КФ от трех переменных.

Матрицей квадратичной формы называется матрица, составленная из коэффициентов квадратичной формы: .

Пример.

;

;

;

.

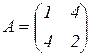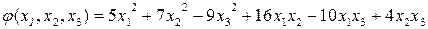Матрицы квадратичных форм – симметричные. Рангом квадратичной формы называется ранг ее матрицы. Собственными векторами квадратичной формы называются собственные векторы ее матрицы. Корни характеристического уравнения матрицы называют характеристическими числами квадратичной формы, а направления собственных векторов, соответствующих характеристическим числам, главными направлениями квадратичной формы.

Любая симметричная квадратная матрица порядка n имеет n действительных собственных значений и собственных векторов. Собственные векторы симметричной матрицы попарно ортогональны. Следовательно, собственные векторы матрицы квадратичной формы образуют базис в пространстве .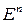

Квадратичная форма называется положительно определенной, если .

Критерий Сильвестра. Квадратичная форма является положительно определенной тогда и только тогда, когда все левые верхние угловые миноры ее матрицы положительны:

;

;

………

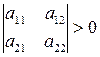Квадратичная форма отрицательно определена, если знаки ее угловых миноров чередуются, начиная с отрицательного.

Пример.

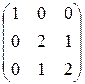- положительно определенная.

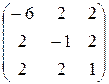- КФ знаконеопределенная.

Если обозначить матрицу-столбец из переменных ,

то, пользуясь правилом умножения матриц, квадратичную форму можно записать в виде матричного уравнения

.

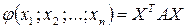Пример.

;

; ; .

.

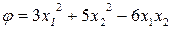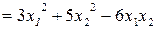Если квадратичная форма не содержит смешанных произведений переменных, говорят, что она имеет канонический вид.

.

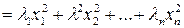Матрица, соответствующая квадратичной форме канонического вида, диагональна.

Например, ; .

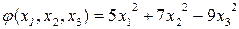Канонический вид КФ определяется неоднозначно. В то же время, можно доказать, что все канонические виды, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов. Общее число квадратов переменных равно рангу КФ. Это свойство называют законом инерции КФ.

Чтобы привести квадратичную форму 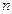переменных к каноническому виду, нужно:

1) записать матрицу квадратичной формы;

2) составить характеристическое уравнение ;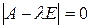

3) найти собственные значения ;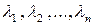

4) записать однородную систему уравнений 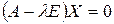и найти собственные векторы матрицы ;

5) составить ортогональную матрицу перехода T, столбцами которой являются координаты нормированных собственных векторов;

6) составить новую матрицу квадратичной формы канонического вида по формуле: .

7) записать канонический вид квадратичной формы

Пример.Привести к каноническому виду квадратичную форму:

.

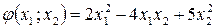Решение.

Запишем матрицу квадратичной формы:

;

Составим и решим характеристическое уравнение:

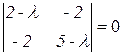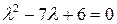, ; - собственные значения. Решим систему уравнений:

Подставляя сюда и 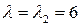, найдем собственные векторы и 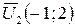. Нормируя собственные векторы 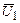и , находим векторы, образующие новый ортонормированный базис и определяющие главные направления квадратичной формы:

.

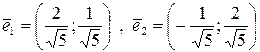Ортогональная матрица перехода 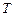имеет вид

; .

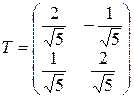Тогда - диагональный вид матрицы в найденном ортонормированном базисе.

Итак, ортогональное преобразование переменных

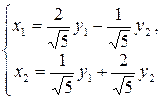
приводит данную квадратичную форму к каноническому виду:

.

Здесь важно при переходе к новому базису сохранить ориентацию системы координат. Если , то ориентация сохраняется, если же , то ориентацию новых осей следует изменить. Для этого достаточно сменить направление одного собственного вектора, умножив его координаты на –1.