Взаимное расположение прямых на плоскости.

Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?

Во-первых, две прямые на плоскости могут совпадать.

Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.

Во-вторых, две прямые на плоскости могут пересекаться.

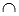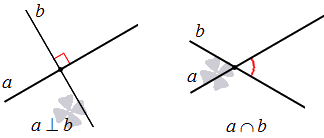
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись 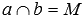означает, что прямые а и b пересекаются в точке М. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми. Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b, то можно использовать краткую запись .

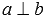В-третьих, две прямые на плоскости могут быть параллельными.

Две прямые на плоскости называются параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение 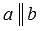. Для более полной информации смотрите статью параллельные прямые, параллельность прямых.

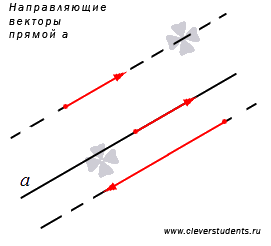
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой. В статьенаправляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.

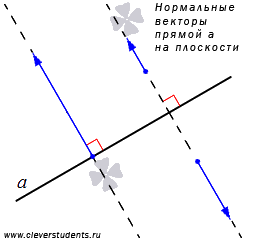
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой. О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости.

Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.

Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:

· если две прямые параллельны третьей прямой, то они параллельны между собой;

· если две прямые перпендикулярны третьей прямой, то они параллельны между собой;

· если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.

К началу страницы