
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цель работы:определение скорости звуковой волны в воздухе на основе интерференции волн.
|
|
Нижегородский государственный технический университет
им. Р. Е. Алексеева
Лабораторная работа №3-5
«Интерференция звуковых волн»
Выполнил:
Проверил:
Нижний Новгород, 2014
Цель работы: определение скорости звуковой волны в воздухе на основе интерференции волн.
Приборы и оборудование: звуковой генератор электрических колебаний; замкнутая труба, по которой распространяется звук (труба Квинке) со встроенными в нее динамиком и микрофоном; вольтметр
Теоретическая часть.
1. Природа звуковых волн в воздухе. Уравнение волны. Параметры, описывающие волну.
 Волнами называются возмущения, распространяющиеся в пространстве.
Волнами называются возмущения, распространяющиеся в пространстве.
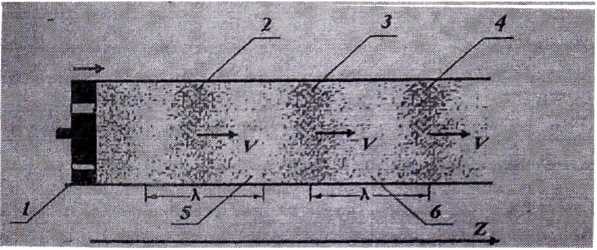
Рис. 1
Звуковая волна в воздухе может возникнуть, если, например; мембрана (1 на рис. 1) совершает гармонические колебания относительно положения равновесия вдоль оси Z.. В воздухе возникают сменяющие друг друга области сжатия (2, 3, 4) и разрежения (5, 6), которые перемещаются вдоль оси Z со скоростью звука v. При этом регулярного потока частиц не наблюдается. Области сжатия и разрежения образуются вследствие того, что в дополнение к хаотическому тепловому движению молекулы воздуха совершают упорядоченные колебательные движения, вызванные колебанием мембраны. Следовательно, в звуковой волне воздух не перемещается вместе с волной, а перемещается лишь возмущение (изменение) давления 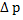 по отношению к равновесному давлению (атмосферному давлению ратм). При ограниченной мощности звука
по отношению к равновесному давлению (атмосферному давлению ратм). При ограниченной мощности звука 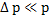 атм.
атм.
Уравнение, описывающее плоскую гармоническую волну, бегущую вдоль оси z, имеет вид:
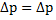 м * cos(
м * cos(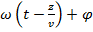 0) (1)
0) (1)
Волна, в отличии от колебаний - функция не только времени, но и координаты.
В уравнении (1) 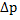 м [Па] - амплитуда, т.е. максимальное отклонение давления от равновесного значения;
м [Па] - амплитуда, т.е. максимальное отклонение давления от равновесного значения;  - мгновенное значение возмущения давления в данной точке z в данный момент времени t;
- мгновенное значение возмущения давления в данной точке z в данный момент времени t;
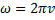 - круговая частота;
- круговая частота;
v - частота колебаний.
Человек слышит звук в диапазоне частот от 16 Гц до 20 кГц. Звуковые волны с частотами ниже 16 Гц (инфразвук) и выше 20 кГц (ультразвук) не воспринимаются человеческим ухом.
Аргумент косинуса 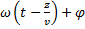 0=
0= 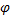 - фаза волны,
- фаза волны, 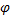 0 - ее начальная фаза. Периодическая функция косинус с периодом 2
0 - ее начальная фаза. Периодическая функция косинус с периодом 2 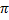 описывает периодическое возмущение давления во времени и пространстве.
описывает периодическое возмущение давления во времени и пространстве.
Период Т- время, за которое совершается полный цикл колебаний в данной точке пространства, причем Т = 
Длина волны λ - расстояние между двумя соседними максимумами или минимумами возмущения. Если расстояние между точками волнового поля равно длине волны, то возмущения параметров, характеризующие состояние среды, колеблются с разностью фаз 2л (см. рис). Другими словами, это расстояние, на которое распространяется гармоническая волна за время, равное периоду колебаний Т:
λ = 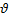 T, (2)
T, (2)
Поскольку Т = 1/ v формулу (2) можно представить как
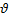 = λ v, (3)
= λ v, (3)
Следовательно, если измерить λ и v, то по формуле (3) можно определить скорость звука.
Возмущение среды может быть описано не только параметром 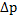 , но и другими. Возмущения плотности
, но и другими. Возмущения плотности  ρ, температуры
ρ, температуры 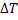 , смещение частиц
, смещение частиц  ζ относительно положения равновесия также будут описываться гармонических составляющих. Волновое возмущение, не изменяющее в процессе своего распространения форму, во всех случаях зависит от параметра
ζ относительно положения равновесия также будут описываться гармонических составляющих. Волновое возмущение, не изменяющее в процессе своего распространения форму, во всех случаях зависит от параметра 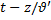 если волна распространяется со скоростью
если волна распространяется со скоростью 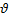 по оси z, или от параметра
по оси z, или от параметра 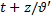 если против оси г.
если против оси г.
Звуковая волна в газе - продольная (см. рис.1), смещение частиц от положения равновесия происходит вдоль направления распространения волны. В твердом теле, где может возникать деформация сдвига, могут существовать как продольные, так и поперечные волны (смещение частиц поперек скорости распространения волны). Уравнение (1) описывает плоскую волну, возмущения в которой зависят лишь от одной координаты.
Скорость звука в воздухе при нормальных условиях - около 330 м/с. Скорость продольных волн в воде -1500 м/с, в стали - 5800 м/с. Поскольку воздух при нормальных условиях близок к идеальному газу, скорость звука можно оценить по формуле (1).
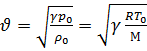 (4)
(4)
где 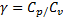 - отношение теплоемкостей при постоянных давлениях и объеме;
- отношение теплоемкостей при постоянных давлениях и объеме; 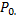
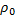 , Т0 - невозмущенные давление, плотность и температура среды; R - универсальная газовая постоянная, М - молярная масса. С увеличением температуры скорость звука в газах растет.
, Т0 - невозмущенные давление, плотность и температура среды; R - универсальная газовая постоянная, М - молярная масса. С увеличением температуры скорость звука в газах растет. 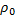 = 1, 29 кг/м3
= 1, 29 кг/м3
р0 = О, 1 МПа; Т0 = 3ОО К; R =8, 314 Дж/ (К*моль).
8, 314 Дж/(К • моль).
2. Понятие об интерференции. Разность хода волн. Условие максимума при интерференции.
Интерференция - процесс сложения волн, при котором результирующая интенсивность отличается от суммы интенсивностей складываемых волн. Интенсивность пропорциональна квадрату амплитуды волны. Интерференцию можно реализовать, если складываемые волны когерентны. Волны когерентны, если имеют разность фаз, не зависящую от времени в любой точке волнового поля.
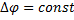
Монохроматические волны одной и той же частоты всегда интерферируют между собой, т.е. когерентны.
При сложении двух волн амплитуда результирующего колебания будет максимальна в том случае, если разность фаз принимает значение (1)
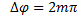 (5)
(5)
Здесь т= 0, 1, 2... Пусть две волны прошли разные пути z1 и z2 от одного источника до точки наблюдения. Величину
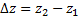 (6)
(6)
называют разностью хода волн. В соответствии с (6) и (2), если волны распространяются в одной среде,
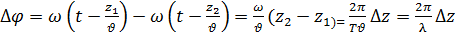 .
.
Соотношение
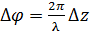 (7)
(7)
дает связь разности фаз и разности хода волн. Следовательно, условие максимума (6) можно выразить через разность хода
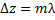 (8)
(8)
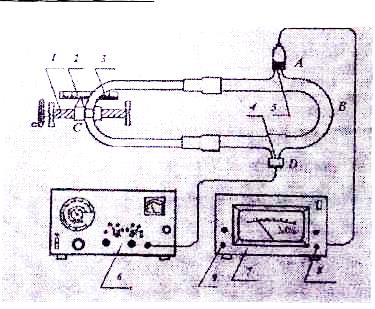
Схема установки.
|
Установка содержит две изогнутые трубы ABD и ACD, близкие по диаметру и вставленные одна в другую так, что их можно раздвигать с помощью винта 1 и тем самым измерять длину участка ACD (т.е. z2). Для определения перемещения трубы имеется указатель 2 и миллиметровая шкала 3 длиной 20 см. Такое устройство называют трубой Квинке. В динамик 4 поступает электрический сигнал от звукового генератора 6. Частота сигнала отсчитывается по внешней шкале генератора (0-г5000 Гц). Динамик преобразует его в звуковую волну той же частоты, которая, распространяясь по трубе, достигает микрофона. Сигнал с микрофона 5 поступает для измерения на вольтметр 7. У вольтметра имеется две управляющие кнопки. Кнопка 8 предназначена для измерения на вольтметр 7. У вольтметра имеется две управляющие кнопки. Кнопка 8 предназначена для включения сети, кнопка 9 - для включения прибора в действие.
Ход работы:
Для проведения измерений преподавателем задается определенный диапазон частоты. Выбрав определенную частоту, перемещают левую трубу от крайнего левого положения вправо, наблюдая по показаниям вольтметра, как изменится сигнал в точке А. При таком перемещении z1 в формулах (6), (8) останется неизменным, а z2 уменьшается. Вначале находят первое положение L1 шкалы 3, при котором сигнал максимален. Для этого положения шкалы соотношение (8) запишется:
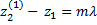 (8а)
(8а)
Будем перемещать трубу вправо до нового положения L2, при котором вновь будет максимум. Как видно из конструкции, каждому смещению по шкале 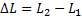 соответствует удвоенное уменьшение z2. При этом величина m уменьшается на единицу. Таким образом, для положения, в котором наблюдается второй максимум, выражение (8а) можно переписать:
соответствует удвоенное уменьшение z2. При этом величина m уменьшается на единицу. Таким образом, для положения, в котором наблюдается второй максимум, выражение (8а) можно переписать:
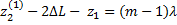 (8б)
(8б)
Вычтя (8б) из (8а), получим формулу экспериментального определения длины волны.
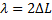 (9)
(9)
Зная 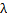 и частоту звукового генератора v, по формуле (3) найдем скорость звука.
и частоту звукового генератора v, по формуле (3) найдем скорость звука.
Расчеты-
Формулы: 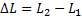 расстояние между соседними положениями указателями
расстояние между соседними положениями указателями
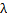 = 2
= 2 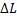
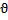 =
= 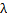 v
v
| № n/n | v, Гц | L, мм |  L, мм L, мм
| 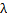 , м , м
| v, м/с | < 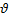 >, м/с >, м/с
|
| № п/п | V, Гц | L, мм |  L, мм L, мм
| 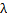 , м , м
| 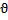 , m/c , m/c
| < 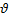 >, м/с >, м/с
|
| № п/п | v, Гц | L, мм |  L, мм L, мм
| 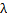 , м , м
| 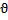 , м/с , м/с
| < 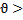 , м/с , м/с
|
Подсчёт погрешности измерения скорости:
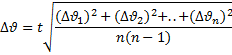
где:
n – число измерений; 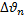 –отклонение от среднего значения
–отклонение от среднего значения 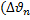 =
= 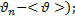 t-коэффициент Стьюдента (t=2).
t-коэффициент Стьюдента (t=2).
Вывод:
|