Досрочный26. 04. 2012v2

ДОСРОЧНЫЙ26.04.2012V1

ЧАСТЬ1

B1 Пачка сливочного масла стоит 64 рубля. Пенсионерам магазин делает скидку 15%. Сколько рублей заплатит пенсионер за две пачки масла?

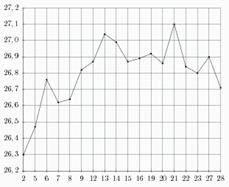
B2 На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 2 февраля по 28 февраля 2002 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа курс евро впервые был равен 26, 8 рубля.

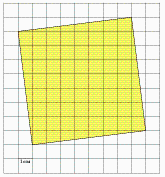
B3 Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.) Ответ дайте в квадратных сантиметрах.

B4 Семья из трех человек планирует поехать из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 900 рублей. Автомобиль расходует 14 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 20, 5 рубля за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?

B5 Найдите корень уравнения .

B6 Найдите вписанный угол, опирающийся на дугу, которая составляет 17/36 окружности. Ответ дайте в градусах.

B7 Найдите значение выражения .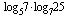

B8 На рисунке изображен график дифференцируемой функции y = f (x) и отмечены девять точек на оси абсцисс: 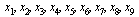. В скольких из этих точек производная функция f (x) положительна?

B9 В правильной четырехугольной пирамиде SABCD точка O - центр основания, S вершина, SO = 15, SD = 17. Найдите длину отрезка BD.

B10 В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.

B11 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

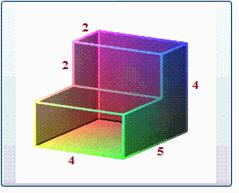
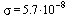B12 Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: , где - постоянная, площадь S измеряется в квадратных метрах, а температура T - в градусах Кельвина. Известно, что некоторая звезда имеет площадь 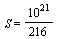кв.м, а излучаемая ею мощность P не менее Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.

B13 В сосуд, содержащий 4 литров 16-процентного водного раствора некоторого вещества, добавили 4 литров воды. Сколько процентов составляет концентрация получившегося раствора?

B14 Найдите наибольшее значение функции на отрезке [-5.5; 0]

ЧАСТЬ2

C1 а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 3.5π ].

C2 В прямоугольном параллелепипеде 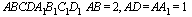. Найдите угол между прямой и плоскостью .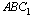

C3 Решите систему неравенств .

C4 Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.

C5 Найдите все значения a, при каждом из которых наименьшее значение функции на множестве не меньше 6.

C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?

ДОСРОЧНЫЙ26.04.2012V2

ЧАСТЬ1

B1 Пачка сливочного масла стоит 50 рублей. Пенсионерам магазин делает скидку 15%. Сколько рублей заплатит пенсионер за две пачки масла?

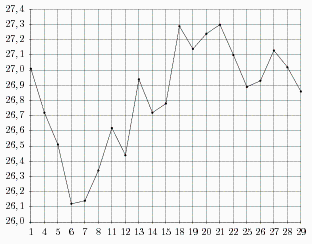
B2 На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 1 по 29 сентября 2001 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа курс евро впервые был равен 26, 5 рубля.

B3 Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.) Ответ дайте в квадратных сантиметрах.

B4 Семья из трех человек планирует поехать из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 780 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?

B5 Найдите корень уравнения .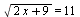

B6 Найдите вписанный угол, опирающийся на дугу, которая составляет 7/36 окружности. Ответ дайте в градусах.

B7 Найдите значение выражения .

B8 На рисунке изображен график дифференцируемой функции y = f (x) и отмечены девять точек на оси абсцисс: 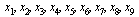. В скольких из этих точек производная функция f (x) отрицательна?

B9 В правильной четырехугольной пирамиде SABCD точка O - центр основания, S вершина, SO = 35, SA = 91. Найдите длину отрезка AC.

B10 В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

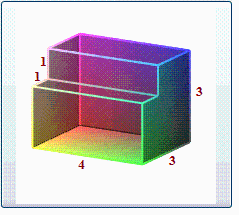
B11 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

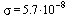B12 Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: , где - постоянная, площадь S измеряется в квадратных метрах, а температура T - в градусах Кельвина. Известно, что некоторая звезда имеет площадь кв.м, а излучаемая ею мощность P не менее 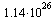Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.

B13 В сосуд, содержащий 10 литров 26-процентного водного раствора некоторого вещества, добавили 3 литров воды. Сколько процентов составляет концентрация получившегося раствора?

B14 Найдите наибольшее значение функции на отрезке [-2.5; 0]

ЧАСТЬ2

C1 а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку [1.5π; 3π ].

C2 В прямоугольной шестиугольной призме 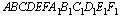все ребра равны 1. Найдите расстояние от точки B до плоскости .

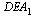C3 Решите систему неравенств .

C4 Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.

C5 Найдите все значения a, при каждом из которых наименьшее значение функции 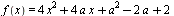на множестве 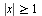не меньше 6.

C6 Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записывают на карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?