Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Среднее квадратичное отклонение
|
|
Обработка ряда измерений
Результаты отдельных наблюдений
| 75, 3 | 75, 7 | 76, 1 | 76, 5 | 76, 8 | 77, 2 | 77, 5 | 77, 9 | 78, 4 | 78, 7 |
| 78, 7 | 78, 7 | 78, 7 | 78, 8 | 78, 8 | 78, 8 | 78, 9 | 78, 9 | 79, 1 | |
| 79, 2 | 79, 3 | 79, 7 | 79, 9 | 80, 2 | 80, 5 | 80, 9 | 81, 2 | 81, 6 | 81, 9 |
| мА |
Ищем оценку истинного значения – это среднее значение (точечная оценка) 
:
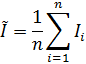
Сумма результатов наблюдений = 2362, 9
Количество наблюдений=30
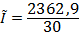=78, 76
1) Найдем наибольшее и наименьшее значение
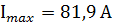
2) Определим ширину диапазона
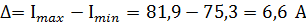
3) Запишем результаты в виде такой таблицы
| Значение I [мА] | Количество |
| 75, 3 | |
| 75, 7 | |
| 76, 1 | |
| 76, 5 | |
| 76, 8 | |
| 77, 2 | |
| 77, 5 | |
| 77, 9 | |
| 78, 4 | |
| 78, 7 | |
| 78, 8 | |
| 78, 9 | |
| 79, 1 | |
| 79, 2 | |
| 79, 3 | |
| 79, 7 | |
| 79, 9 | |
| 80, 2 | |
| 80, 5 | |
| 80, 9 | |
| 81, 2 | |
| 81, 6 | |
| 81, 9 |
1) Выбираем число интервалов
k=10 (n=30)
2) Найдем границы интервалов
3)
4) Наедем число попаданий в интервал
| Номер интервала i | Интервал | Число попаданий ni |
| 1. | 75, 3 -75, 96 | |
| 2. | 75, 96-76, 62 | |
| 3. | 76, 62-77, 28 | |
| 4. | 77, 28-77, 94 | |
| 5. | 77, 94-78, 6 | |
| 6. | 78, 6-79, 26 | |
| 7. | 79, 26-79, 92 | |
| 8. | 79, 92-80, 58 | |
| 9. | 80, 58-81, 24 | |
| 10. | 81, 24-81, 9 |
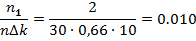
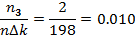
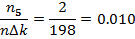
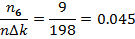
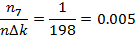
= 0, 015
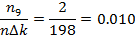
Среднее значение измеряемой величины: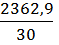 
= 78, 76333
Дисперсия
Диспе́ рсия случа́ йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания
Дисперсия рассчитывается по формуле:
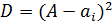
Значения дисперсии приведены в таблице
| 11, 99468 | 9, 384011 | 7, 093344 | 5, 122678 | 3, 854678 | 2, 444011 | 1, 596011 | 0, 745344 | 0, 132011 | 0, 004011 |
| 0, 004011 | 0, 004011 | 0, 004011 | 0, 001344 | 0, 001344 | 0, 001344 | 0, 018678 | 0, 018678 | 0, 056011 | 0, 113344 |
| 0, 190678 | 0, 288011 | 0, 877344 | 1, 292011 | 2, 064011 | 3, 016011 | 4, 565344 | 5, 937344 | 8, 046678 | 9, 838678 |
Среднее квадратичное отклонение
Среднее квадратическое отклонение – это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
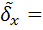1, 64
Точечная оценка среднеквадратического отклонения рассчитывается по формуле:
Точечная оценка среднеквадратического отклонения =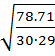 
=0.30
Формула для доверительного интервала
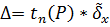
Из таблицы Стьюдента-Фишера
| |
| P | |
| n | 0.99 |
| 2.75 |
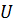=78.7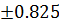 
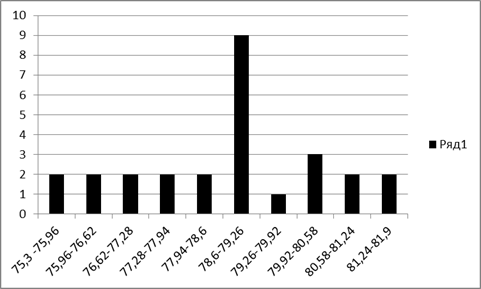
Для среднего значения: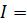 
78.7 
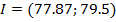
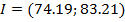
Гистограмма дифференциальной функции распределения результатов отдельных измерений
Гистограмма — способ графического представления табличных данных.
|