
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция света. 1. Монохроматические волны: Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы
|
|
1. Монохроматические волны: Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте. Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой. Бегущая монохроматическая волна: Вектор Умова-Пойнтинга S= [ExH] — вектор, направление которого совпадает с направлением распространения энергии в электромагнитной волне, а модуль |S| равен потоку энергии. Стоячая монохроматическая волна: Стоячая монохроматическая волна — волна, формирующаяся при распространении двух плоских монохроматических электромагнитных волн одинаковой поляризации навстречу друг другу.
На практике чисто монохроматическая волна не осуществима, так как должна была бы быть бесконечной - прежде всего, во времени. Реальные процессы излучения ограничены во времени, и поэтому под монохроматической обычно понимается волна с очень узким спектром. Чем уже интервал, в котором находятся частоты реальной волны, тем «монохроматичнее» излучение. В природе и технике наиболее близко к монохроматическому излучение отдельных линий спектров испускания свободных атомов и молекул. Эти линии соответствуют переходу атома из состояния с большей энергией в состояние с меньшей, а частоты соответствующих монохромных волн равны разнице уровней энергии, поделённой на постоянную Планка.
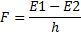
2. Когерентные световые волны: В физике когерентностью называется скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.
Классический пример двух когерентных колебаний — это два синусоидальных колебания одинаковой частоты.
Когерентность волны означает, что в различных точках волны осцилляции происходят синхронно, то есть разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем. Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (то есть нескоррелированных) излучателей.
Изучение когерентности световых волн приводит к понятиям временно́ й и пространственной когерентности.
Временная когерентность волны характеризует сохранение взаимной когерентности при временном отставании одного из таких лучей по отношению к другому. При этом мерой временной когерентности служит время когерентности – максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность ещё сохраняется. Временная когерентность определяется степенью монохроматичности.
Простра́ нственная когере́ нтность — когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны.
Без когерентности невозможно наблюдать такое явление, как интерференция.
Радиус когерентности — расстояние, при смещении на которое вдоль псевдоволновой поверхности, случайное изменение фазы достигает значения порядка π.
3. Интерференция света и методы её наблюдения: Интерференция света, сложение световых волн, при котором обычно наблюдается характерное пространственное распределение интенсивности света (интерференционная картина) в виде чередующихся светлых и тёмных полос вследствие нарушения принципа сложения интенсивностей. Некоторые явления И. с. наблюдались ещё И. Ньютоном, но не могли быть объяснены с точки зрения его корпускулярной теории. Правильное объяснение И. с. как типично волнового явления было дано в начале 19 в. Т. Юнгом и О. Френелем. И. с. возникает только в случае, если разность фаз постоянна во времени, т. е. волны когерентны.
Зеркала Фринеля: До создания лазеров когерентные световые пучки могли быть получены только путём разделения и последующего сведения лучей, исходящих из одного и того же источника света. При этом разность фаз этих колебаний постоянна и определяется только разностью путей, проходимых лучами, или разностью хода D. Существует несколько способов создания когерентных пучков света. Например, в опыте Френеля (рис. 1) два плоских зеркала I и II, образующих двугранный угол, близкий к 180°, дают два мнимых изображения S1 и S2 источника S. На экране AB получается светлая полоса при разности хода D лучей S1M и S2M, равной чётному числу полуволн, и тёмная полоса — при D, равной нечётному числу полуволн.

Метод Юнга: Другой способ был предложен Юнгом (рис. 2). Свет из отверстия S падает на экран AB с двумя отверстиями (или щелями) S1 и S2. И. с. наблюдается на экране CD. Расстояние между соседними светлыми или тёмными интерференционными полосами Dх " l/a, где a — угол S1MS2, под которым сходятся интерферирующие лучи.
4. Расчёт интерференционной картины – условия минимумов и максимумов: Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми, прорезанные в плоском непрозрачном экране (рис. 4.3a). Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления.

Рис. 4.3а
Область, в которой волны источников перекрываются, называется полем интерференции. В поле интерференции имеются места, где волны источников будут складываться в фазе. В этих местах будут отмечаться максимумы интенсивности электромагнитного поля. Там же, где волны будут складываться в противофазе - минимальная интенсивность. Если в поле интерференции поместить непрозрачный экран, то будет наблюдается чередование светлых и тёмных полос (рис. 4.3a), представляющие собой интерференционную картину. Параметрами интерференционной картины являются положение её максимумов и минимумов, а также связанная с ними ширина полос интерференционной картины (рис. 4.3a).
В соответствии с (4.4a) для расчёта этих величин надо найти разность фаз излучаемых источниками волн в точке наблюдения, расположенной на экране. Как показано в главе 3, для расчёта надо определить оптическую разность хода (треугольник) волн от первого и второго источников (рис. 4.3a) до точки наблюдения, поскольку

где n - показатель преломления среды, в которой распространяются электромагнитные волны; l1, l2- расстояния, проходимые волнами соответственно от первого и второго источников (рис. 4.3a) до точки наблюдения; “лямбда”- длина волны.
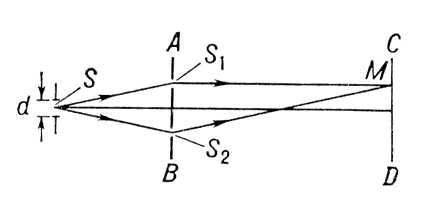
5. Интерференция света в тонких плёнках: Наблюдаемое в природе радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах) объясняется интерференцией света, возникающей в результате отражения света от передней и задней поверхностей пленки. На рисунке 17.9 изображена тонкая плоскопараллельная прозрачная пленка, на которую падают лучи света. В точке О свет частично отразится от верхней поверхности пленки (волна 1′), а частично
преломится и отразится от задней ее поверхности в точке С и, преломившись в точке В, выйдет в воздух параллельно волне 1. Волны 1′ и 1′ ′ когерентны.
Если на пути этих лучей поставить собирающую линзу, то они будут накладываться в ее фокальной плоскости и давать интерференционную картину, которая определяется их оптической разностью хода Δ =n2(OC+CB)− n1⋅ OA±λ 2 где член λ 2 — обусловлен потерей полуволны при отражении света от границы раздела оптически более плотной среды. Если n2> n1, то потеря полуволны произойдет в точке О, и этот член будет
со знаком " плюс"
Δ =n2(OC+CB)− n1(OA− λ /2)
Если n2< n1, то потеря полуволны произойдет в точке С, и он будет иметь знак " минус"
Δ =n2(OC+CB− λ 2)− n1OA
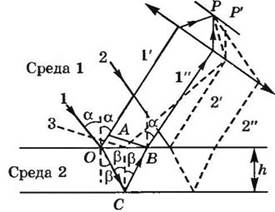
6. Полосы равной толщины: Полосы равной толщины один из эффектов оптики тонких слоев (См. Оптика тонких слоёв), в отличие от полос равного наклона (См. Полосы равного наклона), наблюдаются непосредственно на поверхности прозрачного слоя переменной толщины (рис. 1). Возникновение П. р. т. обусловлено интерференцией света (См. Интерференция света), отражённого от передней и задней границ слоя (П. р. т. в отражённом свете), или света, проходящего прямо через слой, с дважды отражённым на его границах (П. р. т. в проходящем свете). Полосами в строгом смысле (отчётливыми, попеременно тёмными и светлыми) обычно являются лишь П. р. т. монохроматическом свете (См. Монохроматический свет) или близком к нему (свете, длины волн λ которого заключены в сравнительно небольшом интервале). При этом максимумы и минимумы освещённости полос совпадают с линиями на поверхности слоя, по которым Разность хода интерферирующих лучей одинакова и равна целому числу λ /2. На этих линиях одинакова геометрическая толщина слоя — отсюда название «П. р. т.». При освещении белым светом (См. Белый свет) наложение П. р. т., отвечающих лучам с разными λ, создаёт сложную радужно-цветовую картину, в которой П. р. т. лучей с отдельными λ зачастую неразличимы. П. р. т. обусловливают радужную окраску тонких плёнок (мыльных пузырей, масляных и бензиновых пятен на воде, плёнок окислов на металлах, в частности Цвета побежалости, и пр.). Их используют для определения микрорельефа тонких пластинок и плёнок (рис. 2), в ряде Интерферометров и др. устройств для точных измерении (см., например, Ньютона кольца и рис. к этой статье; кольца Ньютона — частный пример П. р. т.).
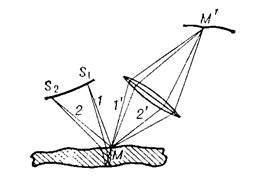
Рис. 1. Разность хода интерферирующих лучей, отражённых от верхней и нижней границ тонкого слоя, зависит от углов падения освещающих лучей. Однако разброс этих углов даже в случае протяжённых источников света обычно столь невелик, что разность хода, приобретаемая в точке М слоя лучами 1—1' и 2—2'; которые испущены разными участками (S1 и S2) источника, практически одинакова. Поэтому полосы равной толщины локализованы непосредственно на поверхности слоя и их можно наблюдать без вспомогательных оптических устройств (линза на рис. может быть хрусталиком глаза). М' — точка на сетчатке глаза (или — при использовании дополнительной линзы — на экране), где фокусируется изображение точки М поверхности слоя, т. е, одной из точек линии равной толщины.
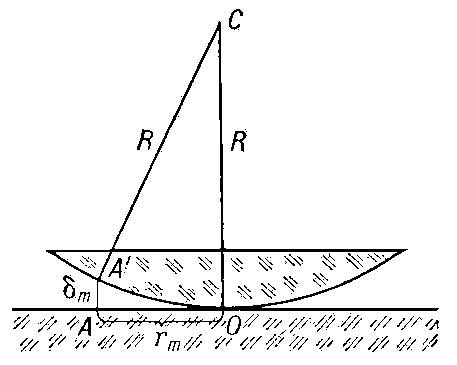
7. Кольца ньютона: Ньютона кольца интерференционные Полосы равной толщины в форме колец, расположенные концентрически вокруг точки касания двух поверхностей (двух сфер, плоскости и сферы и т.д.). Впервые описаны в 1675 И. Ньютоном. Интерференция света происходит в тонком зазоре (обычно воздушном), разделяющем соприкасающиеся тела; этот зазор играет роль тонкой плёнки, см. Оптика тонких слоев (См. Оптика тонких слоёв). Н. к. наблюдаются и в проходящем и — более отчётливо — в отражённом свете. При освещении монохроматическим светом (См. Монохроматический свет) длины волны Л, Н. к. представляют собой чередующиеся тёмные и светлые полосы. Светлые возникают в местах, где зазор вносит Разность хода между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся поверхностей (в отражённом свете), равную целому числу λ. Тёмные кольца образуются там, где разность хода лучей равна целому нечётному числу λ /2. Разность хода определяется оптической длиной пути (См. Оптическая длина пути) луча в зазоре и изменением фазы световой волны при отражении (см. Отражение света). Так, при отражении от границы воздух — стекло фаза меняется на π, а при отражении от границы стекло — воздух остаётся неизменной. Поэтому в случае двух стеклянных поверхностей т-е тёмное Н. к. в отражённом свете соответствует разности хода mλ (т. е. толщине зазора dm = mλ /2), где m — целое число. При касании сферы и плоскости (рис. 1) rm = (mλ R)1/2. По теореме Пифагора, для треугольников с катетами rп и rm R2 = (R — λ m/2)2 + rn2 и R2 = (R — λ m/2)2 + r2m, откуда следует — в пренебрежении очень малыми членами (mλ /2)2 и (nλ /2)2 и др.— часто используемая формула для Н. к.: R = (rn2 — r2m)/λ (n — m). Эти соотношения позволяют с хорошей точностью определять λ по измеренным rm и rп либо, если λ известна, измерять радиусы поверхностей линз (рис. 2). Н. к. используются также для контроля правильности формы сферических и плоских поверхностей (рис. 3). При освещении немонохроматическим (например, белым) светом Н. к. становятся цветными, причём чередование цветов в них существенно отличается от обычного радужного из-за переналожения систем колец, соответствующих разным т. Наиболее отчётливо Н. к. наблюдаются при использовании сферических поверхностей малых радиусов кривизны (толщина зазора мала на большем расстоянии от точки касания).
8. Полосы равного наклона: ПОЛОСЫ РАВНОГО НАКЛОНА система чередующихся светлых и тёмных полос, наблюдаемая на экране при освещении прозрачного слоя п о с т о я н н о й т о л щ и н ы (плоскопараллельной пластинки) непараллельным пучком монохроматич. излучения. Каждая полоса создаётся лучами света S и S1 (рис.), падающими на поверхность слоя под одним и тем же углом (р. Появление П. р. н. обусловлено интерференцией света, отражённого «т передней и задней границы пластинки. П. р. н. локализованы в бесконечности и для их наблюдения интерферирующие лучи собирают с помощью линзы L на экран Э или фотопластинку.

Схема наблюдения полос равного наклона. Лучи S и S1, падающие под одним углом, собираются линзой в одной точке О. Лучи, падающие под др. углом (напр., S'), собираются линзой в др. точке О'.
9. Просветлённая оптика: Просветление оптики уменьшение Отражения коэффициентов поверхностей оптических деталей путём нанесения на них одной или нескольких непоглощающих плёнок. Без таких (просветляющих) плёнок потери на отражение света могут быть значительными; так в видимой области спектра (длина волны λ = 400—700 нм) даже при нормальном падении лучей на границе воздух — оптическая среда они могут составлять до 10% от интенсивности падающего излучения (рис. 1); см. также Отражение света, Френеля формулы). В системах с большим числом поверхностей, например в сложных Объективах, потери света могут достигать 70% и более. Многократное отражение от преломляющих поверхностей вызывает появление внутри приборов рассеянного света, что ухудшает качество изображений, формируемых оптическими системами приборов. Эти нежелательные явления устраняются с помощью П. о., которое является одним из важнейших применений оптики тонких слоев (См. Оптика тонких слоёв) (см. ниже об основных классах веществ, используемых в качестве материалов для просветляющих плёнок, и способах нанесения плёнок). ветляющих плёнок, и способах нанесения плёнок).
П. о. — результат интерференции света (См. Интерференция света), отражаемого от передних и задних границ просветляющих плёнок; она приводит к взаимному «гашению» отражённых световых волн и, следовательно, к усилению интенсивности проходящего света. При углах падения, близких к нормальному, эффект П. о. максимален, если толщина тонкой плёнки равна нечётному числу четвертей длины световой волны в материале плёнки, а Преломления показатель (ПП) плёнки удовлетворяет равенству n22 = n1n3, где n1 и n3 — ПП сред, граничащих с плёнкой (часто первой средой является воздух). Отражённый свет ослабляется тем сильнее, чем больше разность n3 — n2; если же и n2 > n3, то интерференция отражённых от границ плёнки лучей, напротив, усилит интенсивность отражённого света.
Изменяя толщину просветляющей плёнки, можно сместить минимум отражения в различные участки спектра. Покрытия с минимальным отражением в жёлтой области (λ = 555 нм, область наибольшей чувствительности человеческого глаза) наносят на объективы, применяемые в черно-белой фотографии; в отражённом свете их поверхности имеют пурпурный оттенок (т. н. голубая оптика). В просветлённых объективах для цветной фотографии отражение минимально в голубой области спектра; оттенок их поверхностей — янтарный. Для деталей из стекла с низким ПП П. о. однослойными плёнками недостаточно эффективно. Применение двухслойных просветляющих плёнок позволяет почти полностью устранить отражение света от поверхности детали-подложки независимо от её ПП, но лишь в узкой области спектра. Трёхслойные просветляющие плёнки дают возможность получить равномерно низкое (Просветление оптики 0, 5%) отражение в широкой спектральной области, например во всём видимом диапазоне (рис. 3). Двух- и трёхслойные покрытия используют для П. о., работающей в ультрафиолетовой области, где из-за низкого значения n3 однослойные покрытия малоэффективны. Теоретически наилучшее П. о. в широкой области спектра может быть достигнуто с помощью неоднородных просветляющих плёнок, значение ПП которых плавно меняется от n подложки до n окружающей среды.
В практически получаемых неоднородных плёнках сменяется ступенчато; ширина спектральной области с низким отражением увеличивается с возрастанием числа «ступенек», при этом характер изменения ПП становится более плавным.
|