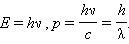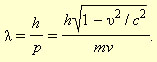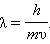Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Волновые свойства микрочастиц. Дифракция электронов
|
|
В 1923 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.
Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:
|
Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,
|
В нерелятивистском приближении (υ < < c)
|
Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то время опытного подтверждения. Но она явилась мощным революционным толчком к развитию новых представлений о природе материальных объектов. В течение нескольких лет целый ряд выдающихся физиков XX века – В. Гейзенберг, Э. Шредингер, П. Дирак, Н. Бор и другие – разработали теоретические основы новой науки, которая была названа квантовой механикой.
Дифракция электронов и нейтронов.
Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. детскому физику В. А. Фабриканту (родился в 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через устройство независимо от других (промежуток времени между двумя электронами более чем в I04 раз превышал время прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частицe в отдельности.
Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (1.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электронография и нейтронография, а также к возникновению новой отрасли науки — электронной оптики.
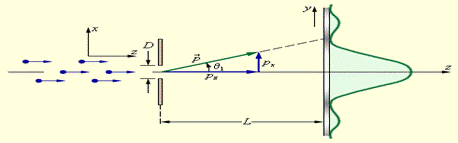
Объяснить соотношениенеопределенностей Гейзенберга на примере дифракции электронов на узкой щели. Показать, что для движущегося электрона, неопределенность координаты которого равна длине волны де Бройля, неопределенность скорости равна самой скорости.
Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ 1 этого максимума находится из условия
| D sin θ 1 = λ. |
Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение py поперечного импульса равно
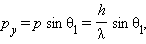
|
где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует

|
Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δ y = D. Величину Δ y называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δ py. Таким образом, величины Δ y и Δ py связаны соотношением
|
которое называется соотношением неопределенностей Гейзенберга. Величины Δ y и Δ py нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой в рассмотренном мысленном эксперименте двигался какой-то конкретный электрон после прохождения щели до фотопластинки.
Это хуевый вопрос…ниче не смог найти больше толкового
Атом
1.Закономерности в спектре излучения атома водорода.
Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.
Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
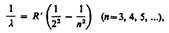 (209.1)
(209.1)
где R' = 1, 10× 107 м-1—постоянная Ридберга*. Так как v=c/A, то формула (209.1) может быть переписана для частот:
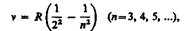 (209.2)
(209.2)
где R = R'с = 3, 29× 1015 с-1 — также постоянная Ридбeрга.
Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями л, образуют группу или серию линий, называемую серией Бальмера. С увеличением л линии серии сближаются; значение n = ¥ определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.
В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:
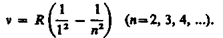
В инфракрасной области спектра были также обнаружены:
 серия Пашена
серия Пашена
серия Брэкета
серия Пфунда
серия Хэмфри
Все приведенные выше серив в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:
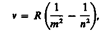 (209.3)
(209.3)
где т имеет в каждой данной серии постоянное значение, т= 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).
Исследование более сложных спектров — спектров паров щелочных металлов (на пример, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.
Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.
2. Постулаты Бора. Теория Бора для водородоподобных систем.
Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885—-1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ящерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу своей теории Бор положил два постулата.
Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию
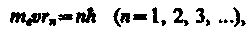
где т, — масса электрона, v — его скорость по n-й орбите радиуса rn,
ℏ = h/(2p).
Второй постулат Бора (правило частот): при переходе электрона с одной стационар ной орбиты на другую излучается (поглощается) один фотон с энергией
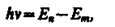
равной разности энергий соответствующих стационарных состоянии (Еn и Еm— соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При Ет< Еп происходит излучение фотона (переход атома из состояния с боль шей энергией в состояние с меньшей энергией, т. с. переход электрона с более удален ной от ядра орбиты на более близлежащую), при Ет> Еn — его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот v = (Еn – Еm)/hквантовых переходов и определяет линейчатый спектр атома.