
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переход от представления Шрёдингера к представлению Гейзенберга
|
|
Рассмотрим случай, когда 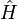 не зависит от времени. Разложим
не зависит от времени. Разложим 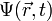 по волновым функциям стационарных состояний
по волновым функциям стационарных состояний 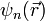 .
.
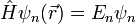 — по определению стационарных состояний.
— по определению стационарных состояний. 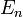 — собственная энергия
— собственная энергия
Тогда само разложение можно записать, как: 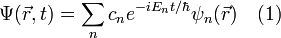
Введем унитарный оператор 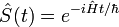
Его с ф совпадают с с ф-ми 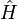 , то есть с функциями
, то есть с функциями 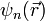 . Тогда
. Тогда 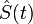 обладает следующим свойством:
обладает следующим свойством: 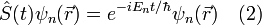
Используя этот оператор можно записать разложение 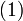 в виде:
в виде: 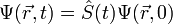
или, что то же самое: 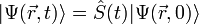 . Эта запись означает, что оператор
. Эта запись означает, что оператор 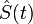 переводит состояние в начальный момент времени в состояние в произвольный момент времени.
переводит состояние в начальный момент времени в состояние в произвольный момент времени.
Теперь для того, чтобы перевести зависимость от времени с волновой функции на произвольный оператор, мы рассмотрим среднее значение некого оператора 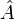 :
:
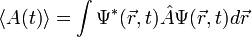 — по определению среднего значения оператора.
— по определению среднего значения оператора.
Используя оператор 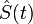 и помня, что он унитарный, можно записать среднее значение оператора
и помня, что он унитарный, можно записать среднее значение оператора 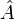 , как:
, как: 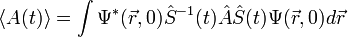
Т о мы приходим к связи произвольного оператора в представлении Гейзенберга и представлении Шрёдингера: 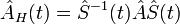 , где
, где 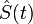 — унитарный оператор, удовлетворяющий условию
— унитарный оператор, удовлетворяющий условию  .
.
Для Гейзенберговского представления не применимо уравнение Шрёдингера. Вместо него уравнение Гейзенберга для квантовых наблюдаемых: 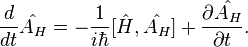
|