Метод квадратичной аппроксимации.

Квадратичная аппроксимация.

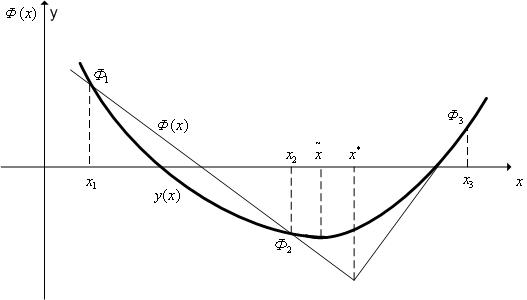
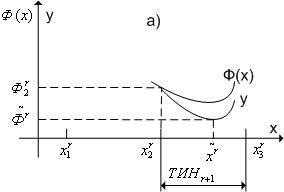
Рассмотрим квадратичную аппроксимацию (см. рис. 1). Пусть в процессе решения задачи поиска минимума функции (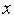) тем или иным образом получены попарно не совпадающие точки 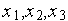, принадлежащие области допустимых значений 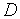(не обязательно упорядоченные слева направо!).

Рис. 1. Квадратичная аппроксимация.

Построим квадратичную функцию

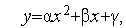
(1)

проходящую через точки , , 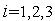где .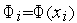

Коэффициенты 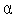, , 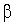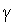функции (1) удовлетворяют системе линейных алгебраических уравнений (СЛАУ)

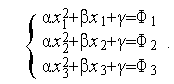
(2)

Определитель СЛАУ (2) является определителем Вандермонда, который отличен от нуля, если величины 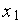, , 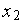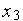попарно различны.

Таким образом, в сделанных предположениях СЛАУ (2) имеет решение и, притом единственное. Поскольку определитель СЛАУ (2) равен 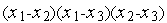, это решение имеет вид

,

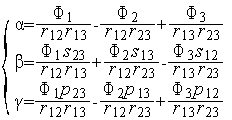где , , .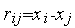

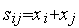Подставим найденные значения коэффициентов 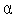, , 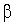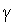в необходимое условие 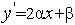=0 минимума квадратичной функции (1), получим стационарную точку этой функции

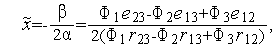
(3)

где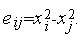

Метод квадратичной аппроксимации.

Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции (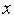), определенной в замкнутой области допустимых значений =[ , ],

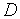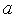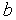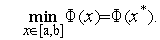
(4)

Метод квадратичной аппроксимации относится к классу методов сокращения текущего интервала неопределенности. Пусть при решении задачи (4) каким-либо методом получены три точки 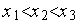, принадлежащие области допустимых значений, такие, что .

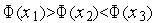Схема метода квадратичной аппроксимации:

1. Выполняем присваивания , , , , .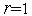

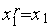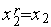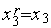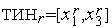2. Вычисляем значения 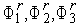функции 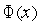в точках 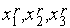, соответственно.

3. По формуле (3) вычисляем величину 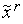и находим значение функции (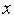) в этой точке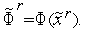

4. Находим следующие три точки:

o случай (а) - если 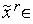[ , ], то 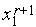= , 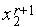= 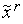, 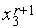= (см. рис. 2);

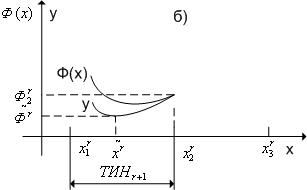
o случай (б) - если 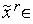[ 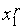, ], то 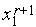= 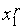, 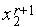= 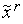, 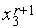= (см. рис. 3).

5. В качестве следующего текущего интервала неопределенности принимаем .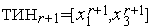

6. Если 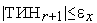, то заканчиваем вычисления. Иначе - выполняем присваивание 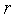= 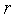+1 и переходим на п.2. Здесь 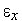– требуемая точность решения

Рис. 2. К методу квадратичной аппроксимации (случай а).

Рис. 3. К методу квадратичной аппроксимации (случай б).

В качестве приближенного значения точки минимума 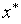с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.

Замечание. В силу условий 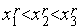, 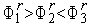точка 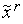всегда принадлежит текущему интервалу неопределенности ТИН _r =[ , ].

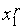Нижегородский Государственный Технический Университет

Кафедра «Вычислительные системы и технологии»

Метод квадратичной аппроксимации.

Выполнили:

Студенты гр.М12-ИВТ-3

Жарова Е.

Костюнина Н.

Н.Новгород

2013г.