Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случай неравных частот
|
|
В некоторых учебниках и пособиях говорится о том, что интерференция света возможна только для волн образованных от одного источника света путём амплитудного либо полевого деления волновых фронтов. Это утверждение является неверным. С точки зрения принципа суперпозиции интерференция существует всегда, даже когда интерферируют волны от двух разных источников света. Правильно было бы говорить о наблюдении или возможности наблюдения интерференционной картины. Последняя может быть нестационарна во времени, что приводит к замазыванию и исчезновению интерференционных полос. Рассмотрим две плоские волны с разными частотами:
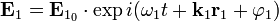 и
и 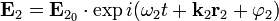
По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:
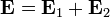
Пусть некоторый прибор, обладающий некоторым характерным временем регистрации (экспозиции), фотографирует интерференционную картину. В физической оптике интенсивностью называют усредненный по времени поток световой энергии через единичную площадку ортогональную направлению распространения волны. Время усреднения определяется временем интегрирования фотоприемника, а для устройств, работающих в режиме накопления сигнала (фотокамеры, фотопленка и т. п.), временем экспозиции. Поэтому приемники излучения оптического диапазона реагируют на среднее значение потока энергии. То есть сигнал с фотоприемника пропорционален:
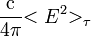
где под < > подразумевается усреднение. Во многих научно технических приложениях данное понятие обобщается на любые, в том числе и не плоские волны. Так как в большинстве случаев, например в задачах связанных с интерференцией и дифракцией света, исследуется в основном пространственное положение максимумов и минимумов и их относительная интенсивность, постоянные множители, не зависящие от пространственных координат, часто не учитываются. По этой причине часто полагают:
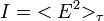
Квадрат модуля амплитуды задается соотношением:
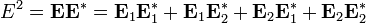
Откуда, подставляя напряженность электрического поля, получим:
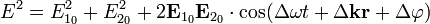 , где
, где  ,
, 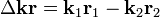 , Δ φ = φ 1 − φ 2
, Δ φ = φ 1 − φ 2
С учётом определения интенсивности можно перейти к следующиму выражению:
[1] 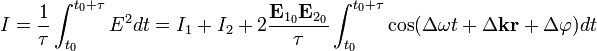 , где
, где 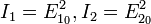 — интенсивности волн
— интенсивности волн
Взятие интеграла по времени и применение формулы разности синусов даёт следующие выражения для распределения интенсивности:
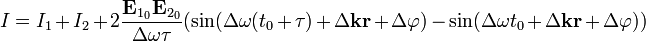
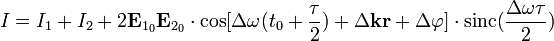
В итоговом соотношении слагаемое, содержащее тригонометрические множители, называется интерференционным членом. Оно отвечает за модуляцию интенсивности интерференционными полосами. Степень различимости полос на фоне средней интенсивности называется видностью или контрастом интерференционных полос: