
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания С. Для желающих
|
|
Вариант 1.
В1.В среднем за день во время конференции расходуется 70 пакетиков чая. Конференция длится 6 дней. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
В2. Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
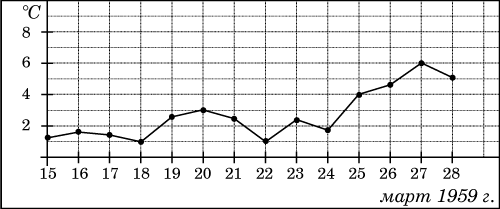
В3. На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наименьшая среднесуточная температура за указанный период. Ответ дайте в градусах Цельсия.
В4Клиент хочет арендовать автомобиль на сутки для поездки протяжённостью 500 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды.
| Автомобиль | Топливо | Расход топлива (л на 100 км) | Арендная плата (руб. за 1 сутки) |
| А | Дизельное | ||
| Б | Бензин | ||
| В | Газ |
Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива — 19 рублей за литр, бензина — 22 рублей за литр, газа — 14 рублей за литр. Сколько рублей заплатит клиент за аренду и топливо, если выберет самый дешёвый вариант?
В5. На клетчатой бумаге с размером клетки  изображён угол. Найдите его градусную величину.
изображён угол. Найдите его градусную величину.
К № 5 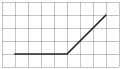 к №8
к №8 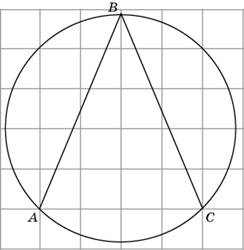
В6. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по теме " Кислоты". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме " Кислоты".
В7. Найдите корень уравнения 1) 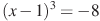
2) 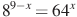 3)
3) 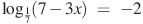
В8. Найдите угол 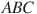 . Ответ дайте в градусах
. Ответ дайте в градусах
В9.. На рисунке изображен график 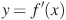 — производной функции
— производной функции 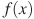 , определенной на интервале
, определенной на интервале 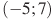 . Найдите промежутки убывания функции
. Найдите промежутки убывания функции 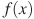 . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.

В10. Найдите квадрат расстояния между вершинами 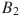 и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
К №10 
В11.Найдите значение выражения
1)  2)
2) 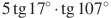
В12. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где
, где 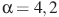 — постоянная, r — радиус аппарата в метрах,
— постоянная, r — радиус аппарата в метрах,  — плотность воды, а g — ускорение свободного падения (считайте
— плотность воды, а g — ускорение свободного падения (считайте  Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
В13. Площадь основания конуса равна 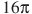 , высота — 6. Найдите площадь осевого сечения конуса.
, высота — 6. Найдите площадь осевого сечения конуса.
В14. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 63 км/ч, а вторую половину времени — со скоростью 81 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В15. 1)Найдите наименьшее значение функции  .
.
2) Найдите наибольшее значение функции 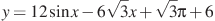 на отрезке
на отрезке 
3) Найдите точку максимума функции  .
.
Вариант 2
Задания С. Вариант 1
С1.
а)Решите уравнение 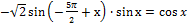
б) Найдите все корни этого уравнения, принадлежащие отрезку [ 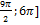
C2.В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 8. Точка L-середина ребра SC. Тангенс угла между прямыми DL и SA равен 2 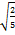 . Найдите площадь поверхности пирамиды.
. Найдите площадь поверхности пирамиды.
С3.Решите систему неравенств 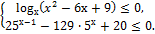
Задания С. Вариант 1
С1. а)Решите уравнение 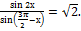
б) Найдите все корни этого уравнения, принадлежащие отрезку 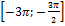 .
.
С2. В правильной четырёхугольной призме
ABCDA1B1C1D1 сторона основания равна 20, а боковое ребро АА 1=7. Точка М принадлежит ребру
A1D1 и делит его в отношении 2: 3, считая от вершины D1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D, и М.
С3. Решите систему неравенств
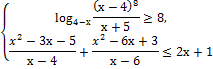
Задания С. Для желающих
С1.а) Решите уравнение 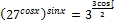 .
.
б) Найдите все корни уравнения, принадлежащие отрезку 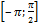 .
.
С2. В правильной четырёхугольной пирамиде MABCD с вершиной М стороны основания равны 1, а боковые рёбра равны 2. Точка N принадлежит ребру МС, причём MN: NC=2: 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки В и N параллельно прямой АС.
С3. Решите систему неравенств

С4. Окружности радиусами 2 и 9 с центрами 01 и 02 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке К, а большую – в точке М. Найдите площадь треугольника КМО1, если угол LMO2 равен 150.
С5. Найдите все значения а, при которых уравнение 8а +  имеет единственный корень.
имеет единственный корень.
С6. Дана бесконечная арифметическая прогрессия, первый член которой равен 2013. А разность равна 8. Каждый член прогрессии заменили суммой его цифр. С полученной последовательностью поступили также и действовали так до тех пор, пока не получилась последовательность однозначных чисел.
а) Найдите тысячное число получившейся последовательности.
б) Чему может равняться наибольшая сумма 1010 чисел получившейся последовательности, идущих подряд?
|