Колебания в этом случае не будут когерентными, явления интерференции наблюдаться не будет.

Результат сложения зависит от разности фаз исходных колебаний и может изменяться от при до при 0

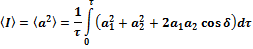
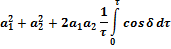
Если остается неизменной в течении времени наблюдения, то, следовательно

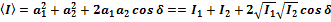
Волны, возбуждающие колебания, разность фаз которых остается постоянной во времени, называются когерентными волнами.

При беспорядочном же изменении разности фаз в течении времени, которое происходит в результате обрыва и возобновления колебаний

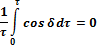
(значение 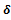многократно пробегает значения от 0 до 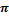). И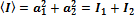

Колебания в этом случае не будут когерентными, явления интерференции наблюдаться не будет.

Интерференция света — (от лат. inter - взаимно, между собой и ferio - ударяю, поражаю), сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны.

Интерференция света — перераспределение интенсивности света в результате наложения нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Предположим, что две монохроматические световые волны (лямбда константна), накладываюсь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления: х₁ = А₁cos( t +  ₁) и x₂ = A₂cos( t +  ₂).Под х понимают напряженность электрического Еили магнитного Нполей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях. Напряженности электрического и магнитного полей подчиняются принципу суперпозиции (результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.). Амплитуда результирующего колебания в данной точке A² = A²_l + A²₂ + 2A₁A₂ cos( ₂ -  ₁). Так как волны когерентны, то cos( ₂ - ₁) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (1~А²)

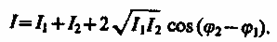(172.1)

В точках пространства, где > 0, интенсивность I > I₁ + I₂, где < 0, интенсивность I < I₁ + I₂. Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности. Это явление называется интерференцией света.

Для некогерентных волн разность 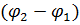непрерывно изменяется, поэтому среднее во времени значение равно нулю, и интенсивность результирующей волны всюду одинакова и при I₁ = I₂равна 2I₁(для когерентных волн при данном условии в максимумах I = 4I₁ в минимумах I = 0).

Как можно создать условия, необходимые для возникновения интерференции световых волн? Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.

Пусть разделение на две когерентные волны происходит в определенной точке О. До точки М, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления n₁ прошла путь s₁, вторая - в среде с показателем преломления n₂ - путь s₂. Если в точке О фаза колебаний равна  t, то в точке М первая волна возбудит колебание А₁cos (t – s₁/v₁), вторая волна - колебание А₂cos (t – s₂/v₂), где v₁ = c/n₁, v₂ = c/n₂- соответственно фазовая скорость первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна

м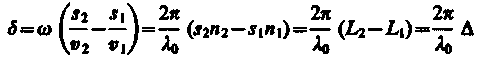

(учли, что  /с = 2 v/с = 2  ₀ где  ₀ - длина волны в вакууме). Произведение геометрической длины sпути световой волны в данной среде на показатель nпреломления этой среды называется оптической длиной пути L, a  = L₂ – L₁ - разность оптических длин проходимых волнами путей - называется оптической разностью хода. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей

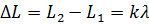• — условие максимума;
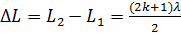— условие минимума, где k=0, 1, 2… и 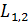— оптическая длина пути первого и второго луча, соответственно.

1. Метод Юнга. Источником света служит ярко освещенная щель S(рис. 245), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллельные щели S. Таким образом, щели S₁ и S₂играют роль когерентных источников.

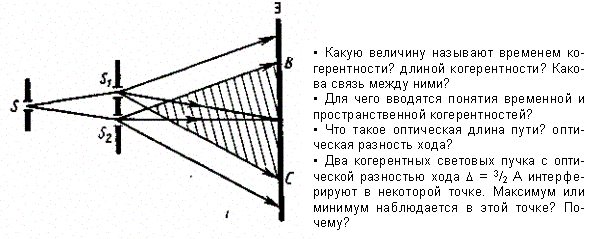
Рис. 245

Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S₁ и S₂. Как уже указывалось (см. § 171), Т. Юнгу принадлежит первое наблюдение явления интерференции.

2. Зеркала Френеля. Свет от источника S (рис.246) падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол  мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S₁ и S₂(угловое расстояние между которыми равно 2)лежат на одной и той же окружности радиуса r с центром в О(точка соприкосновения зеркал).

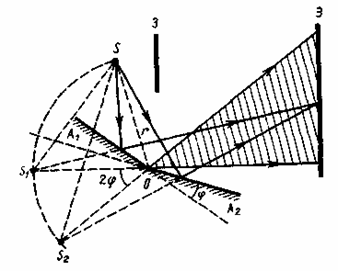
Рис. 246

Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S₁ и S₂, являющихся мнимыми изображениями S в зеркалах.

Мнимые источники S₁ и S₂ взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2. Интерференционная картина наблюдается на экране (Э), защищенном от прямого попадания света заслонкой (3).

3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.

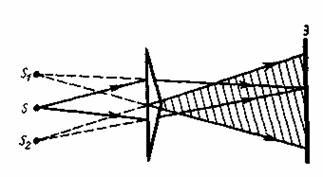
Рис. 247

Расчет ин терференционной картины от двух источников. Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 248).

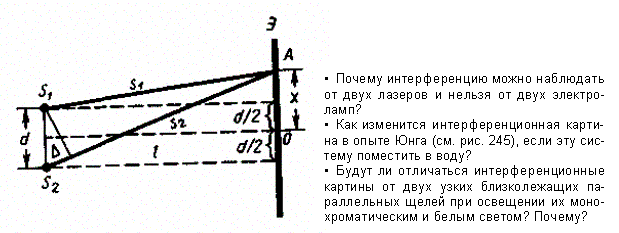
Рис. 248

Щели S₁ и S₂находятся на расстоянии dдруг от друга и являются когерентными (реальными или мнимыми изображениями источника Sв какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l ≫ d. Начало отсчета выбрано в точке О, симметричной относительно щелей.

Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода  = s₂ – s₁ Из рисунка имеем:

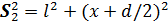
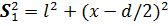
Откуда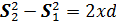

Или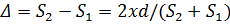

Из условия 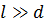следует, что 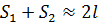, поэтому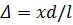

Подставив полученное выражение в формулы

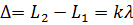
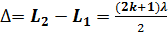
Получим, что максимумы интенсивности будут наблюдаться в случае, если

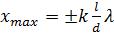, (k=0, 1, 2, 3…),

а минимумы - в случае, если

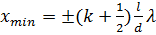, (k=0, 1, 2, 3…),

Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно

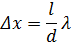
 х не зависит от порядка интерференции (величины m) и является постоянной для данных l, d и  ₀. Согласно формуле 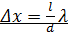,  x обратно пропорционально d;

следовательно, при большом расстоянии между источниками, например при d  l, отдельные полосы становятся неразличимыми.Для видимого света  ₀  10^-7м, поэтому четкая, доступная для визуального наблюдения интерференционная картина имеет место при l≫ d (это условие и принималось при расчете). По измеренным значениямl, d в  х, используя 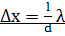, можно экспериментально определить длину волны света. Из выражений (173.2) и (173.3) следует, таким образом, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m = 0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д.

Описанная картина справедлива лишь при освещении монохроматическим светом (λ ₀ = const). Если использовать белый свет, представляющий собой непрерывный набор длин волн от 0, 39 мкм до 0, 75 мкм, то интерференционные максимумы для каждой длины волны будут, согласно описанной выше формуле, смещены друг относительно друга и иметь вид радужных полос. Только для m = 0максимумы всех длин волн совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т. д. (ближе к белой полосе будут находиться зоны фиолетового цвета, дальше - зоны красного цвета).

при отражении от оптически боле плотных сред фаза меняется на пи.