Производственные задачи

Для изготовления двух видов продукции 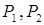используют три вида сырья: 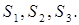Запасы сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая

от реализации единицы продукции приведены в таблице 1.1. Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.

Таблица 1.1.

Вид сырья	Запасы сырья	Кол-во единиц сырья, идущих на изготовление единицы продукции
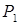
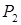
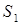
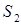
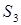
Прибыль от единицы продукции, руб.

Обозначим через 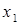количество единиц продукции 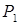, а через 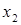количество единиц продукции 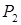. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

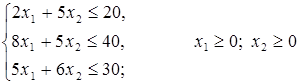(1.1)

которая показывает, что количество сырья, необходимое на изготовление продукции, не может превысить имеющихся запасов. Если продукция 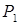не выпускается, то 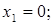в противном случае

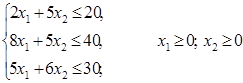
То же самое и для продукции 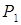. Таким образом, на неизвестные 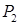и 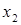должно быть наложено ограничение не отрицательности: .

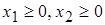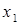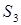Конечную цель решаемой задачи - получение максимальной прибыли при реализации продукции - выразим как функцию двух переменных и . Реализация 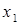единиц продукции вида 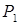и 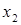единиц продукции вида 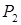дает соответственно 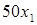и 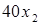руб. прибыли, суммарная прибыль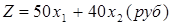

Условиями не оговорена неделимость единицы продукции, поэтому 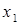и 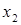могут быть и дробными числами. Необходимо найти такие неотрицательные значения 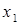и 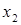, которые удовлетворяли бы системе ограничений и при которых функция 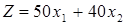имела бы максимальное значение.