
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон нормального распределения. Проверка нормальности распределения
|
|
Известный немецкий математик, астроном, физик и геодезист Карл Фридрих Гаусс в 1809 г. доказал, что большинство случайных величин подчиняется закону, который впоследствии был назван – закон нормального распределения.
Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественно-научных исследованиях и казалось «нормой» всякого массового случайного проявления признаков. Если представить этот закон графически, то он будет представлять собой так называемую колоколообразную кривую (см. рис. 3.1).
График нормального распределения определяется средним арифметическим числом и стандартным отклонением. Плотность нормального распределения симметрична относительно среднего.
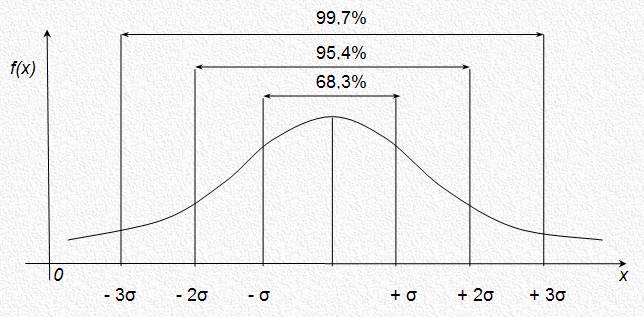
Рис 3.1 График нормального распределения
Если при обработке полученных данных мы получаем графики с характерным уклоном вправо или влево (см. рис. 3.2), то мы имеем дело с асимметричным распределением.

Рис.3.2 График асимметричного распределения
Терминасимметрия (коэффициент асимметрии, выборочный коэффициент скошенности) впервые был введен Пирсоном, 1895.
Асимметрией называют меру отклонения эмпирического распределения частот от симметричного распределения относительно максимальной ординаты.
Для симметричного распределения показатель асимметрии равен нулю. Отрицательный показатель асимметрии означает скошенность кривой распределения вправо, это когда количество значений больших среднего, превышает количество значений – меньших. Положительный показатель асимметрии означает скошенность кривой распределения влево от теоретической симметричной кривой распределения, это в том случае, когда количество значений меньших среднего, превышает количество значений больших среднего (см. рис. 3.3).
Если мы получаем графики «вытянутые» или «приплюснутые» (см. рис. 3.3), то мы имеем дело с эксцессом.
Терминэксцесс (коэффициент эксцесса) впервые был введен Пирсоном, 1905.
Степень отклонения эмпирической кривой распределения от теоретической кривой нормального распределения количественно выражается показателем эксцесса (выборочным коэффициентом островершинности.
Нормальное распределение имеет эксцесс равный нулю.
Положительный эксцесс соответствует островершинной кривой эмпирического распределения (заостренной), отрицательный – туповершинной (пологой) по сравнению с нормальной кривой.
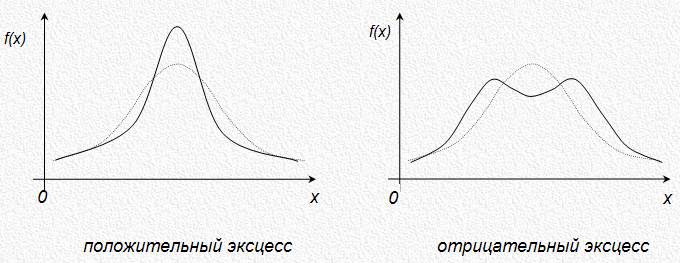
Рис.3.3 Эксцесс
Преобладание в распределении значений близких к среднему, способствует возникновению положительного эксцесса. Преобладание значений близких к крайним значениям (одновременно низких и высоких), способствует возникновению отрицательного эксцесса.
Проверка нормальности распределения необходима в случае применения параметрических методов. Во всех остальных случаях нет необходимости проверять нормальность распределения полученных эмпирических данных.
Разработан ряд процедур проверки нормальности распределения результатов наблюдений, среди них можно выделить следующие:
Для оценки асимметрии применим формулу 3.7.
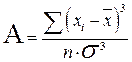 (3.7)
(3.7)
где: σ – (сигма) стандартное отклонение находится по формуле 3.8.
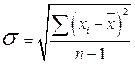 (3.8)
(3.8)
где: n – количество измеренных признаков;
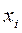 – каждое значение признака;
– каждое значение признака;
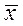 – среднее арифметическое.
– среднее арифметическое.
В идеале для симметричных распределений показатель оценки асимметрии равняется нулю.
Показатель оценки асимметрии сравниваем с критическими значениями, полученными с помощью формулы 3.9 (Плохинского Н.А.) или формулы 2.17 (Пустыльника Е.И.).
Формула Плохинского Н.А.:
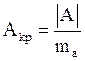 (3.9)
(3.9)
где: 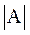 - показатель оценки асимметрии в модуле;
- показатель оценки асимметрии в модуле;
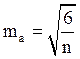 - ошибка репрезентативности (3.10)
- ошибка репрезентативности (3.10)
n – количество наблюдений.
Если показатель оценки асимметрии не превышают свою ошибку репрезентативности в три раза, то это свидетельствует о том, что полученные данные имеют вид нормального распределения, т.е. если А кр 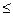 3 то полученные данные распределены по нормальному закону распределения.
3 то полученные данные распределены по нормальному закону распределения.
Формула Пустыльника Е.И.:
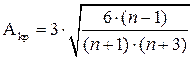 (3.11)
(3.11)
где: n – количество наблюдений.
Если А эмп 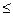 А кр, то полученные данные распределены по нормальному закону распределения.
А кр, то полученные данные распределены по нормальному закону распределения.
Для оценки эксцесса применим формулу 3.12.
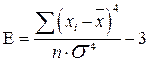 (3.12)
(3.12)
В идеале для нормального распределения показатель оценки эксцесса равняется нулю.
Показатель оценки эксцесса сравниваем с критическими значениями, полученными с помощью формул 3.13 или 3.15 (Плохинского Н.А., Пустыльника Е.И.):
Формула Плохинского Н.А.:
 (2.13)
(2.13)
где: 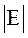 - показатель оценки эксцесса в модуле;
- показатель оценки эксцесса в модуле;
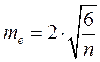 -ошибка репрезентативности (3.14)
-ошибка репрезентативности (3.14)
n – количество наблюдений.
Если показатель оценки эксцесса не превышает свою ошибку репрезентативности в три раза, то это свидетельствует о том, что полученные данные имеют вид нормального распределения.
Формула Пустыльника Е.И.:
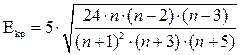 (3.15)
(3.15)
где: n – количество наблюдений.
Если E эмп 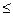 E кр, то полученные данные распределены по нормальному закону распределения.
E кр, то полученные данные распределены по нормальному закону распределения.
Более точную информацию о форме распределения можно получить с помощью одного из методов: критерия Шеффе, критерия Ливина, критерия Бартлетта, критерия Колмогорова-Смирнова, W критерия Шапиро-Уилка и т.д.