
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие скорости реакции
|
|
К сожалению, многие учебники химии построены не вполне логично, в частности, одно и то же слово может использоваться в разных смыслах, поэтому предлагается очень внимательно ознакомиться с разными определениями скорости и не путать их.
(а) Скорость реакции (на мИкроскопическом уровне) – это число её элементарных актов в единицу времени в единице объёма (для гомогенных реакций) или на единице площади контакта фаз (для гетерогенных)1.
(б) Скорость реакции (на мАкроскопическом уровне) – это количество вещества, вступающего в реакцию или образующегося при реакции в единицу времени в единице объёма (для гомогенных реакций) или на единице площади контакта фаз (для гетерогенных) [1]. (Из учебника Глинки [1, 2]).
(в) Скорость гомогенной реакции (на мАкроскопическом уровне) – это изменение концентрации исходного вещества или продукта в единицу времени. (Тоже из учебника Глинки).
Определение (а) – самое строгое, но им очень трудно пользоваться, т.к. очень трудно считать элементарные акты. Поэтому на практике скорость обычно определяют через мАкроскопические параметры – измеримые на опыте количества или концентрации веществ, как в определениях (б) и (в).
Обычно в элементарном акте рождаются и гибнут одна или две частицы, поэтому скорость в смысле (а) получается умножением скорости в смысле (б) на NA или на NA/2 (NA – число Авогадро). Таким образом, скорости (а) и (б), хотя и разные, но связаны однозначно, поэтому закономерности, выведенные для одной, должны быть однозначно справедливы и для другой. Но заметьте: здесь неявно подразумевается, что данные частицы рождаются или гибнут в результате только одной реакции, а так бывает далеко не всегда. Обычно протекает одновременно две или несколько разных реакций.
Разные реакции, в которых одно и то же вещество расходуется или образуется, называются параллельными. Например, если в кислоте растворяется смесь оксида и карбоната кальция, то кислота расходуется в двух независимых процессах: СаО+2Н+→ Са2++Н2О и СаСО3+2Н+→ Са2++Н2О+СО2. Скорость расхода ионов водорода – это сумма скоростей этих реакций.
Если продукт одной реакции является исходным веществом для другой, такие реакции называются последовательными. Например, С2Н2+Н2→ С2Н4, С2Н4+Н2→ С2Н6. В этом случае скорость образования этилена С2Н4 есть разность скоростей первой и второй реакции.
Кроме того, почти все реакции обратимы, т.е. продукты реакции имеют шанс при новых столкновениях опять превратиться в исходные вещества, например, Н2+I2 ← → 2HI. Здесь тоже скорость расходования водорода и образования иодоводорода есть разность скоростей прямой и обратной реакций. Позже мы будем изучать химическое равновесие, когда скорости прямой и обратной реакций становятся одинаковыми [1, § 63]. При этом сколько вещества образуется, столько и расходуется, поэтому количество вещества не меняется, и скорость в смысле (б) равна нулю. Следовательно, когда говорят, что идут с одинаковыми скоростями прямая и обратная реакции, то подразумевают скорость в смысле (а), а не в смысле (б), как указано в одном из предыдущих параграфов того же учебника.
Таким образом, определение (б) эквивалентно определению (а) лишь при условии, что реакция необратима и никаких других реакций с участием данных веществ не происходит. Об этом часто забывают.
Эквивалентны ли определения (б) и (в) в случае гомогенной реакции? Концентрация – это количество вещества в единице объёма. Поэтому изменение количества вещества в единице объёма – это и есть изменение концентрации. Не так ли? Но в промышленных реакторах непрерывного действия все время вводятся реагенты и выводятся продукты, так что концентрации в определённой точке могут быть постоянны, хотя реакция идет. Скорость в смысле (б) может быть очень большой, а скорость (в) равна нулю.
Кроме того, все три определения предполагают, что объём системы не меняется. Если, например, газовая реакция идет с расширением, то и число элементарных актов, и количества веществ в единице объёма будут изменяться не только от свойств самой реакции по законам химической кинетики, но и от изменения объёма.
Мы будем далее пользоваться традиционным определением: скорость гомогенной реакции – это изменение концентрации какого-то из реагентов или продуктов в единицу времени, но помня, что это величина верно характеризует данную конкретную реакцию только при следующих условиях:
– реакция необратима;
– исходные вещества и продукты не участвуют ни в каких других реакциях;
– объём системы постоянен;
– никакие вещества в систему не добавляются и из неё не выводятся.
Два последних условия легко обеспечить, а два первых не всегда очевидны.
Изменение концентрации исходного вещества отрицательно, поэтому, чтобы получить положительную скорость, перед ним нужно поставить минус, а если измерять по продуктам – то плюс.
vгом. = ±DС/Dt.
Попутно договоримся о символах. Чтобы не путать скорость с объёмом, пусть скорость будет малой v, а объём – заглавной V. Температура по Цельсию – t, время – t (греческая тау), количество вещества – n, концентрация – С. Другое обозначение концентрации – формула вещества в квадратных скобках: Н+ – ион, [Н+] – цифра, его концентрация в моль/л. Обычно в квадратных скобках пишут концентрацию реальных частиц, например, ионов, образовавшихся при распаде электролита, а буквой С обозначают концентрацию вещества, введённого в раствор, независимо от того, что с ним там произошло. Например, С(H2SO4) = 0, 1 моль/л означает, что в литр раствора введёно 0, 1 моля серной кислоты, хотя там уже нет молекул H2SO4, а есть ионы Н+ и SO42- в концентрациях 0, 2 и 0, 1 моль/л соответственно. Символ D – греческая дельта – обозначает изменение величины: DС=С2–С1, Dt=t2–t1.
Выше определена средняя скорость, а реально она все время меняется, поэтому для определения мгновенной скорости, как и в механике, нужно взять производную концентрации по времени:
vгом. = ± dC/dt.
В гетерогенном процессе концентрация часто не имеет смысла, поэтому нужно контролировать изменение количества вещества n в единицу времени, отнесенное к площади контакта S или к массе смеси m, или к исходному количеству вещества:
vгет. = ± dn/(Sdt) или v’гет.= ± dn/(m0dt) или v’’гет.= ± dn/(n0dt).
Эти определения совершенно разные. Можно пользоваться любым (если мы умеем определять S), но не нужно забывать, каким определением мы пользуемся. Например, в одном из школьных учебников было дано первое определение, а на следующей странице говорилось, что скорость пропорциональна S. Это нелепость. Ведь первая формула содержит S в знаменателе. Она для того и введена, чтобы избавиться от влияния площади. Если, например, у нас кусок мрамора Сa СО3 растворяется в кислоте, и мы добавим второй такой же кусок, то площадь увеличится вдвое, количество СО2 в единицу времени увеличится вдвое, а v – их отношение – не изменится. Авторы учебника пишут первое определение, а фактически подразумевают второе или третье. Тогда, действительно, скорость пропорциональна S: если мы ту же массу мрамора измельчим, площадь контакта увеличится, и количество СО2 в единицу времени увеличится. Поскольку мы обычно не можем измерить S, будем пользоваться вторым или третьим определением.
1.3. Контрольные вопросы и задания (подготовиться к обсуждению на семинаре)
(а) Дайте определения скорости гомогенной реакции на микроскопическом и макроскопическом уровне и объясните границы их применимости.
(б) Дайте определения скорости гетерогенной реакции на микроскопическом и макроскопическом уровне и объясните границы их применимости.
(в) Что такое параллельные, последовательные, обратимые реакции?
(г) Зависит ли скорость гетерогенной реакции от площади контакта фаз? Если да, то как?
2. Зависимость скорости гомогенной реакции
от концентраций реагентов
2.1. Краткая теория [1, § 58; 2, § 6.2.3]
Основное уравнение гомогенной кинетики – закон действующих масс, ЗДМ (хотя реально подставляются не массы, а молярные концентрации):
Скорость гомогенной реакции, протекающей в одну стадию, пропорциональна концентрациям реагентов, взятым в степенях с показателями, равными соответствующим коэффициентам в уравнении реакции. Здесь идёт речь об истинной, т.е. микроскопической, скорости.
Если реакция выражается уравнением
aA + rR → mM
(большие буквы – некие абстрактные частицы – молекулы или ионы, а маленькие – коэффициенты), то
v = K•[A]a•[R]r,
где коэффициент пропорциональности K – константа скорости данной реакции. Смысл закона в том, что скорость реакции пропорциональна частоте столкновений частиц, а эта частота пропорциональна концентрации каждой из частиц, будь они одинаковыми или разными. Если реакция типа A+R→ T, то v = K•[A]•[R], а если реакция типа A+A→ T, то v = K•[A]2.
Если в реакции участвует газ, то принято вместо концентрации писать в кинетическом уравнении его парциальное давление. Согласно уравнению Менделеева-Клапейрона, оно пропорционально концентрации: p = nRT/V = СRT, т.к. n/V = C.
Уравнение ЗДМ не имеет смысла, если a + r > 3, потому что столкновение более трех частиц в одной точке практически невероятно. Число частиц (молекул, ионов, радикалов), участвующих в элементарном акте химической реакции, называется молекулярностью реакции. Поэтому различают мономолекулярные, бимолекулярные и тримолекулярные реакции.
При составлении химических уравнений очень часто сумма коэффициентов в левой части получается больше 3. Это однозначно показывает, что реакция является сложной, многостадийной, а мы записали лишь сумму нескольких стадий на основе законов сохранения. Такое уравнение («что взяли – что получили») нужно для расчёта соотношений между количествами расходующихся и образующихся веществ, а также для рассмотрения химического равновесия (гл. 7-11). Но оно не показывает механизм реакции; уравнения отдельных элементарных актов остаются неизвестными. При этом наблюдаемая (макроскопическая) скорость реакции зависит от скоростей отдельных стадий сложным образом. Довольно очевидно, что в цепочке последовательных реакций скорость получения конечного продукта будет ограничена скоростью самой медленной стадии. Но не обязательно при этом наблюдаемая скорость будет точно подчиняться ЗДМ для этой медленной стадии, т.к. остальные стадии тоже влияют.
Зависимость макроскопической скорости сложной реакции от концентраций реагентов обычно подчиняется ЗДМ, но при этом показатели степени уже не равны коэффициентам суммарного уравнения и даже коэффициентам самой медленной стадии; они могут получиться даже дробными. Порядком реакции по данному реагенту называется показатель степени, в которую нужно возвести концентрацию данного реагента, чтобы уравнение ЗДМ правильно описывало экспериментальную зависимость скорости от концентрации. Суммарный порядок – это сумма порядков по всем реагентам. Порядок и молекулярность совпадают лишь в простейших случаях, но экспериментальное изучение порядков реакций – один из путей к пониманию их истинных механизмов.
Разумеется, если сумма коэффициентов в левой части уравнения реакции не превышает 3, это ещё не означает автоматически, что реакция одностадийная. Она всё равно может быть сложной, и без экспериментальной проверки вопрос не решается.
2.2. Контрольные вопросы и задания (нужны письменные ответы и решения в тетради для домашних заданий)
(а) На основе уравнения ЗДМ объясните физический смысл константы скорости.
(б) Зависит ли константа скорости от концентраций реагентов? от их природы? от способа выражения концентрации? от температуры?
(в) Что такое молекулярность и порядок реакции, в каких случаях они совпадают?
(г) В термохимии принято записывать уравнения реакций образования веществ в расчёте на один моль продукта. Например: 1/2 Н2 + 1/2 I2 → HI, а не Н2 + I2 → 2HI. Если реакция одностадийная, то любое ли из этих уравнений годится для описания кинетики?
(д) Как изменится скорость газовой реакции 2A+R→ 2M, если объём сосуда уменьшить в три раза? Какое предположение нужно сделать, чтобы задача имела однозначное решение?
(е) Задачи 326, 328 [3] или 329, 331 [4].
2.3. Лабораторная работа: определение порядка реакции тиосульфата натрия с кислотой в растворе
2.3.1. Постановка задачи
Реакцию можно выразить следующими уравнениями
(а) Na2S2O3 + H2SO4 → S↓ + H2SO3 + Na2SO4
(б) Na2S2O3 + 2HCl → S↓ + H2SO3 + 2 NaCl
(в) S2O32– + 2H+ → S↓ + H2SO3
(г) S2O32– + 2H+ → S↓ + H2O + SO2
(д) S2O32– → S↓ + SO32–
Вам предлагается проделать опыты, определить порядок реакции по каждому из реагентов и выбрать наиболее правильный вариант уравнения на основе результатов опытов и известных фактов, что Na2S2O3, H2SO4, HCl, Na2SO4 и NaCl – сильные электролиты, т.е. в растворе практически полностью распадаются на ионы, а H2SO3 – электролит средней силы, т.е. тоже распадается, но в крепких растворах не полностью.
Признаком протекания реакции является образование твёрдой фазы серы, которое фиксируется по появлению помутнения. Конечно, правильнее измерять мгновенные скорости реакции в разные моменты времени, но это требует сложного оборудования и квалификации, а в данной работе мы будем измерять среднюю скорость реакции за время τ от момента смешивания реагентов до первых признаков появления серы.
Для появления заметного помутнения требуется накопить в растворе некоторую неизвестную, но постоянную концентрацию серы С. Тогда средняя скорость реакции – это С/τ, а поскольку С считается константой, то в качестве условной меры скорости можно взять величину 1/τ.
Скорость реакции, вообще говоря, зависит от концентрации каждого реагента, температуры, растворителя, наличия катализаторов и т.д. Поэтому, чтобы наблюдать влияние одного фактора, надо поддерживать все остальные постоянными.
Запишите комнатную температуру и концентрации выданных растворов. Берите каждый реагент всегда из одной и той же банки и отмеряйте его объём одним и тем же мерным цилиндром (своим для каждого реагента!), чтобы исключить влияние возможных различий в концентрациях и в градуировке цилиндров. Если раствора в банке недостаточно, попросите добавки сразу, до начала опытов.
2.3.2. Зависимость скорости реакции от концентрации ионов водорода
Заготовьте в тетради заранее таблицу для записи исходных данных и результатов опытов. Сейчас в неё внесены некоторые предполагаемые объёмы растворов, но эти цифры писать не надо, они даны лишь для примера, а на практике может, например, оказаться, что такие объёмы неудобно смешивать, и надо взять другие – это зависит от объёма пробирок или стаканов, используемых для смешивания. Главное, чтобы концентрация тиосульфата была везде одинаковой, а концентрация кислоты менялась в широких пределах. Чтобы при этом поддерживался одинаковый объём реакционной смеси, нужно заранее добавить расчётный объём воды к одному из реагентов (или часть к одному, часть к другому в первых двух опытах). Этим условиям удовлетворяют строки 1-4, а в остальных строках – наоборот, постоянная концентрация кислоты и переменная – тиосульфата для п. 2.3.3.
Зависимость скорости реакции от концентраций реагентов
(укажите комнатную температуру)
| № | Исходные объёмы растворов, мл | Исходные концентрации, моль/л | τ, с | 1/τ, с–1 | |||
| Na2S2O3 | кислота | вода | [S2O32–] | [H+] | |||
| 0, 125 | 0, 05 | ||||||
| 0, 125 | 0, 25 | ||||||
| 0, 125 | 0, 50 | ||||||
| 0, 125 | 0, 75 | ||||||
| 0, 25 | 0, 25 | ||||||
| 0, 375 | 0, 25 |
Воду для разбавления нужно брать не водопроводную, а дистиллированную. И не только из-за наличия растворённых солей. В данном случае важнее то, что водопроводная вода может иметь температуру, отличную от комнатной, и опыты получатся не при одинаковой температуре. По той же причине не берите пробирки за нижнюю часть, контактирующую с раствором, чтобы не нагревать растворы теплом рук.
Концентрации реагентов в момент смешивания нужно вычислить из очевидного условия, что исходное количество вещества n не меняется от разбавления: n = C1•V1 = C2•V2, где C1 – концентрация раствора в банке, V1 – объём взятого из банки раствора, C2 – исходная концентрация в момент смешивания, V2 – общий объём раствора. Он, очевидно, равен сумме смешанных объёмов (в таблице – 20 мл). Отсюда C2 = C1•V1/V2.
Сейчас в таблице записаны в качестве примера цифры, вычисленные при условии, что концентрации растворов в банках [S2O32–] = 0, 5 моль/л, [Н+] = 1 моль/л. Разумеется, в лаборатории могут быть другие растворы, поэтому эти цифры заносить в свою тетрадь заранее не надо.
Имея секундомер, опыты может делать один студент, но обычно удобнее вдвоём. Один включает-выключает секундомер или следит за секундной стрелкой часов и записывает результаты, другой быстро и тщательно смешивает растворы и отмечает момент самого легкого помутнения. Его лучше видно на чёрном фоне. Разумеется, если оба реагента отмерять одним цилиндром, то помутнение начнётся уже в цилиндре! Посуду рекомендуется мыть сразу после опыта, пока на стенки не осел толстый налёт серы.
Обратите внимание на стиль оформления таблицы. Единицы измерения нужно указывать обязательно, но не у каждой цифры, а в заголовках колонок. Соблюдайте правила приближённых вычислений: в результате нужно указывать столько значащих цифр, сколько их было в сомножителе (или делителе или делимом) с наименьшим числом значащих цифр (а в промежуточных вычислениях можно оставлять одну дополнительную цифру). Если, например, τ = 21 с, то 1/τ – не 0, 05, и не 0, 047619, а 0, 048 с–1. Но концентрации выданных растворов везде одни и те же, поэтому их можно считать точными.
Проделав все опыты, постройте в тетради по клеточкам или на миллиметровой бумаге график зависимости 1/τ от [H+]. Оптимальная форма – квадрат со стороной около 10 см. Не забывайте, что начало координат – тоже экспериментальная точка: если кислоту не добавлять, то осадок не образуется (точнее, образуется крайне медленно!). По форме графика оцените порядок реакции: вспомните, что функция нулевого порядка – это константа, её график – прямая, параллельная оси абсцисс; график первого порядка – прямая, проходящая через начало координат; графики второго и третьего порядка – параболы, тоже проходящие через начало координат, т.к. свободного члена в ЗДМ нет. Чтобы отличить квадратичную параболу от кубической, можно построить зависимость не от концентрации, а от её квадрата, или использовать логарифмирование, но в данном опыте в этом нет нужды.
Разумеется, всегда есть случайные погрешности измерений, особенно существенные, когда время помутнения маленькое, поэтому не следует ожидать, что точки будут идеально следовать прямой или параболе. Небольшие отклонения неизбежны, и всё же вывод обычно получается достаточно определённый.
2.3.3. Зависимость скорости реакции от концентрации ионов тиосульфата
Опыты выполняются аналогично, с той разницей, что теперь постоянна концентрация кислоты, а переменна концентрация тиосульфата. В таблице этому соответствуют строки 2, 5 и 6. Таким образом, делаются два новых опыта 5 и 6, к ним добавляются ранее полученные данные опыта 2, и на графике зависимости 1/τ от концентрации тиосульфата получается четыре экспериментальные точки (с учётом начала координат).
Аналогично определите по графику порядок реакции по тиосульфату. Сделайте вывод: какое из уравнений (а) – (д) лучше всего описывает наблюдаемую кинетику реакции.
3. Зависимость скорости реакции от температуры
3.1. Краткая теория [1, § 59; 2, § 6.2.2, 6.2.5]
В старом учебнике Глинки [1, § 59] вопрос хорошо изложен на качественном уровне, но не хватает строго количественного описания влияния температуры на скорость реакции и способа определения энергии активации. Используемый там «температурный коэффициент скорости реакции» удобен для устного счёта, но не имеет физического смысла. В эпоху компьютеров следует пользоваться более строгим, физически обоснованным уравнением Аррениуса:
K = A•exp[–Ea/(kT)] или K = A•exp[–Ea’/(RT)].
Здесь К – константа скорости реакции, Ea – её энергия активации (в расчёте на один элементарный акт), Ea’ – то же, в расчёте на моль элементарных актов, k – постоянная Больцмана, R – универсальная газовая постоянная (R = k • NA), T – абсолютная температура, А – предэкспоненциальный (частотный) множитель. Если используется микроскопическое понятие скорости гомогенной реакции (через число элементарных актов), то К – это число элементарных актов в единицу времени в единице объёма при единичных концентрациях всех реагентов, А – это частота столкновений участников реакции в ориентации, необходимой для реакции, в единице объёма при единичных концентрациях всех реагентов, а экспонента выражает, на основе распределения Больцмана, долю частиц, обладающих энергией равной или большей, чем энергия активации. При использовании макроскопического определения скорости, через изменение количества вещества, нужно поделить К и А на число Авогадро. В величине А можно выделить два сомножителя: частотный и геометрический факторы. Первый даёт частоту столкновений, второй – геометрический – вероятность благоприятной ориентации.
Таким образом, «предэкспонента» А характеризует частоту столкновений нужных частиц в нужной ориентации при единичных концентрациях, а экспонента – вероятность того, что столкновение будет активным, т.е. с достаточной энергией для осуществления реакции. Первый сомножитель всегда очень большой, а скорость реакции ограничивается высокой энергией активации, низкой температурой и, соответственно, малой величиной экспоненты.
Физический смысл энергии активации на микроскопическом уровне объяснён в учебниках [1, 2]. Эта энергия расходуется на разрыв или ослабление межатомных связей в исходных молекулах, ионах или немолекулярных телах, чтобы они могли превратиться в другие частицы (возможно, даже с выделением энергии большей, чем затраченная). Но мы в лабораторной работе (см. ниже) будем наблюдать не сами активные столкновения, а мАкроскопический результат – изменение концентрации вещества. При этом энергия активации, определяемая из наклона аррениусова графика, есть мАкроскопическая характеристика, учитывающая все эффекты температуры, например, кинетику и смещение равновесия промежуточных реакций, изменение вязкости раствора, его тепловое расширение и т.п.
Таким образом, макроскопическая энергия активации – это всего лишь эмпирически подобранный параметр, который надо подставить в уравнение Аррениуса, чтобы оно правильно описывало наблюдаемую зависимость скорости реакции от температуры. МАкро- и мИкроскопическая энергии активации совпадают не всегда (так же, как порядок и молекулярность реакции).
Следует добавить, что уравнение Аррениуса справедливо не только в химической кинетике, но и для процессов диффузии и ионной проводимости в кристаллах, и для электропроводности полупроводников, хотя величины К, А и Еа там, конечно, имеют иной физический смысл.
3.2. Контрольные вопросы и задания (нужны письменные ответы в тетради для домашних заданий!)
(а) Зависят ли энергия активации и предэкспоненциальный множитель от природы реагентов? от их концентраций? от температуры? от присутствия посторонних веществ?
(б) Можно ли объяснить ускорение реакции при нагревании увеличением частоты столкновений в результате возрастания средней скорости частиц? Для ответа на вопрос найдите, во сколько раз возрастет средняя кинетическая энергия частиц и их средняя скорость при нагревании на 10 К от комнатной температуры (298 К → 308 К).
(в) Оцените среднюю кинетическую энергию частиц при комнатной температуре (например, по формуле для двухатомного идеального газа) и сделайте вывод: может ли на опыте наблюдаться энергия активации 3 кДж/моль? 50 кДж/моль? 1000 кДж/моль?
(г) Прекратится ли реакция при данной температуре, если все активные молекулы израсходуются (вступят в реакцию)?
(д) Чем отличается активированный комплекс (переходное состояние) от промежуточного продукта сложной реакции? Для ответа изобразите энергетические схемы, как в учебнике Глинки [1, рис. 65; 2, рис. 6.16].
(е) Задачи 338, 340, 345 [3] или 341, 343, 348 [4].
3.3. Лабораторная работа: влияние температуры на скорость реакции
Задачи работы: проверить применимость уравнения Аррениуса на примере реакции тиосульфата натрия с кислотой в растворе, определить её энергию активации. Приветствуется использование личных ноутбуков для обработки результатов измерений.
В данной работе изучается та же реакция, что и в предыдущей, и тем же методом наблюдений, но теперь – в зависимости от температуры, поэтому все исходные концентрации должны быть постоянными.
По итогам предыдущей работы выберите такие концентрации, при которых время помутнения при комнатной температуре составляло бы 40-50 секунд. Если оно будет всего 20 с или меньше, то при повышенных температурах реакция пойдёт так быстро, что будет трудно объективно засечь время помутнения. Чтобы меньше влияли погрешности отмеривания растворов, заготовьте в стакане один общий раствор тиосульфата, откуда потом будете его брать для каждого опыта. Например (цифры условные, но должны быть одинаковыми во всех опытах): по 5 мл раствора кислоты и 15 мл раствора тиосульфата, предварительно разбавленного в пять раз. Этого разбавленного раствора в данном случае надо заготовить 100 мл (с запасом на случай переделки испорченного опыта).
Заранее заготовьте в тетради таблицу для записи результатов, а перед ней оставьте место, где будут указаны использованные во всех опытах объёмы и концентрации растворов.
Зависимость скорости реакции от температуры
| Результаты измерений | Результаты обработки данных | ||||
| t, º C | τ, с | T, K | 1/T, K–1 | 1/τ, с–1 | ln(1/τ) = –ln τ |
Нужно сделать не менее четырёх (ещё лучше пять) опытов при существенно отличающихся температурах: комнатной, ниже комнатной и выше комнатной, с шагом примерно по 10º. Две пробирки с растворами тиосульфата и кислоты выдержите в стакане с водой, подогретой на электроплитке (или в чайнике) или, наоборот, охлаждённой льдом, не менее 10-15 минут, чтобы выровнялись температуры в стакане и в пробирках. Можно параллельно одну пару пробирок охлаждать, а другую нагревать. Температуру воды проверяйте термометром. Затем одну пробирку (где объём раствора меньше) выньте, быстро влейте из неё раствор во вторую, которая остаётся в стакане, и быстро перемешайте. Как и прежде, запишите время τ от момента смешивания до появления первых признаков помутнения и занесите в таблицу.
Рекомендуемый примерный набор температур (но, разумеется, в таблицу надо заносить не эти цифры, а те конкретные температуры, которые были измерены во время протекания реакции):
0º С – вода со льдом и добавкой поваренной соли (раствор замерзает ниже нуля);
12º С – смесь водопроводной и ледяной воды, но без льда;
22º С – комнатная температура;
32º С – водопроводная вода с добавкой кипятка;
42º С – аналогично.
По данным таблицы постройте график. Уравнение Аррениуса экспоненциальное, поэтому график зависимости 1/τ от t или T будет криволинейным. Но на глаз трудно определить тип кривой, например, отличить экспоненту от параболы. Чтобы проверить применимость уравнения Аррениуса, желательно, чтобы теоретический график был прямолинейным. Тогда с первого взгляда видно, лежат ли экспериментальные точки на теоретической прямой.
Для линеаризации применяются координаты Аррениуса: по абсциссе – не температура, а обратная абсолютная температура 1/T, по ординате – не скорость, а логарифм скорости, в данном случае ln(1/τ). Тогда теоретический график выражается прямой с угловым коэффициентом –Ea/k:
ln(1/τ) = lnМ –Ea/k •(1/T),
где k – это постоянная Больцмана, 8, 617•10–5 эВ/К, и энергия активации выражена в эВ в расчёте на один элементарный акт, или прямой с угловым коэффициентом –Ea/R:
ln(1/τ) = lnМ –Ea/R •(1/T),
где R – это газовая постоянная, 8, 314 Дж/(моль•К), и энергия активации выражена в Дж/моль.
Мы фактически измеряем не константу скорости, но некую пропорциональную ей величину, поскольку концентрации во всех опытах постоянны (тепловым расширением жидкого раствора, в отличие от газового, можно пренебречь). Поэтому в уравнении вместо истинного предэкспоненциального множителя А стоит некая пропорциональная ему величина М, но на наклон графика это повлиять не может.
Температура по Цельсию определяется с точностью 2 значащих цифры (например, 25º), но абсолютная температура – уже с тремя (298 К), поэтому и в обратной температуре надо сохранить как минимум три цифры, а лучше четыре, с запасом, чтоб не потерять точность (в данном случае 0, 003356 К–1).
В отличие от предыдущей работы, здесь начало координат не имеет смысла (1/Т=0 – это бесконечная температура), поэтому масштаб выбирайте таким, чтобы весь интервал изменения 1/T и ln(1/τ) занимал длину порядка 10 см.
Для обработки данных очень удобна программа MS Excel и аналогичная программа OpenOffice.org Calc. Там можно не только быстро сделать все необходимые пересчёты, но и построить график, и определить его угловой коэффициент: щелчок правой кнопкой по точке – Добавить линию тренда – Линейная – Параметры – Показывать уравнение на диаграмме.
Таблица цифровых данных в тетради должна быть в любом случае, а угловой коэффициент графика определяется либо из уравнения линии тренда, найденного компьютером, либо из графика, построенного вручную. Для этого нужно провести прямую как можно ближе ко всем экспериментальным точкам, взять её концы (не обязательно экспериментальные точки, если есть разброс) и поделить разность ординат на разность абсцисс (разумеется, не в сантиметрах, а в масштабе графика). Получив угловой коэффициент, можно найти энергию активации. Округлите её до двух значащих цифр: лучшая точность в данной работе недостижима. Если она определена в Дж/моль, то, чтобы не писать незначащие цифры, выразите её в кДж/моль.
В результате работы нужно сделать вывод: применимо ли уравнение Аррениуса к данной реакции (с учётом неизбежных случайных погрешностей), указать величину энергии активации или предложить объяснения, почему в данном случае этого сделать не удалось.
4. Катализ [1, § 60; 2, § 6.2.6]
К изложенному в учебнике необходимо несколько уточнений и добавлений.
Во-первых, реакция в присутствии катализатора идёт не в одну стадию, а минимум в две, как показано ниже на рис. 1 – энергетической диаграмме реакции (в новом издании [2] это учтено). Здесь А и М – условные обозначения исходных веществ и конечных продуктов, а АК – условное обозначение промежуточного продукта с участием катализатора. Соответственно, есть минимум два переходных состояния, ПС1 и ПС2 (а ПС0 – это переходное состояние без катализатора). В случае системы последовательных реакций энергия активации получения конечного продукта определяется самым высоким из промежуточных потенциальных барьеров. В примере на рисунке это ПС1, но в общем случае это не обязательно барьер первой стадии.
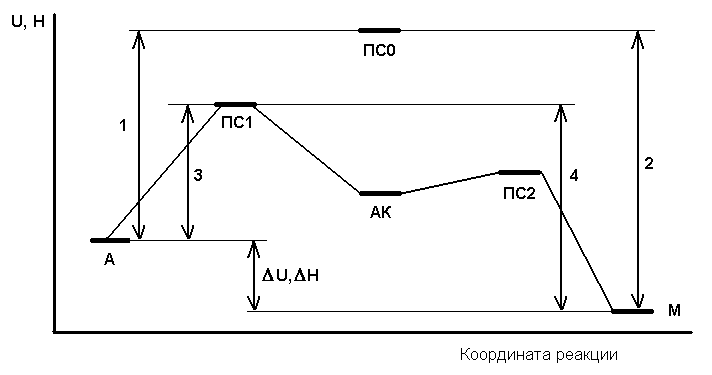
Рис. 1. Энергетическая схема реакции А → М без катализатора
и с катализатором К.
На рис.1 отрезки 1 и 2 – это энергии активации прямой и обратной реакции без катализатора, 3 и 4 – то же с катализатором, Δ U или Δ H – тепловой эффект реакции, выраженный, как изменение внутренней энергии U или энтальпии H (см. § 12.2). В любом случае Еа(прямой) – Еа(обратной) = Δ U или Δ H. На данной схеме реакция экзотермическая (Δ U, Δ H < 0), но это не обязательно.
Принципиально важно, что введение катализатора в любом случае снижает энергию активации и прямой, и обратной реакции на одинаковую величину, и поэтому увеличивает скорость и прямой, и обратной реакции в одинаковое число раз, так что соотношение скоростей в каждый момент остаётся неизменным. В частности, в состоянии равновесия, когда скорость прямой реакции равна скорости обратной, введение катализатора не нарушает этого состояния. Катализатор не смещает равновесие, а лишь ускоряет его достижение.
Во-вторых, важно то, что многие катализаторы действуют избирательно, т.е. ускоряют только одну из нескольких возможных параллельных реакций, причём не всегда самую термодинамически выгодную. Таким образом, правильный подбор катализатора позволяет направлять процессы по желаемому пути.
В третьих, неверно называть ингибиторы – вещества, замедляющие реакцию – отрицательными катализаторами. Если энергия активации процесса с участием ингибитора выше, чем без него, реакция просто не пойдёт по этому пути, её механизм и кинетика останутся прежними. Если же ингибитор препятствует протеканию реакции, значит, он связывается с реагентами или промежуточными продуктами, т.е. расходуется, и это противоречит определению катализатора. Например, ингибиторы цепных реакций окисления масел – это добавки, связывающие свободные радикалы; ингибиторы коррозии металлов – это вещества, связывающиеся с поверхностью металла и затрудняющие доступ агрессивной среды.
Наконец, есть особый случай каталитических реакций – автокатализ, когда катализатором является продукт реакции. Если обычные реакции (каталитические или без катализатора) быстрее всего идут в начальный момент, а потом замедляются, т.к. расходуются реагенты, то автокаталитические реакции идут с самоускорением. В начальный момент, пока катализатор ещё не образовался, реакция идёт медленно. По мере её протекания накапливается катализатор, и реакция ускоряется. Но по мере расходования реагентов реакция неизбежно в конце концов замедлится и прекратится. Следовательно, скорость автокаталитической реакции в функции времени проходит через максимум, а график зависимости концентраций (или количеств) реагентов и продуктов от времени имеет точку перегиба в соответствующий момент (рис. 2).
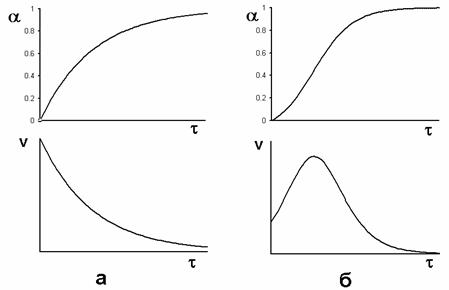
Рис. 2. Так изменяются в функции времени степень превращения α = – Δ C/C0 и скорость реакции v = dα /dτ в случае реакции без катализатора или с заранее введённым катализатором (а) и в случае автокатализа (б). В обоих случаях графики соответствуют реакциям первого порядка.
Примеры автокаталитических реакций:
– растворение меди (или серебра) в растворе азотной кислоты (катализатор – оксид азота): Cu + 4H+ + 2NO3– → Cu2+ + NO2 +2H2O;
– окисление щавелевой кислоты в кислой среде перманганатом калия (катализатор – катион марганца): 5H2C2O4 + 2MnO4– + 6H+ → 10CO2 + 8H2O + 2Mn2+.
Ввиду ограниченного числа лабораторных занятий, практикум по катализу заменяется лекционными демонстрациями. Оба опыта (а) и (б) ниже основаны на разложении пероксида водорода Н2О2 в водном растворе. Это соединение способно практически необратимо разлагаться на воду и кислород: Н2О2 → Н2О + 0, 5О2. В самом деле, мы постоянно имеем кислород в контакте с водой, но пероксид из них не образуется. Правда, и Н2О2 может храниться довольно долго из-за высокого потенциального барьера реакции, но на свету, при нагревании, или в присутствии катализатора разложение происходит быстро. Различие в скоростях наглядно без всяких измерений, по выделению пузырьков газа.
(а) Гетерогенный катализ под влиянием крупинки MnO2. То, что это катализатор, а не реагент, доказывается тем, что крупинка в ходе реакции не исчезает, а объём выделившегося кислорода гораздо больше того, который содержится в твёрдом оксиде. Например, если предположить, что MnO2 отдаёт половину содержащегося в нём кислорода, переходя в MnO, то из одного миллиграмма оксида могло бы получиться лишь около 0, 1 мл кислорода. А реально выделяются десятки и сотни миллилитров, в зависимости от количества взятого пероксида. Однако в этом опыте не видно признаков того, что катализатор вступает в промежуточные реакции. Поэтому делаем следующий опыт.
(б) Гомогенный катализ под влиянием раствора бихромата калия K2Cr2O7. Этот катализатор не столь активен, поэтому для ускорения процесса используем нагревание в стакане с горячей водой. Но чтобы показать эффект катализа, надо обязательно нагревать и такой же раствор пероксида без катализатора. В данном случае по изменению окраски сразу понятно, что бихромат вступает в реакцию. Чтобы доказать, что он не реагент, а катализатор, нужно обязательно дождаться окончания реакции, когда возвращается исходный цвет бихромата.
В этих опытах может также наблюдаться самоускорение реакции, но не от автокатализа, а от саморазогрева. Мы обсуждаем скорости при одинаковой температуре, а реакция экзотермическая, и если теплота не успевает рассеиваться в окружающую среду, то температура повышается, и это даёт дополнительное ускорение.
5. Особенности кинетики гетерогенных реакций [1, § 61; 2, § 6.2.4]