
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы определения порядка химической реакции
|
|
1) Интегральные методы
Методы подстановки. Значения концентрации (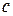 ) или аналогичные ей величины: парциальное давление (
) или аналогичные ей величины: парциальное давление (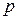 ), угол вращения плоскости поляризации (
), угол вращения плоскости поляризации (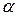 ) в данный момент времени подставляют в уравнения первого, второго, третьего порядка. Порядок реакции определяется тем уравнением, в котором расчет (
) в данный момент времени подставляют в уравнения первого, второго, третьего порядка. Порядок реакции определяется тем уравнением, в котором расчет (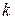 ) дает постоянную величину в различные моменты времени.
) дает постоянную величину в различные моменты времени.
Графические методы. Значения концентрации в соответствующий момент времени представляют в виде графика. Линейная зависимость концентрации от времени в соответствующих координатах определяет порядок реакции.
Например:

По периоду полураспада (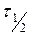 ).(Частный случай метода Оствальда – Нойеса).
).(Частный случай метода Оствальда – Нойеса).
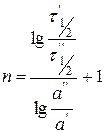 ,
,
где 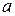 - исходная концентрация вещества.
- исходная концентрация вещества.
Можно использовать также построение графика.


2) Дифференциальные методы
Метод Вант – Гоффа. Расчет порядка реакции можно провести по уравнению
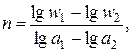
Если использовать выражение 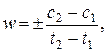 то в знаменателе средние концентрации
то в знаменателе средние концентрации 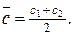
Следует учесть, что для реакции первого порядка 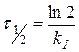 ,
,
для реакции второго порядка 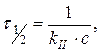
а для реакции третьего порядка 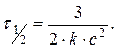
Выражение для константы скорости реакции различных порядков следующее:
первый порядок 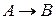

второй порядок  :
:
а) исходные концентрации веществ одинаковы
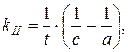
б) исходные концентрации веществ неодинаковы
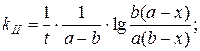
третий порядок (концентрации исходных веществ одинаковы)
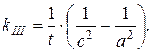
В этих уравнениях 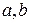 - исходные концентрации веществ,
- исходные концентрации веществ,
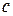 - концентрация в данный момент времени,
- концентрация в данный момент времени,
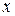 - количество прореагировавшего вещества.
- количество прореагировавшего вещества.