Задание на лабораторную работу

Лабораторная работа

Систематический обход графа методами «в глубину» и «в ширину»

Цель работы: получить навыки реализации алгоритмов обхода графов.

6.1. Используемый теоретический материал.

Проанализируем два базовых алгоритма, которые используются как основа для построения многих других. Это «поиск в ширину» и «поиск в глубину».

При разборе примеров применения алгоритмов будем использовать следующие наглядные обозначения. Будем считать, что до начала работы алгоритма все вершины белые. Если вершина в ходе работы алгоритма встречается первый раз – она изменяет цвет на серый. Если вершина обработана и удалена из очереди – она становится чёрной.

Для заданного графа G = (V, E) и фиксированной начальной вершины s алгоритм «поиска в ширину» перечисляет все достижимые из s (если проходить по рёбрам) вершины в порядке возрастания расстояния от s.

Расстоянием считается длина (число рёбер) кратчайшего пути. В процессе поиска из графа выделяется часть, называемая «деревом поиска в ширину» с корнем s. Она содержит все достижимые из s вершины (и только их). Для каждой из них путь из корня в дереве поиска будет одним из кратчайших путей (из начальной вершины) в графе. Алгоритм применим и к ориентированным и к неориентированным графам.

Реализация алгоритма под названием BFS использует представление графа G = (V, E) списками смежных вершин. Для каждой вершины u графа дополнительно хранятся её цвет и её предшественник – p (u). Кроме того, хранится d (u) – расстояние от s до u.

Вторым базовым алгоритмом для графов является «поиск в глубину». Алгоритм поиска в глубину перечисляет вершины начиная от начальной и уходя по рёбрам «вглубь» графа. Дойдя до тупиковой вершины, из которой нет пути по непройденному ребру, надо возвратиться и искать другой путь.

Так делается, пока не обнаружены все вершины, достижимые из начальной.

Если после этого остаются необнаруженные вершины, можно выбрать одну из них и повторять процесс, пока не будут перечислены все вершины графа.

Алгоритм «поиска в глубину» также хранит цвета вершин. Кроме того, некоторые реализации «поиска в глубину» ставят на вершинах метки времени. Каждая вершина имеет две метки: в d (v) записано, когда эта вершина была обнаружена (и сделана серой), а в f (v) – когда была закончена обработка списка смежных с v вершин (и v стала чёрной). Эти метки используются во многих алгоритмах на графах и полезны для анализа свойств «поиска в глубину».

Реализация «поиска в глубину» под названием DFS использует метки времени.

Задание на лабораторную работу

Написать программу, реализующую алгоритмы обхода графа «в глубину» и «в ширину».

Варианты заданий

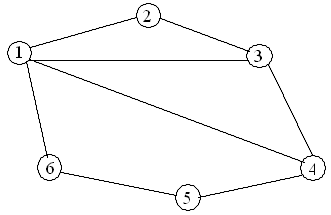
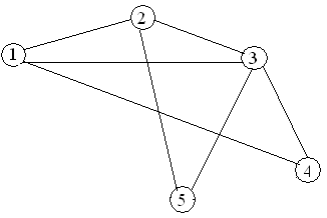
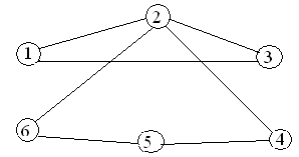
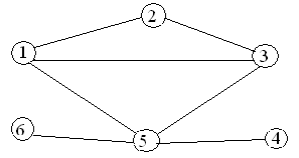
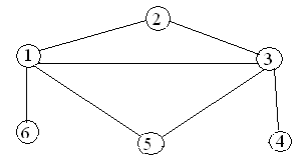
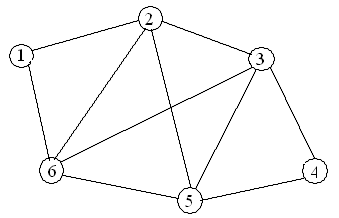
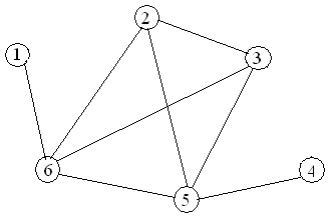
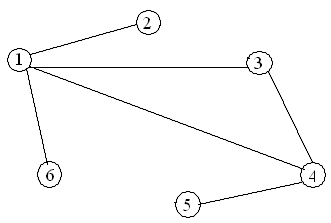
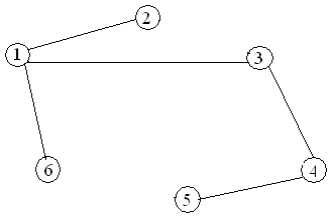
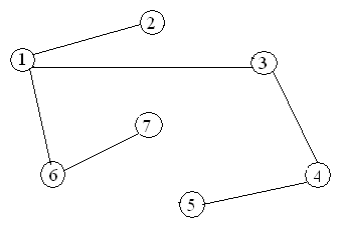
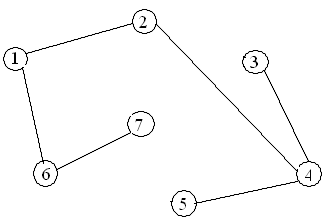
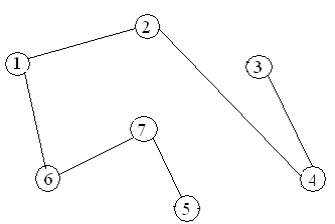
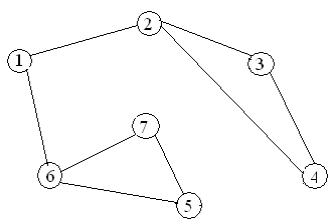
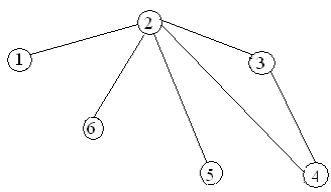
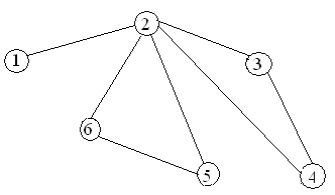
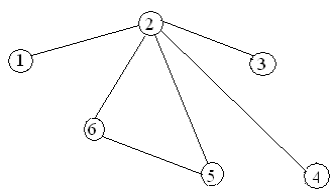
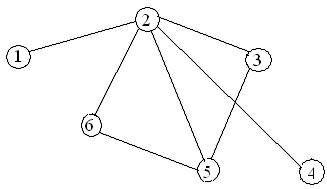
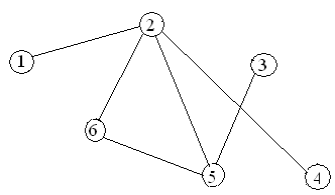
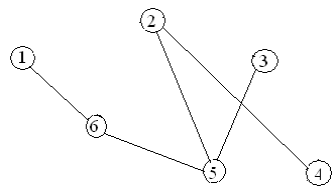
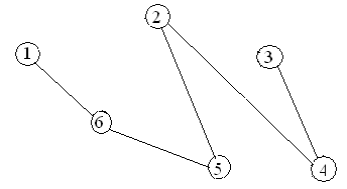
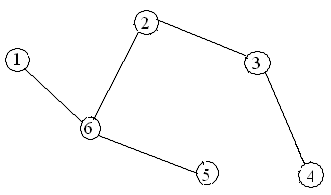
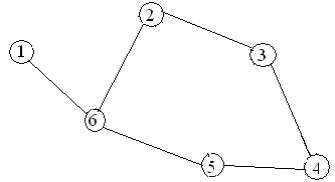
Содержание отчета

Для защиты лабораторной работы необходимо представить отчет,

содержащий код программы и результат работы программы для

выполненного варианта.