
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Представление регрессии в корреляционной форме. Частные корреляции
|
|
Пусть методом наименьших квадратов требуется построить модель вида
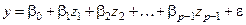 , (1)
, (1)
где 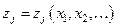 – некоторые функции предикторов
– некоторые функции предикторов 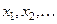 . Было проведено
. Было проведено 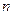 наблюдений, значения которых составляют вектор
наблюдений, значения которых составляют вектор 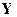 :
:
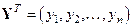 .
.
Вычислим значения 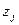 в каждой из
в каждой из 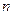 точек и составим матрицу
точек и составим матрицу 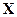 :
:
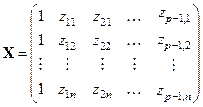 .
.
Найдем средние значения элементов вектора 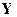 и каждого из столбцов матрицы
и каждого из столбцов матрицы 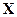 , начиная со второго. Обозначим эти величины
, начиная со второго. Обозначим эти величины 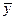 ,
, 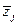 .
.
Рассчитаем 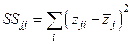 ,
, 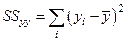 .
.
Перепишем модель (1) в виде
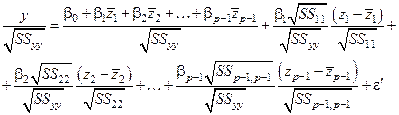 , (2)
, (2)
и введем обозначения
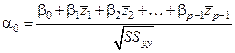 ,
, 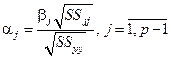 (3)
(3)
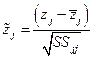 . (4)
. (4)
Подставив формулы (3), (4) в выражение (2), получим:
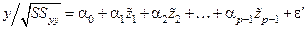 . (5)
. (5)
Если составить сумму квадратов
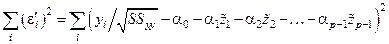
и продифференцировать ее по 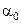 , получим первое нормальное уравнение
, получим первое нормальное уравнение
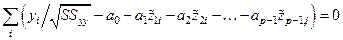
или
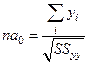 ,
,
так как 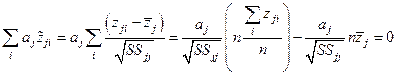 ,
, 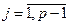 .
.
Таким образом, оценка свободного члена модели (5) всегда будет равна 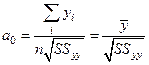 независимо от того, каковы будут значение других коэффициентов. Поэтому
независимо от того, каковы будут значение других коэффициентов. Поэтому 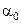 можно исключить из модели (5) и применять ее в виде
можно исключить из модели (5) и применять ее в виде
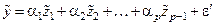 , (6)
, (6)
где 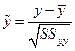 . Эта модель связывает нормированные переменные
. Эта модель связывает нормированные переменные  ,
, 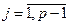 , с нормированным откликом
, с нормированным откликом 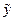 и содержит
и содержит 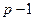 неизвестных коэффициентов. Для нахождения их оценок воспользуемся методом наименьших квадратов. Составим матрицы
неизвестных коэффициентов. Для нахождения их оценок воспользуемся методом наименьших квадратов. Составим матрицы 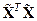 и
и 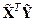 :
:
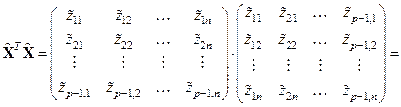
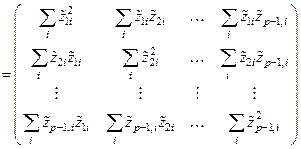
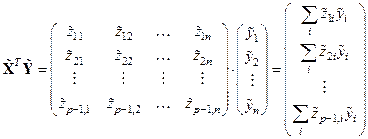
Рассмотрим суммы 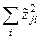 ,
, 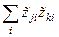 и
и 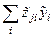 :
:
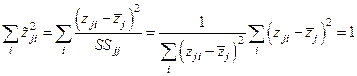 ,
,
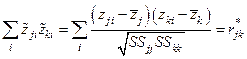 ,
, 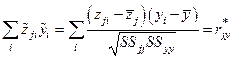 .
.
Внедиагональные члены матрицы 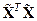 и элементы вектора
и элементы вектора 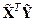 представляли бы собой выборочные коэффициенты корреляции величин
представляли бы собой выборочные коэффициенты корреляции величин 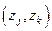 и
и 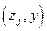 , если бы эти величины имели двумерное распределение. Несмотря на то, что это не так, значения
, если бы эти величины имели двумерное распределение. Несмотря на то, что это не так, значения 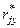 и
и 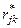 позволяют судить о наличии точной или приближенной парной линейной зависимости между конкретными наборами данных
позволяют судить о наличии точной или приближенной парной линейной зависимости между конкретными наборами данных 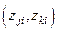 и
и 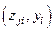 . Матрица
. Матрица 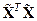 для преобразованной модели в дальнейшем будет называться корреляционной матрицей
для преобразованной модели в дальнейшем будет называться корреляционной матрицей 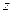 -переменных, а
-переменных, а 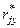 и
и 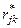 – коэффициентами корреляции, хотя более корректно вместо слова «корреляция» использовать термин «сопряженность», так величины
– коэффициентами корреляции, хотя более корректно вместо слова «корреляция» использовать термин «сопряженность», так величины 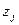 являются детерминированными.
являются детерминированными.
Система нормальных уравнений для модели (6) будет иметь вид:
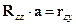 ,
,
где
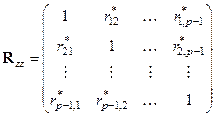 ,
, 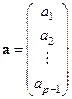 ,
, 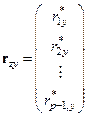 . (7)
. (7)
После того, как найдены оценки 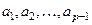 , можно перейти к оценкам
, можно перейти к оценкам 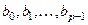 по соотношениям:
по соотношениям:
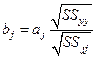 ,
, 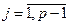 ;
; 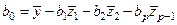
Проверка гипотезы 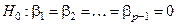 равноценна проверке гипотезы
равноценна проверке гипотезы 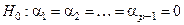 . При этом надо учитывать, что остаточная сумма квадратов преобразованной модели будет иметь
. При этом надо учитывать, что остаточная сумма квадратов преобразованной модели будет иметь 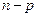 степеней свободы (как для исходной модели), так как нормированные переменные связаны ограничением
степеней свободы (как для исходной модели), так как нормированные переменные связаны ограничением 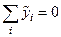 .
.
Преобразование регрессионной задачи к виду (6) удобно, так как оно делает все числа, участвующие в вычислениях, лежащими между -1 и 1. Это минимизирует эффекты ошибок округления и делает вычисления более устойчивыми. С другой стороны, корреляционная матрица полезна для выявления тех функций факторов 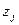 , между которыми существует линейная или очень близкая к линейной связь. Если для некоторых
, между которыми существует линейная или очень близкая к линейной связь. Если для некоторых 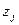 ,
, 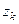
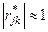 , то следует один из этих членов исключить из модели. Выбор, какой из членов следует оставить в модели, может осуществляться на основании знаний или интуитивных представлений о каждом из них. Если нет иных оснований, то в модель включается тот член, для которого показатель величины связи с откликом (коэффициент корреляции с откликом) больше.
, то следует один из этих членов исключить из модели. Выбор, какой из членов следует оставить в модели, может осуществляться на основании знаний или интуитивных представлений о каждом из них. Если нет иных оснований, то в модель включается тот член, для которого показатель величины связи с откликом (коэффициент корреляции с откликом) больше.
Корреляционная матрица используется также в различных методах выбора факторов. В этой ситуации возникает потребность в определении частных (парциальных) коэффициентов корреляции.
Рассмотрим модель
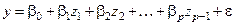
и, используя результаты эксперимента, найдем корреляционную матрицу 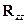 и вектор
и вектор 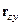 .
.
Если построить модели
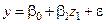 ,
, 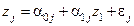 ,
, 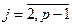 , (8)
, (8)
то можно найти новые независимые переменные 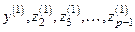 , значения которых равны остаткам от регрессии
, значения которых равны остаткам от регрессии 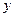 на
на 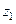 ,
, 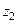 на
на 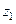 , …,
, …, 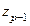 на
на 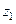 . (остатки от подобранных моделей (18)).
. (остатки от подобранных моделей (18)).
Значения новых независимых переменных 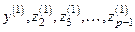 представляют собой долю исходных данных, которые не зависят от значений
представляют собой долю исходных данных, которые не зависят от значений 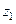 . Теперь можно построить новую корреляционную матрицу
. Теперь можно построить новую корреляционную матрицу 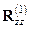 для переменных
для переменных 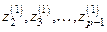 и новый вектор корреляций
и новый вектор корреляций 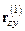 . Они состоят из частных коэффициентов корреляции. Частный коэффициент корреляции может записываться, например, так
. Они состоят из частных коэффициентов корреляции. Частный коэффициент корреляции может записываться, например, так 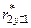 . Это означает «частный коэффициент корреляции переменных
. Это означает «частный коэффициент корреляции переменных 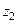 и
и 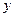 после исключения влияния переменной
после исключения влияния переменной 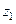 ».
».
Аналогично, если построить модели
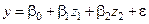 ,
, 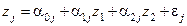 ,
, 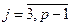 , (9)
, (9)
то можно определить остатки от регрессий 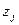 ,
,  , на
, на 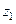 ,
, 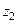 и
и 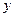 на
на 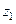 ,
, 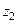 и построить корреляционную матрицу
и построить корреляционную матрицу 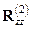 и вектор корреляций
и вектор корреляций 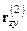 . Этот процесс можно продолжать далее.
. Этот процесс можно продолжать далее.
Частные коэффициенты корреляции можно находить по формулам
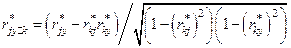 , (10)
, (10)
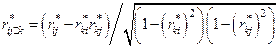 (11)
(11)
и так далее.