
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные теоретические положения
|
|
Измерения, при котором искомое значение величин находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, называются косвенным.
Допустим, определяется величина путем непосредственного измерения величин x1, x2, …, xm, с которыми связана зависимость
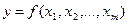
| (2.1) |
Если результаты прямых измерений x1, x2, …, xm содержат случайные погрешности, они являются случайными величинами и поэтому величину, измеренную косвенно путем вычислений по результатам прямых измерений, нужно рассматривать, как функцию случайных величин. Среднее значение результата косвенных измерений находят подстановкой в функциональную зависимость (2.1) средних значений результатов прямых измерений:
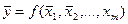
| (2.2) |
Среднеквадратичное отклонение случайной погрешности косвенного измерения:

| (2.3) |
Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений, а их среднестатистические получены обработкой достаточно большого числа результатов.
Если же объемы рядов прямых измерений недостаточно велики, можно воспользоваться распределением Стьюдента с некоторым " Эффективным" числом степеней свободы, которые при независимости погрешности подсчитываются по формуле:
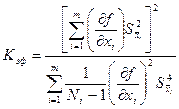
| (2.4) |
Кэф – характеризует количество измерений для y.
По значению Кэф и вероятности попадания в доверительный интервал Р находим коэффициент Стьюдента tp. Тогда доверительный интервал определяется следующим образом:
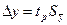
| (2.5) |
и результат косвенного измерения можно записать в виде:
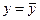 : Δ от – Δ у до + Δ у; Р=0, 95 : Δ от – Δ у до + Δ у; Р=0, 95
| (2.6) |
Математическое ожидание результата косвенных измерений не равно истинному значению измеряемой величины, т.е. оценка (2.2) является смещенной, если хотя бы одна вторая частная производная уравнения (2.1) отличается от 0 и погрешность результата косвенного измерения наряду со случайной, содержит систематическую составляющую.
Если погрешность измерения аргумента некоррелированы, эта систематическая погрешность определяется как:
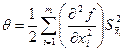
| (2.7) |
Для того чтобы исключить систематическую погрешность, нужно к рассчитанному по формуле (2.2) результату прибавить поправку q, равную систематической погрешности по величине и обратную ей по знаку. Результаты п измерений величины x обрабатываются следующим образом:
1. Определяют среднеарифметическое ряда наблюдений
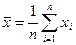
| (2.8) |
2. Вычисляют случайные отклонения результатов наблюдений
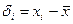
| (2.9) |
3. Вычисляют оценку среднеквадратичного отклонения ряда наблюдений
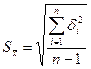
| (2.10) |
4. Вычисляют оценку среднеквадратичного отклонения результатов прямых измерений
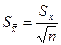
| (2.11) |