
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выполнение работы. I. Система , дифференциальных уравнения, представлявшая кинетическую модель данной химической реакции:
|
|
I. Система, дифференциальных уравнения, представлявшая кинетическую модель данной химической реакции:
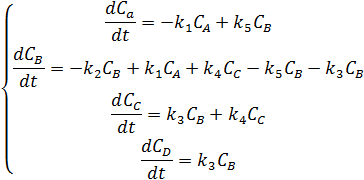
2. Расчетные формулы метода Эйлера:
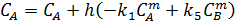
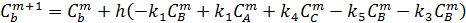
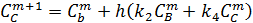
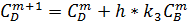
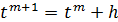
3. Результаты численного решения системы дифференциальных уравнений на калькуляторе. h= 0, 2; 5 шагов по времени.
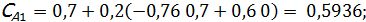
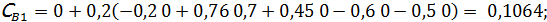

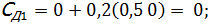
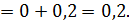
Таблица результатов расчета
| № | СА | СВ | СС | СД | |
| Q | 0, 7 | ||||
| I | 0, 2 | 0, 5936 | 0, 1064 | ||
| 0, 4 | 0, 5161 | 0, 1541 | 0, 0192 | 0, 0106 | |
| 0.6 | 0, 4562 | 0, 1726 | 0, 0452 | 0, 0260 | |
| 0, 8 | 0, 4076 | 0, 1770 | 0, 0722 | 0, 0433 | |
| I | 0, 3669 | Q.I747 | 0, 0976 | 0, 0610 |
5. ПРОГРАММА МЕТОДОВ:
1. Эйлера;
2. Эйлера-Коши;
3. Рунге-Кутта 2-го порядка;
4. Рунге-Кутта 4-го порядка.
1)
Program EULER;
const
eps = 1e-5;
x0 = 3;
y0 = 3;
type
TFunc = function(x, y: extened): extended;
function func(x, y: extended): extended; far;
begin
func: = y*cos(x) - 2*sin(2*x);
end;
function Euler(f: TFunc; x0_, x_end, y0_: extended; n: word): extended;
{ где x0_ и y0_ - начальное условие
x_end - точка, в которой необходимо вычислить результат
n - количество шагов для вычисления результата }
var
i: word; { счетчик цикла }
x, h: extended; { текущая точка и длина шага }
res: extended; { переменная для накопления конечного результата функции}
begin
h: = (x_end - x0_)/n; { Находим длину шага }
res: = y0_; { устанавливаем начальные значения}
x: =x0_;
for i: =1 to n do
begin { вычисляем результат по методу Эйлера }
res: =res+h*f(x, res);
x: =x+h; { переходим к следующей точке }
end;
Euler: =res; { присваиваем конечный результат функции }
end;
begin
writeln('Численное решение дифференциальных уравнений: ');
writeln(#10, ' y'' = y*cos(x) - 2*sin(2*x); y(0)=3; x_end=', (5*x0+3.5): 5: 5);
writeln(#10, 'Метод Эйлера: ');
writeln('n=5 000, result: ', Euler(func, x0, 5*x0+3.5, y0, 5000): 5: 5);
writeln('n=10 000, result: ', Euler(func, x0, 5*x0+3.5, y0, 10000): 5: 5);
writeln('n=25 000, result: ', Euler(func, x0, 5*x0+3.5, y0, 25000): 5: 5);
write(#10, 'Press Enter to continue.');
readln;
end.
2)
Program EULER-KOSHI;
const
eps = 1e-5;
x0 = 3;
y0 = 3;
type
TFunc = function(x, y: extened): extended;
function func(x, y: extended): extended; far;
begin
func: = y*cos(x) - 2*sin(2*x);
end;
function Euler2(f: TFunc; x0_, x_end, y0_: extended; n: word): extended;
{ где x0_ и y0_ - начальное условие
x_end - точка, в которой необходимо вычислить результат
n - количество шагов для вычисления результата }
var
i: word; { счетчик цикла }
x, h: extended; { текущая точка и длина шага }
res: extended; { переменная для накопления конечного результата функции}
begin
h: = (x_end - x0_)/n; { Находим длину шага }
res: = y0_; { устанавливаем начальные значения}
x: =x0_;
for i: =1 to n do
begin { вычисляем результат по исправленному методу Эйлера }
res: =res+h*(f(x, res)+f(x+h, res+h*f(x, res)))/2;
x: =x+h; { переходим к следующей точке }
end;
Euler2: =res; { присваиваем конечный результат функции }
end;
begin
writeln(#10, 'Эйлера-Коши: ');
writeln('n=50, result: ', Euler2(func, x0, 5*x0+3.5, y0, 50): 5: 5);
writeln('n=100, result: ', Euler2(func, x0, 5*x0+3.5, y0, 100): 5: 5);
writeln('n=250, result: ', Euler2(func, x0, 5*x0+3.5, y0, 250): 5: 5);
write(#10, 'Press Enter to continue.');
readln;
end.
3)
Program RK2;
const
eps = 1e-5;
x0 = 3;
y0 = 3;
type
TFunc = function(x, y: extened): extended;
function func(x, y: extended): extended; far;
begin
func: = y*cos(x) - 2*sin(2*x);
end;
function Euler3(f: TFunc; x0_, x_end, y0_: extended; n: word): extended;
{ где x0_ и y0_ - начальное условие
x_end - точка, в которой необходимо вычислить результат
n - количество шагов для вычисления результата }
var
i: word; { счетчик цикла }
x, h: extended; { текущая точка и длина шага }
res: extended; { переменная для накопления конечного результата функции}
begin
h: = (x_end - x0_)/n; { Находим длину шага }
res: = y0_; { устанавливаем начальные значения}
x: =x0_;
for i: =1 to n do
begin { вычисляем результат по модифицированному методу Эйлера }
res: =res+h*f(x+h/2, res+(h/2)*f(x, res));
x: =x+h; { переходим к следующей точке }
end;
Euler3: =res; { присваиваем конечный результат функции }
end;
begin
writeln(#10, 'Метод Рунге-Кутта 2: ');
writeln('n=50, result: ', Euler3(func, x0, 5*x0+3.5, y0, 50): 5: 5);
writeln('n=100, result: ', Euler3(func, x0, 5*x0+3.5, y0, 100): 5: 5);
writeln('n=250, result: ', Euler3(func, x0, 5*x0+3.5, y0, 250): 5: 5);
write(#10, 'Press Enter to continue.');
readln;
end.
4)
Program RK4;
const
eps = 1e-5;
x0 = 3;
y0 = 3;
type
TFunc = function(x, y: extened): extended;
function func(x, y: extended): extended; far;
begin
func: = y*cos(x) - 2*sin(2*x);
end;
function RungeKutt(f: TFunc; x0_, x_end, y0_: extended; n: word): extended;
{ где x0_ и y0_ - начальное условие
x_end - точка, в которой необходимо вычислить результат
n - количество шагов для вычисления результата }
var
i: word; { счетчик цикла }
x, h: extended; { текущая точка и длина шага }
res: extended; { переменная для накопления конечного результата функции }
k1, k2, k3, k4: extended; { вспомогательные переменные вычисления результата }
begin
h: = (x_end - x0_)/n; { Находим длину шага }
res: = y0_; { устанавливаем начальные значения}
x: =x0_;
for i: =1 to n do
begin { вычисляем результат по методу Рунге-Кутта 4го порядка }
k1: =f(x, res);
k2: =f(x+h/2, res+h*k1/2);
k3: =f(x+h/2, res+h*k2/2);
k4: =f(x+h, res+h*k3);
res: =res+h*(k1+2*k2+2*k3+k4)/6;
x: =x+h; { переходим к следующей точке }
end;
RungeKutt: =res; { присваиваем конечный результат функции }
end;
begin
writeln(#10, 'Метод Рунге-Кутта 4: ');
writeln('n=50, result: ', RungeKutt(func, x0, 5*x0+3.5, y0, 50): 5: 5);
writeln('n=100, result: ', RungeKutt(func, x0, 5*x0+3.5, y0, 100): 5: 5);
writeln('n=250, result: ', RungeKutt(func, x0, 5*x0+3.5, y0, 250): 5: 5);
write(#10, 'Press Enter to continue.');
readln;
end.