Элементы общей теории искажений.

Качество карты определяется в значительной степени величиной и характером искажений. Эти показатели являются основными при решении вопроса о выборе картографической проекции для составления морской карты.

Для анализа искажений, присущих той или иной карте, пользуются эллипсом искажений, который получается следующим образом. В любом месте на поверхности земного сфероида можно выбрать малый круг такого радиуса r₀, в пределах которого эллипсоидальная поверхность является практически плоской. Проекция этого круга на другую плоскость всегда будет эллипсом, а проекция любой прямой, находящейся в пределах данного круга, будет также прямой в пределах полученного эллипса (рис.8).

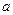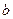Отношения полуосей и эллипса к радиусу r₀ соответствующего круга на поверхности земного сфероида равны частным масштабам карты в данных точках по данным направлениям. Причем отношение большей полуоси эллипса к кругу будет максимальным частным масштабом карты в данной точке, отношение меньшей полуоси эллипса к радиусу круга – минимальным частным масштабом.

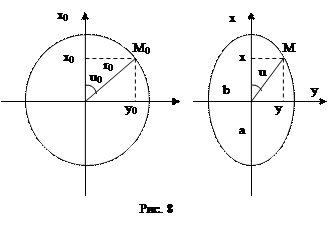
Направления, по которым частный масштаб карты достигает экстремальных значений, называется главным направлением. На всех морских картах главные направления совпадают с направлениями меридианов и параллелей. Частный масштаб вдоль меридиана принято обозначать m, а вдоль параллели – n. При таком расположении эллипса искажений, как показано на рис. 8,

m = 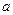/ r₀; n = b / r₀.

Определим, каковы должны быть масштабы карты по главным направлениям, чтобы углы на карте были равны соответствующим углам на местности, т.е. при каких условиях проекция будет равноугольной.

Пусть ось х на земном сфероиде и направление х большой полуоси эллипса искажений на карте совпадают с направление меридиана (см. рис.8). Выберем на окружности произвольную точку М₀ обозначим U₀, тогда

.

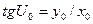На карте для соответствующей точки М

.

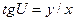Учитывая, что 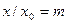и 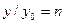, получим

; .

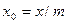Следовательно

.
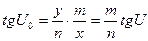