
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное распределение
|
|
Непрерывная случайная величина X имеет нормальное распределение, если ее плотность распределения вероятности имеет вид:
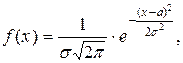
где 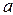 и
и 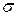 – параметры распределения, причем
– параметры распределения, причем 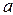 = M (X),
= M (X), 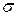 =
= 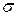 (X).
(X).
График дифференциальной функции распределения называют нормальной кривой, или кривой Гаусса (рис.1).
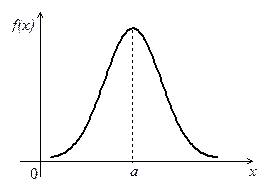
Рис.1
Если 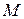 (X) = 0,
(X) = 0, 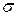 (X) = 1, то нормально распределенная случайная величина называется нормированной, ее дифференциальная функция распределения
(X) = 1, то нормально распределенная случайная величина называется нормированной, ее дифференциальная функция распределения 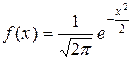 табулирована.
табулирована.
Вероятность попадания нормально распределенной случайной величины в интервал (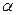 ,
, 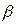 ) находим по формуле:
) находим по формуле:
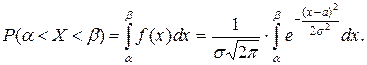
Данный интеграл выражается через функцию Лапласа, которую еще называют интегралом вероятностей и обозначают Ф (t):
Ф (t) 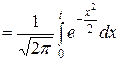 .
.
Функция Лапласа – это вероятность попадания нормированной нормально распределенной случайной величины в интервал (0, t).
Функция Лапласа обладает следующими свойствами:
1. Ф (0) = 0.
2. Ф (– t) = – Ф (t), то есть она нечетная.
3. Ф (¥) = 0, 5 (практически уже при t > 4).
Функция Ф (t) табулирована (см. прил. 2).
Применяя функцию Лапласа, получим:
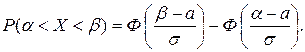
При решении задач часто возникает необходимость определения вероятности отклонения нормально распределенной случайной величины от ее математического ожидания:
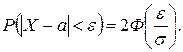
Пример 1. Средний процент выполнения плана некоторыми предприятиями составляет 105 %, среднее квадратическое отклонение – 5 %. Полагая, что выполнение плана предприятиями подчинено закону нормального распределения, вычислить долю предприятий, выполняющих план от 110 до 130 %, то есть определить вероятность попадания рассматриваемой величины в интервал (110, 130).
Решение. Случайная величина X – выполнение плана предприятиями; она имеет нормальное распределение с параметрами:
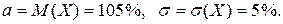 Для нахождения искомой вероятности воспользуемся формулой:
Для нахождения искомой вероятности воспользуемся формулой:
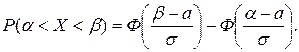
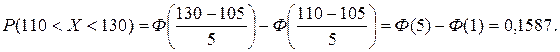
Пример 2. Длина изготовляемой детали представляет собой случайную величину, распределенную по нормальному закону. Средняя длина детали равна 50 мм, а дисперсия – 0, 25 мм2. Какое поле допуска длины изготовляемой детали можно гарантировать с вероятностью 0, 99?
Решение. Длина изготовляемой детали – случайная величина X, имеющая нормальный закон распределения с параметрами:
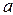 =
= 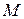 (X) = 50 мм,
(X) = 50 мм, 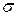 =
= 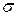 (X) =
(X) = 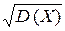 = 0, 5.
= 0, 5.
Известна вероятность, гарантирующая некоторое поле допуска, то есть Р (a< X < b) = 0, 99. Чтобы найти это поле допуска, воспользуемся формулой:
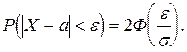
Неравенство ½ X – 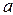 ½ < e эквивалентно неравенству
½ < e эквивалентно неравенству 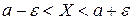 , следовательно, и равновероятно, то есть
, следовательно, и равновероятно, то есть 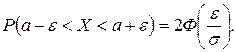
Исходя из условия задачи, можем записать:
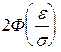 = 0, 99;
= 0, 99; 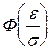 = 0, 495.
= 0, 495.
По таблице значений функции Лапласа (см. прил. 2) находим 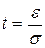 = 2, 58.
= 2, 58.
Отсюда e = 2, 58 × 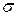 = 1, 29, тогда 50 – 1, 29 £ X £ 50 + 1, 2 или 48, 71 £ X £ 51, 29.
= 1, 29, тогда 50 – 1, 29 £ X £ 50 + 1, 2 или 48, 71 £ X £ 51, 29.
|