
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Потеря устойчивости центрально сжатых стержней
|
|
При увеличении силы Р стержень вначале будет оставаться прямым, если ему дать искусственное отклонение У, то после устранения причины отклонения он вернется к первоначальному положению (устойчивое равновесие). При увеличении внешней нагрузки Р могут быть возможны прямолинейная форма равновесия стержня и криволинейная, изгибная. В этом случае при небольшом искусственном отклонении стержня на величину У и устранения причины отклонения стержень останется изогнутым. В точке разветвления прямолинейной криволинейной форм равновесия внешняя сила достигнет своего критического значения Nсч. Самое незначительное увеличение силы Nсч ведет к резкому нарастанию деформаций и потере несущей способности стержня. Критическая сила определяется по формуле Л. Эйлера:
|
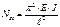 , где Е – модуль упругости материала стержня; J – минимальный момент инерции сечения стержня;
, где Е – модуль упругости материала стержня; J – минимальный момент инерции сечения стержня; 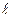 – расчетная длина стержня.
– расчетная длина стержня.
Критические напряжения в стержне:
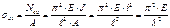 ,
,
Где А- площадь брутто поперечного сечения стержня; 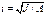 – радиус инерции стержня;
– радиус инерции стержня; 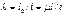 - гибкость стержня, где μ -коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня;
- гибкость стержня, где μ -коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня; 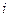 – радиус инерции сечения стержня;
– радиус инерции сечения стержня;  - расчетная длина стержня; l - геометрическая длина стержня.
- расчетная длина стержня; l - геометрическая длина стержня.
Критические напряжения зависят только от гибкости стержня l. Минимальная гибкость для стального стержня, выше которой формула Эйлера будет справедлива:
для мягких сталей 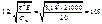 , для сталей повышенной прочности λ ≥ 85.
, для сталей повышенной прочности λ ≥ 85.
На практике гибкость центрально сжатых стержней составляет примерно половину указанных предельных, то есть стержни устраиваются настолько жесткими, что выпучивание наступает лишь после появления пластических деформаций. В этом случае
 , где Т – приведенный модуль продольного изгиба, зависящий от касательного модуля Е1.
, где Т – приведенный модуль продольного изгиба, зависящий от касательного модуля Е1.
Устойчивость центрально сжатого стержня будет обеспечена, если напряжение в нем будут меньше критических:
 , где φ - коэффициент устойчивости
, где φ - коэффициент устойчивости
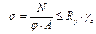 .
.