
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция света
|
|
Под интерференцией света обычно понимают широкий круг явлений, в которых при наложении световых волн результирующая интенсивность не равна сумме интенсивностей отдельных волн: в одних местах она больше, в других – меньше, т.е. возникают чередующиеся светлые и темные участки – интерференционные полосы. Другими словами, интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн.
В дальнейшем под интенсивностью световой монохроматической волны будем понимать следующую величину, определяемую формулой:
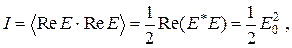 (5.1)
(5.1)
где E 0 – действительная амплитуда световой волны.
Рассмотрим суперпозицию двух линейно поляризованных в одном направлении волн с различными амплитудами:
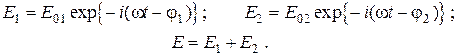 (5.2)
(5.2)
Тогда суммарная интенсивность I будет равна:
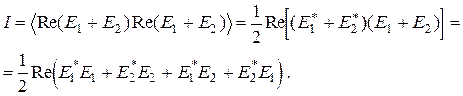 (5.3)
(5.3)
С учетом (5.1) и (5.2) выражение (5.3) принимает вид:
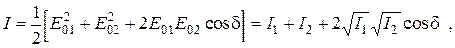 (5.4)
(5.4)
где 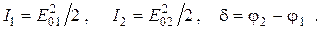
Если частоты интерферирующих волн различны, то формула (5.4) примет вид:
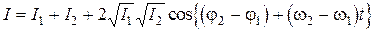 . (5.5)
. (5.5)
Последнее слагаемое в (5.4) или в (5.5) называется интерференционным членом. В тех случаях, когда он обращается в нуль, результирующая интенсивность равна сумме интенсивностей отдельных волн и интерференция отсутствует. Если же интерференционный член отличен от нуля, то суммарная интенсивность изменяется от минимального значения
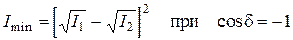 (5.6)
(5.6)
до максимального значения
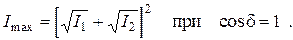 (5.7)
(5.7)
Монохроматических волн в природе не существует, поэтому приходится ограничиться квазимонохроматическими волнами. Картина интерференции монохроматических волн является лишь первым приближением в интерференции волн от реальных источников. Существующие экспериментальные методы получения интерференционной картины обычно делятся на два класса: 1) способы деления амплитуды волны; 2) способы деления фронта волны.
Рассмотрим несколько примеров.
Интерферометр Майкельсона. Интерферометр состоит из делительной пластинки P и двух зеркал R 1и R 2, расположенных на расстояниях l 1 и l 1 от пластины (рис.5.1). На пластинке P происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения. Нетрудно показать, что при любом коэффициенте отражения света от пластинки амплитуды полей, приходящих в точку наблюдения А одинаковы. Т.к. частоты также остаются постоянными, то (5.5) принимает вид:
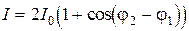 , (5.8)
, (5.8)
где I 0 – интенсивность каждой из интерферирующих волн.При этом интенсивность I изменяется от своего минимального значения при 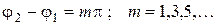 до своего максимального значения при
до своего максимального значения при 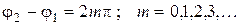 . Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:
. Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:
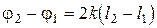 . (5.9)
. (5.9)
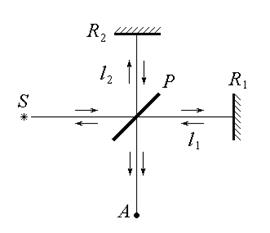 Рис. 5.1
Рис. 5.1
|
Пример применения интерферометра Майкельсона. При движении одного из зеркал за счет продольного эффекта Доплера происходит смещение частоты отраженной волны:
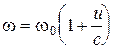 . (5.10)
. (5.10)
Тогда существенной станет не постоянная амплитуда, а периодически изменяющаяся с частотой в соответствии со значением скорости движения зеркала:
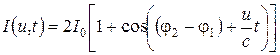 . (5.11)
. (5.11)
Как видно, интерферометр Майкельсона – прекрасный инструмент не только для измерений расстояний, но и скорости перемещения объектов, т.к. он весьма чувствителен к перемещениям.
Поставив в одно из плеч призму или линзу, можно получить великолепный инструмент для исследования их качества по интерференционной картине (интерферометр Тваймана–Грина).
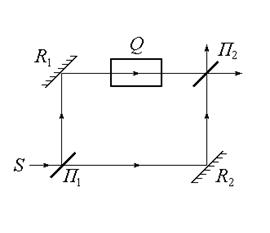 Рис. 5.2
Рис. 5.2
|
Другой пример интерферометра по методу деления амплитуды – интерферометр Маха–Цендера (рис.5.2). По изменению интерференционной картины и длине пути светового пучка в ячейке Q можно с большой точностью определить относительный показатель преломления исследуемого вещества ячейки.
Принцип Гюйгенса. При обосновании волновой теории Гюйгенс предложил принцип, позволивший наглядно интерпретировать ряд волновых задач: если в некоторый момент времени задан фронт световой волны, то для определения положения фронта через промежуток времени D t надо каждую точку фронта рассматривать как вторичный источник сферической волны. Поверхность, огибающая вторичные сферические волны радиусом с D t, представляет фронт волны через промежуток времени D t. Но Гюйгенс не учитывал эффекты интерференции. С учетом явления интерференции вторичных волн данный принцип носит название принципа Гюйгенса–Френеля. При анализе распространения волн необходимо учитывать фазу и амплитуду интерферирующих вторичных волн (подробнее о принципе Гюйгенса-Френеля будет изложено в главе 7).
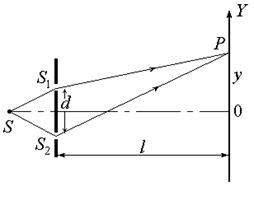 Рис. 5.3
Рис. 5.3
|
Опыт Юнга. (1801 г.) Рассмотрим интерференцию, возникающую в результате выделения с помощью двух щелей S 1и S 2 участков сферического волнового фронта волны от точечного источника S (рис.5.3) (метод деления волнового фронта). Найдем разность хода лучей в произвольной точке наблюдения P на экране:
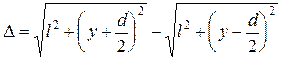 . (5.12)
. (5.12)
При 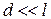 (что обычно реализуется в эксперименте) получаем:
(что обычно реализуется в эксперименте) получаем:
 . (5.13)
. (5.13)
Следовательно, с точностью до величины первого порядка по 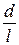 имеем:
имеем:
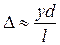 . (5.14)
. (5.14)
Разность фаз между волнами в точке наблюдения при этом равна:
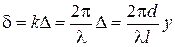 . (5.15)
. (5.15)
Интерференционная картина на экране в зависимости от координаты y принимает вид:
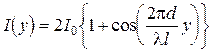 (5.16)
(5.16)
Расстояние на экране наблюдения между соседними максимумами или минимумами интенсивности называется шириной интерференционной полосы. Для схемы Юнга ширина полосы определяется по формуле:
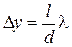 (5.17)
(5.17)
и не зависит от порядка интерференции, являясь постоянной при заданных l, d и l. Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.
Примеры экспериментальных интерференционных схем, осуществляющих метод деления волнового фронта: бипризма Френеля, билинза Бийе, бизеркало Френеля, зеркало Ллойда.
Интерференция при белом свете. Каждая волна со своей длиной в данной схеме создает свою систему интерференционных полос, причем центральный максимум (при y = 0) имеет вид белой полосы, т.к. он совпадает для всех длин волн. Первые минимумы (первые темные полосы) для всех длин волн очень близки и не перекрываются с полосами высших порядков. Следующие интерференционные полосы окрашены, т.к. эти максимумы для разных длин волн разнесены в пространстве (в данном случае по y). При дальнейшем увеличении порядка интерференции интерференционная картина постепенно пропадает, т.к. дальние полосы накладываются друг на друга и смазываются.
 Рис. 5.4
Рис. 5.4
|
Временная и пространственная когерентность. Необходимое условие существования интерференции можно сформировать в следующем виде: для возникновения интерференции необходимо, чтобы разность фаз между интерферирующими волнами (см. (5.4)) сохраняла свое значение за время усреднения. Поэтому и вводят понятие когерентных колебаний, для которых разность фаз за время наблюдения остается неизменной. При описании интерференционных явлений часто используют понятия временной и пространственнойкогерентности. Временную когерентность обычно связывают со степенью монохроматичности волн (например, в интерферометре Майкельсона при рассмотрении осевых пучков), а пространственную когерентность – с геометрией эксперимента (как в опыте Юнга или при рассмотрении интерференции от протяженных источников света).
Рассмотрим условие возникновения интерференции с более общих позиций. Пусть две волны одинаковой частоты w, распространяющиеся от точечных источников О 1 и О 2, достигают точку наблюдения Р через различные интервалы времени t 1 и t 2 (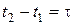 ) (рис.5.4). Тогда
) (рис.5.4). Тогда
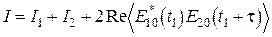 . (5.18)
. (5.18)
Функция 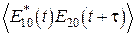 называется функцией корреляции (
называется функцией корреляции (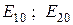 – комплексные в общем случае амплитуды). Чаще употребима нормированная функция корреляции
– комплексные в общем случае амплитуды). Чаще употребима нормированная функция корреляции
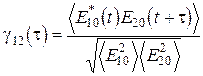 . (5.19)
. (5.19)
Эта функция определяет комплексную (в общем случае) степень когерентности исследуемых волн. Ее свойство: если произведение амплитуд волн за время t, много большее по сравнению с периодом колебаний, совершает хотя бы одно изменение знака, то она при t®¥ стремится к нулю, если нет – то к единице. Т.о. эта функция показывает степень сфазированности двух волн с одинаковой частотой за временной отрезок t. При различных частотах смысл функции корреляции несколько иной и мы его затрагивать здесь не будем.
Пусть в интерферометре Майкельсона мы делим одну волну на две с временной задержкой t. Тогда функция 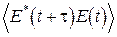 называется функцией автокорреляции. Ее нормированная форма имеет вид
называется функцией автокорреляции. Ее нормированная форма имеет вид
 . (5.20)
. (5.20)
Пользуясь понятием функции корреляции, соотношение (5.5) можно записать в виде:
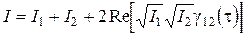 (5.21)
(5.21)
На практике для количественной характеристики качества интерференционной картины вводят понятие ее функции видности:
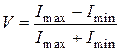 , (5.22)
, (5.22)
где 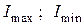 – экспериментально определяемые величины в точке наблюдения:
– экспериментально определяемые величины в точке наблюдения:
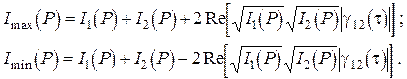 (5.23)
(5.23)
Если 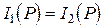 , то
, то 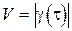 . Т.е. в этом случае модуль функции автокорреляции и определяет видность интерференционной картины.
. Т.е. в этом случае модуль функции автокорреляции и определяет видность интерференционной картины.
Допустим, что наша волна имеет следующую временную зависимость (рис.5.5):
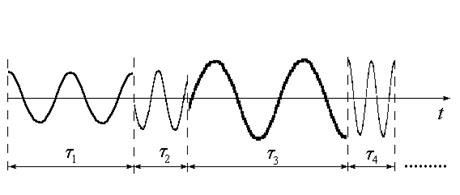 Рис. 5.5
Рис. 5.5
|
ti – средние времена смены фазы колебания амплитуды. Величина
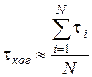 (5.24)
(5.24)
является характерным временным масштабом случайных флуктуаций фазы световой волны и называется временем когерентности. Путь, проходимый волной за время когерентности, называется длиной когерентности:
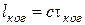 . (5.25)
. (5.25)
Размывание полос интерференции в интерферометре Майкельсона обусловлено конечностью времени и длины когерентности света, т.е. обусловлено временной когерентностью.
При рассмотрении пространственной когерентности функция 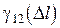 характеризует также интерференционное качество волны, т.е. способность различных участков волнового фронта к взаимной когерентности. В этом случае D l – расстояние между соответствующими точками на волновом фронте.
характеризует также интерференционное качество волны, т.е. способность различных участков волнового фронта к взаимной когерентности. В этом случае D l – расстояние между соответствующими точками на волновом фронте.
 Рис.5.6
Рис.5.6
|
Оценим максимальные размеры источника, при котором интерференция еще наблюдается, т.е. пространственная когерентность сохраняется. Пусть задан протяженный источник света с шириной b (рис.5.6). 2j – угловая апертура интерференции. В направлении 1 положение каждой точки в пределах b роли не играет. При распространении под углом к этому направлению положение каждого точечного источника обуславливает дополнительную разность хода. Максимальная разность хода достигается между направлениями 1 и 2 или 1 и 3:
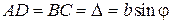 . (5.26)
. (5.26)
При 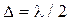 интерференционная картина исчезает. При уменьшении значения
интерференционная картина исчезает. При уменьшении значения 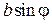 наблюдаются размытые интерференционные полосы (частичная когерентность). Интерференционная картина становится достаточно четкой, если смещение интерференционных картин, полученных от крайних точек A и B протяженного источника, не превышает половины полосы, т.е.
наблюдаются размытые интерференционные полосы (частичная когерентность). Интерференционная картина становится достаточно четкой, если смещение интерференционных картин, полученных от крайних точек A и B протяженного источника, не превышает половины полосы, т.е.
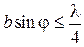 . (5.27)
. (5.27)
Это соотношение, связывающее апертуру интерференции и размеры протяженного источника, называется условием пространственной когерентности. При дальнейшем уменьшении размеров источника его можно считать практически точечным.
Перейдем к более подробному рассмотрению интерференции, получаемой по методу деления амплитуд. При изучении общей теории интерференционных схем необходимо отметить, что происхождение интерференционной картины и способ ее получения определяют вид интерференционных полос. Пусть интерференционное устройство представляет собой слой прозрачного диэлектрика с частично отражающими и пропускающими поверхностями, в котором возникает геометрическая разность хода D при произвольном угле падения j света на это устройство. К такому типу интерферометров можно отнести плоскопараллельные и клиновидные диэлектрические пластины (например, интерференция в тонких пленках, кольца Ньютона и др.), а также интерферометры, расщепляющие пучки с помощью зеркал (интерферометр Майкельсона и его аналоги, эталон (!) Фабри-Перо). Здесь можно рассмотреть три вида интерференционных полос, получающихся при следующих условиях:
1. l = const; j = const. При вариации геометрической разности хода имеют место полосы равной толщины.
2. l = const; D = const. При вариации угла падения получаем полосы равного наклона.
3. j = const; D = const. При вариации длины волны получаем полосы равного хроматического порядка.
Полосы равной толщины возникают в том случае, если интерферирующие пучки после прохождения интерференционной системы имеют реальное или мнимое пересечение в пространстве изображений.
Полосы равного наклона возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.
Полосы равного хроматического порядка здесь мы рассматривать не будем, т.к. этот случай в обычных интерференционных схемах используется крайне редко (для очень точных измерений толщины плоскопараллельных пластин или воздушных промежутков).
Интерференция в тонких пленках. При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина волны, т.к. ее частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления:
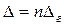 . (5.28)
. (5.28)
Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме.
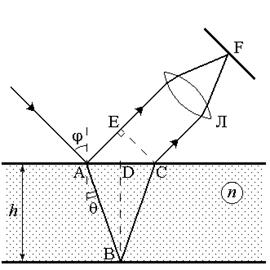 Рис.5.7
Рис.5.7
|
а) Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом j на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h (рис.5.7). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности или в фокальной плоскости F линзы Л. С учетом потери полволны на границе раздела сред (если n > 1, то в точке A, если n < 1, то в точке B) оптическая разность хода в данном случае равна
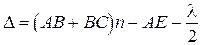 . (5.29)
. (5.29)
Из геометрии рисунка (вывести самостоятельно!) получаем для оптической разности хода:
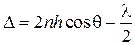 . (5.30)
. (5.30)
Условием максимума интерференционной картины по-прежнему является
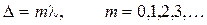 . (5.31)
. (5.31)
а условием минимума –
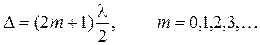 (5.32)
(5.32)
Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями.
Даже если источник света протяженный и различные его точки излучают некогерентно, то интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка A на рис. 5.7) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором.
Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии). Немонохроматичность ухудшает видность интерференционной картины. С другой стороны, увеличение толщины пластины уменьшает дисперсионную область. Для наблюдения интерференции в белом свете толщина должна быть достаточно малой (~ 10 мкм). Поэтому в данном случае речь идет об интерференции в тонких пленках.
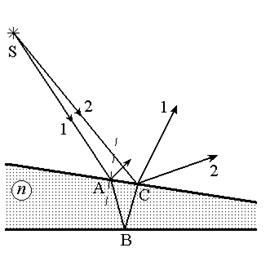 Рис.5.8
Рис.5.8
|
б) Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.5.8). В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке C и высчитывается по той же формуле, что и (5.30). Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Ограничения на толщину клиновидной пластины, связанные со степенью временной когерентности (или монохроматичности) такие же, как и в случае плоскопараллельной пластины.
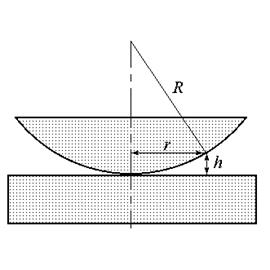 Рис.5.9
Рис.5.9
|
Кольца Ньютона. Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот) (рис.5.9). В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина. Пусть h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы. Найдем радиус темного интерференционного кольца m -го порядка. Из геометрии рисунка видно, что  . Учитывая, что
. Учитывая, что  , получаем
, получаем 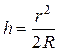 . Используя условие минимума (5.32), получаем для радиуса m -го темного кольца:
. Используя условие минимума (5.32), получаем для радиуса m -го темного кольца:
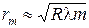 . (5.33)
. (5.33)
Интерференционные кольца наблюдаются как в отраженном, так и в прошедшем свете. При этом там, где в отраженном свете наблюдается светлое кольцо, то в прошедшем – темное, т.е. интерференционные картины в прошедшем и отраженном свете являются взаимно дополнительными. Центральное пятно в отраженном свете – темное, т.к. толщина воздушного клина пренебрежительно мала и волны интерферируют практически в противофазе из-за потери полволны. В белом свете, как и следует из формулы (5.33), наблюдаются цветные кольца.
Контрастность интерференционных картин в отраженном и прошедшем свете неодинакова. Для наблюдения четкой интерференционной картины в отраженном свете поверхности клина должны обладать малым коэффициентом отражения, а в прошедшем – большим. Это легко видеть из соотношений амплитуд интерферирующих волн, которые для лучшей видимости должны стремиться к единице. Для отраженных волн оно равно 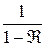 , а для прошедших –
, а для прошедших – 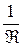 , где Â – энергетический коэффициент отражения (проверить самостоятельно).
, где Â – энергетический коэффициент отражения (проверить самостоятельно).

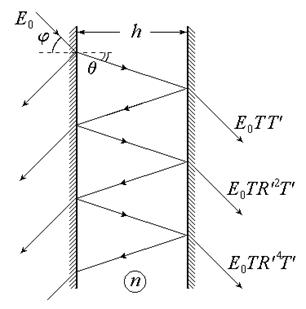 Рис. 5.10
Рис. 5.10
|
Многолучевая интерференция. До сих пор мы рассматривали интерференцию между двумя волнами. Теперь рассмотрим многолучевую интерференцию на примере интерферометра Фабри–Перо (ИФП) (рис.5.10). Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим 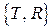 – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,
– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины, 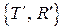 – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
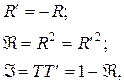 (5.34)
(5.34)
где Á и Â – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения j и преломления q достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода D между соседними интерферирующими волнами на выходе пластины равна
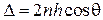 , (5.35)
, (5.35)
а разность фаз равна
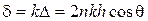 . (5.36)
. (5.36)
Запаздывание последующей волны относительно предыдущей за счет прохождения волны в пластинке учтем множителем е- id. Суммарная амплитуда E 2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
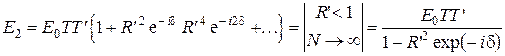 . (5.37)
. (5.37)
Интенсивность света определяется следующим образом:
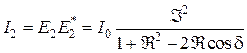 или
или
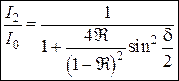 . (5.38)
. (5.38)
Эта формула носит название формулы Эйри.
Отметим, что аналогично можно найти суммарную интенсивность света при отражении от плоскопараллельной пластинки:
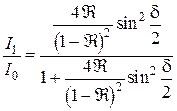 . (5.39)
. (5.39)
Интерференционные картины в проходящем и отраженном свете оказываются дополнительными.
Вид функции Эйри (5.38) для трех различных коэффициентов отражения (1 – Â =0, 04; 2 – Â =0, 4; 3 – Â =0, 8) представлен на рис.5.11. Максимумы функции 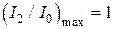 достигаются при
достигаются при 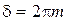 , где m = 0, 1, 2,..., а минимумы
, где m = 0, 1, 2,..., а минимумы 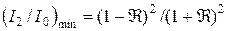 – при
– при 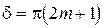 . Т.о. функция видности интерференционной картины равна:
. Т.о. функция видности интерференционной картины равна:
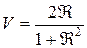 , (5.40)
, (5.40)
т.е. при Â ® 1 Þ V ® 1. При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
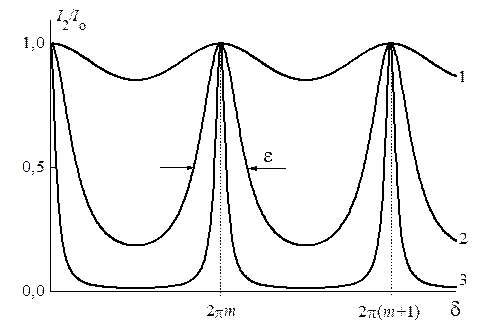 Рис. 5.11
Рис. 5.11
|
Если на ИФП падают пучки света под всевозможными углами, то интерференционные полосы имеют вид колец. Максимальный порядок интерференции соответствует центру интерференционной картины. Интерференционная картина имеет одинаковый вид там, где падающие пучки имеют одинаковый угол падения на ИФП (полосы равного наклона). Интерференционная картина наблюдается или на бесконечности, или (что обычно реализуется в эксперименте) в фокальной плоскости линзы.
В реальных измерительных ИФП интерференция возникает между двумя отполированными с высокой точностью (~0, 01l) плоскими строго параллельными (с плоскостностью до 0, 005) зеркалами с большими коэффициентами отражения (алюминиевые зеркала – ~75%, посеребренные – ~90%, диэлектрические интерференционные – до 99, 9%). Интерферометр с показателем преломления между зеркалами n = 1 называется эталоном Фабри–Перо).