
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы расчета магнитной цепи
|
|
При расчете магнитной цепи могут быть две задачи: прямая, когда известны геометрические размеры и магнитные свойства материала магнитопровода, а также значение магнитного потока Ф (определяются магнитодвижущая сила и ток I в витках обмотки), и обратная, когда задается магнитодвижущая сила, геометрические размеры и материалы магнитопровода (определяется магнитный поток Ф).
Рассмотрим прямую задачу. В неразветвленной и неоднородной магнитной цепи (см. рис. 3, б) известны: значение магнитного потока в воздушном зазоре Ф, геометрические размеры и материал магнитопровода, число витков обмотки w, а также зависимость Вм(Н) (рис. 8, б). Определить мдс wI.
ПРИМЕР Алгоритм расчета магнитной цепи можно представить в следующем виде:
1. По заданным геометрическим размерам определяем Sм; Sв; lм и lв.
2. По заданному магнитному потоку Ф определяем магнитные индукции Вм, Вв на участках магнитной цепи.
Цепь одноконтурная, следовательно, магнитный поток Ф во всех участках цепи будет неизменным. Полагая Sв = Sм получим

3. По вычисленным Вм и кривой намагничивания В(Н) для заданного материала магнитопровода находим Нм (рис. 8, б).
4. Обходя контур в направлении магнитного потока, запишем уравнение магнитного состояния
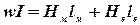

здесь 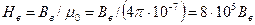 — напряженность магнитного поля в воздушном зазоре.
— напряженность магнитного поля в воздушном зазоре.
Таким образом, расчетное уравнение примет вид 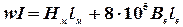
В обратной задаче расчета магнитной цепи задается мдс wI и требуется определить магнитный поток Ф на участке цепи (или в воздушном зазоре).
Из-за нелинейности зависимость Ф (wI) необходимо предварительно рассчитать и построить, а затем для заданного значения wI определить Фв. Для построения зависимости Ф(wI) задают 5—7 значений магнитного потока, по алгоритму «прямой задачи» рассчитывают соответствующие значения мдс и строят зависимости Ф(wI).
Во многих электротехнических устройствах (электрических машинах, трансформаторах и др.) используют симметричные магнитные системы (см. рис. 3, в). В цепи такой системы магнитный поток Ф1 равен потоку Ф2. В среднем сердечнике магнитопровода оба потока Ф1 и Ф2 складываются, но и сечение сердечника вдвое больше сечения крайних сердечников. При расчете такую цепь можно представить как две самостоятельные, если мысленно разделить магнитопровод по вертикальной оси ab. Магнитные потоки Ф1 и Ф2 при таком делении останутся неизменными по направлению. Иными словами, схему замещения магнитной цепи такой магнитной системы можно представить двумя независимыми неразветвленными магнитными цепями, в которых действуют одинаковые мдс, и рассчитывать одну из двух составляющих. При решении прямой задачи, когда задан магнитный поток Ф в любом стержне, полученное значение мдс равно значению полной мдс. При решении обратной задачи значение магнитного потока в среднем стержне Ф1 определяют на основании уравнения состояния узла.