
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионный анализ. При исследовании взаимосвязей между выборками помимо корреляции различают также и регрессию
|
|
При исследовании взаимосвязей между выборками помимо корреляции различают также и регрессию. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. Соответственно, наряду с корреляционным анализом еще одним инструментом изучения стохастических зависимостей является регрессионный анализ.
Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.
В линейном регрессионном анализе связь между случайными величинами предполагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные X и Y. И требуется по п парам наблюдений (Х1, Y1), (Х2, Y2), ..., (Хп, Yn) построить (подобрать) прямую линию, называемую линией регрессии, которая «наилучшим образом» приближает наблюдаемые значения. Уравнение этой линии Y = аХ + b является регрессионным уравнением. С помощью регрессионного уравнения можно предсказать ожидаемое значение зависимой величины Y0, соответствующее заданному значению независимой переменной Хо.
Таким образом, можно сказать, что линейный регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений. В регрессионном анализе все признаки (переменные), входящие в уравнение, должны иметь непрерывную, а не дискретную природу.
В случае, когда рассматривается зависимость между одной зависимой переменной Y и несколькими независимыми Х1, Х2,..., Хn, говорят о множественной линейной регрессии. В этом случае регрессионное уравнение имеет вид
Y = ао + а1Х1 + а2Х2 +... + апХп,
где а1, а2,..., аn — требующие определения коэффициенты при независимых переменных X1, Х2,..., Хп; а0 — константа.
Мерой эффективности регрессионной модели является коэффициент детерминации R2 (R-квадрат). Коэффициент детерминации (R-квадрат) определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксимирует) исходные данные.
Исследуется также значимость регрессионной модели с помощью F- критерия (Фишера). Если величина F-критерия значима (р < 0, 05), то регрессионная модель является значимой.
Достоверность отличия коэффициентов а0, а1, а2..., аn от нуля проверяется с помощью критерия Стьюдента. В случаях, когда р > 0, 05, коэффициент может считаться нулевым, а это означает, что влияние соответствующей независимой переменной на зависимую переменную недостоверно, и эта независимая переменная может быть исключена из уравнения.
В MS Excel экспериментальные данные аппроксимируются линейным уравнением до 16 порядка:
Y= а0 + а1Х1 + а2Х2 +... + а16X16,
где Y — зависимая переменная, Х1, ..., Х16 — независимые переменные, а0, а1, ..., а16 — искомые коэффициенты регрессии.
Для получения коэффициентов регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ для получения предсказанных значений Y в требуемых точках (см. раздел «Несколько независимых переменных» главы 3).
Для реализации процедуры Регрессия необходимо:
О выполнить команду Сервис ► Анализ данных;
О в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку 0К;
О в появившемся диалоговом окне задать Входной интервал Y, то есть ввести ссылку на диапазон анализируемых зависимых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку столбца зависимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
О указать Входной интервал X, то есть ввести ссылку на диапазон независимых данных, содержащий до 16 столбцов анализируемых данных. Для этого следует навести указатель мыши на поле ввода Входной интервал X и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю левую ячейку диапазона независимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
О указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши (рис. 6.23). Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;
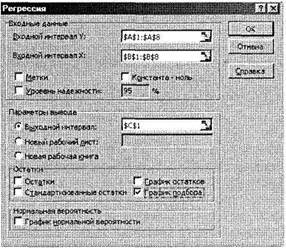
Рис. 6.23. Пример заполнения диалогового окна Регрессия
О если необходимо визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора;
О нажать кнопку ОК.
Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.
Интерпретация результатов. Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
О Y -пересечение — а0;
О переменная XI — а1;
О переменная Х2 — а2 и т. д.
В столбце Р-Значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда Р > 0, 05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
Приводимое значение R-квадрат (коэффициент детерминации) определяет, с какой степенью точности полученное регрессионное уравнение аппроксимирует исходные данные. Если R-квадрат > 0, 95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0, 8 до 0, 95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0, 6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
Пример 6.15. В отделе снабжения гостиницы имеется информация об изменении стоимости стирального порошка за длительный период времени. Сопоставляя его с изменениями курса доллара за этот же период времени, можно построить регрессионное уравнение. Ниже приведены стоимость пачки стирального порошка (в руб.) и соответствующий курс доллара (pyб./USD).
| N | Порошок | Курс |
| 6, 3 | ||
| 29, 3 |
Необходимо на основании этих данных построить регрессионное уравнение, позволяющее по курсу доллара определять предполагаемую стоимость пачки стирального порошка.