
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткая теория. Цель работы:получить экспериментальную зависимость сопротивления полупроводника от температуры и по ней рассчитать ширину запрещенной зоны (энергию активации)
|
|
Лабораторная работа № 3
ОПРЕДЕЛЕНИЕ ШИРИНЫ
ЗАПРЕЩЕННОЙ ЗОНЫ ПОЛУПРОВОДНИКОВ
Цель работы: получить экспериментальную зависимость сопротивления полупроводника от температуры и по ней рассчитать ширину запрещенной зоны (энергию активации) и температурный коэффициент сопротивления.
Приборы и принадлежности: 1.Терморезистор. 2. Электронагреватель. 3. Термометр.
4. Мост одинарный РЗЗЗ. 5. Источник тока. 6. ЛАТР. 7. Соединительные провода.
Краткая теория
Изолированный атом имеет определенные значения энергии. В кристаллической решетке, состоящей из N таких атомов, каждый уровень энергии расщепляется на N квантовых состояний, которые составляют энергетическую зону. Поскольку соседние уровни энергии в зоне различаются па величину порядка
10-22 — 10-23 эВ, то зону разрешенных дискретных значений можно рассматривать как квазинепрерывную энергетическую зону.
Чтобы участвовать в процессе проводимости, электрон, получая дополнительную энергию за счет электрического поля, должен переходить на свободный высокий уровень энергии. Однако, если все уровни в зоне
заняты электронами, то переход электрона на более высокие уровни энергии в пределах энергетической зоны невозможен. В зависимости от того, частично или полностью заполнена электронами высшая энергетическая (валентная) зона, твердое тело ведет себя либо как металл, либо как диэлектрик.
Электрическая зона, образованная уровнями валентных электронов атомов, называется валентной зоной. Следующая зона разрешенных значений энергии, свободная от электронов при абсолютном нуле температуры, называется зоной проводимости (или свободной зоной). Валентная зона отделена от зоны проводимости полосой запрещенных для электрона значений энергий — запрещенной зоной
(рис. 1.1, левая часть).
При температуре выше абсолютного нуля некоторая часть электронов валентной зоны вследствие теплового возбуждения может получить энергию, достаточную для их перехода из валентной зоны в зону проводимости (см. рис. 1.1). Эта энергия называется энергией активации и равна она ширине запрещенной зоны 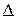 Е. В результате такого перехода в зоне проводимости появится некоторое число электронов, которые участвуют в создании электрического тока. Одновременно в валентной зоне образуются свободные квантовые состояния, благодаря чему валентная зона тоже участвует в создании электрического тока.
Е. В результате такого перехода в зоне проводимости появится некоторое число электронов, которые участвуют в создании электрического тока. Одновременно в валентной зоне образуются свободные квантовые состояния, благодаря чему валентная зона тоже участвует в создании электрического тока.
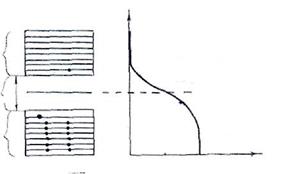
| зона проводимости запрещенная зона валентная зона |
|
| Е |
 ЕF ЕF
|
| f(Е) |
| 0 0, 5 1 |
Перемещение электрона валентной зоны под действием электрического поля эквивалентно перемещению положительного заряда той же величины в противоположном направлении. Механизм перемещения электронов в валентной зоне выглядит так.
Рис. 1.1
Под действием электрического поля электроны разрывают свои ковалентные связи и заполняют вакантные места (дырки) в зоне. Однако на месте разрывов ковалентных связей образуются немые дырки. Таким образом, электроны перемещаются в направлении, противоположном направлению вектора напряженности электрического поля, а дырки — в направлении этого вектора. Дырки можно рассматривать как квазичастицы (нереальные частицы), являющиеся носителями положительного электрического заряда. Поэтому электропроводность кристалла слагается из электродной и дырочной составляющих электропроводности.
Величина электропроводности пропорциональна концентрации свободных носителей (электронов и дырок), а распределение электронов по уровням валентной зоны и зоны проводимости описывается функцией Ферми—Дирака
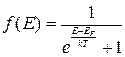 (1.1)
(1.1)
где Е – энергия электрона;
ЕF – уровень Ферми;
k= 1, 38∙ 10-23 Дж/К=8, 62∙ 10 5 эВ/К – постоянная Больцмана;
Т – абсолютная температура;
f(E) – вероятность того, что уровень с энергией Е занят электронами.
Это распределение можно сделать очень наглядным, изобразив, как это сделано на рис. 1.1, график функции распределения совместно со схемой энергетических зон. Расчеты показывают, что значение уровня Ферми, отсчитанное от потолка валентной зоны, приблизительно равно
 (1. 2)
(1. 2)
где 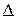 Е – ширина запрещенной зоны. Это означает, что уровень Ферми лежит посредине
Е – ширина запрещенной зоны. Это означает, что уровень Ферми лежит посредине
запрещенной зоны.
Пусть энергия электронов в зоне проводимости равна Е. Тогда разность
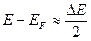 (1.3)
(1.3)
При температурах, отличных от абсолютного нуля, в случае больших значений (т. е. при 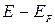 > > kT) единицей в знаменателе функции (1.1) можно пренебречь. Тогда распределение электронов по состояниям с различной энергией принимает вид
> > kT) единицей в знаменателе функции (1.1) можно пренебречь. Тогда распределение электронов по состояниям с различной энергией принимает вид
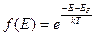
на основании выражения (1.3) запишем
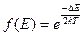 (1.4)
(1.4)
т. е. распределение Ферми — Дирака переходит в функцию распределения Больцмана.
Число электронов, перешедших в зону проводимости, а следовательно, и число образовавшихся дырок, будет пропорционально вероятности (1.4). Эти электроны и дырки являются носителями заряда и создают ток. Поскольку проводимость пропорциональна концентрации носителей заряда, то она пропорциональна вероятности f(E). Поэтому электропроводность σ полупроводников быстро растет с температурой, изменяясь по закону
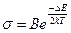
где В — константа.
Следовательно, сопротивление полупроводника при нагревании будет уменьшаться по экспоненте
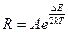 (1.5)
(1.5)
где A – коэффициент, зависящий от физических свойств полупроводника. При Т 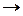
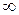 A
A  R. Прологарифмируем выражение (1.5):
R. Прологарифмируем выражение (1.5):
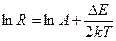 (1.6)
(1.6)
График зависимости InR от 1/Tдля собственных полупроводников представляет собой прямую линию (рис. 1.2), тангенс угла наклона которой к оси абсцисс равен

 lnR
lnR
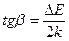
 |
Для двух различных температур Т1 и Т2 выражение (1.6) запишется так:
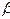
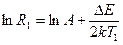
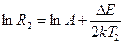

отсюда
| Рис. 1.2 |
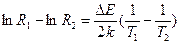
В окончательном виде расчетная формула запишется
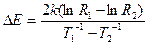 (1.7)
(1.7)
Температурный коэффициент сопротивления α показывает, на сколько изменяется единица сопротивления при нагревании на один градус, т. е.
 (1.8)
(1.8)
Воспользуемся выражением (1.5) и найдем
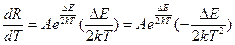
Полученный результат подставим в выражение (1.8):

Окончательная расчетная формула для определения температурного коэффициента сопротивления будет
 (1.9)
(1.9)
Из формулы (1.9) следует, что в отличие от металлов коэффициент сопротивления полупроводников не является постоянным и значительно зависит от температуры (у металлов а≈ 1/273 К-1). Знак минус в формуле (1.9) показывает, что у полупроводников сопротивление при повышении температуры уменьшается.