
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции непрерывной случайной величины
|
|
Функции случайных величин
Функции дискретной случайной величины
Если аргумент X принимает значения 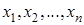 с вероятностями
с вероятностями 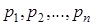 , тогда функция Y = f(x) примет соответствующие значения
, тогда функция Y = f(x) примет соответствующие значения 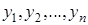 по некоторому правилу y = f(x) с теми же вероятностями
по некоторому правилу y = f(x) с теми же вероятностями 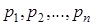 .
.
Пример. Указан ряд распределения случайной величины:
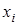
| – 3 | – 2 | – 1 | ||||
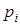
| 0, 1 | 0, 1 | 0, 2 | 0, 2 | 0, 2 | 0, 1 | 0, 1 |
Значения 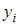 находим по формуле
находим по формуле 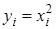 :
:
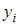
| |||||||
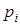
| 0, 1 | 0, 1 | 0, 2 | 0, 2 | 0, 2 | 0, 1 | 0, 1 |
Составим ряд распределения случайной величины 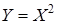 . Поскольку разным значениям
. Поскольку разным значениям 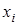 соответствуют одинаковые значения
соответствуют одинаковые значения 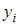 , объединим их, указав в таблице суммарную вероятность:
, объединим их, указав в таблице суммарную вероятность:
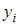
| ||||
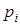
| 0, 2 | 0, 4 | 0, 2 | 0, 2 |
Функции непрерывной случайной величины
Пусть непрерывная случайная величина X, принимающая значения на промежутке 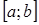 , с плотностью распределения р(х) и другая случайная величина Y связаны функциональной зависимостью Y = f(x). Найти промежуток
, с плотностью распределения р(х) и другая случайная величина Y связаны функциональной зависимостью Y = f(x). Найти промежуток 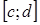 , на котором принимает свои значения Y, и плотность распределения Y
, на котором принимает свои значения Y, и плотность распределения Y 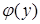 .
.
Пусть р(х) и f(x) – непрерывные функции, причем f(x) – возрастающая на 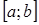 функция. Каждому значению х случайной величины Х соответствует определенное значение y случайной величины Y. Изменению Х от х до x + dx отвечает изменение Y от y до y + dy, поэтому вероятности попадания на эти промежутки одинаковы:
функция. Каждому значению х случайной величины Х соответствует определенное значение y случайной величины Y. Изменению Х от х до x + dx отвечает изменение Y от y до y + dy, поэтому вероятности попадания на эти промежутки одинаковы: 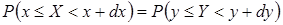 . Используя функции плотности распределения, предыдущее равенство можно записать так:
. Используя функции плотности распределения, предыдущее равенство можно записать так:  . Откуда следует:
. Откуда следует: 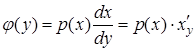 .
.
Если же на промежутке 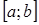 f(x) – убывающая функция, то
f(x) – убывающая функция, то 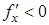 . Т.к. производная прямой и обратной функции связаны соотношением
. Т.к. производная прямой и обратной функции связаны соотношением 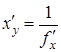 , то
, то 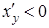 . Поскольку
. Поскольку 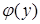 по определению неотрицательная функция, то, чтобы найти
по определению неотрицательная функция, то, чтобы найти 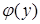 , нужно использовать следующую формулу:
, нужно использовать следующую формулу: 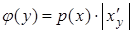 .
.
В том случае, если на 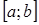 имеется несколько промежутков возрастания и убывания, то нужно найти плотность распределения
имеется несколько промежутков возрастания и убывания, то нужно найти плотность распределения 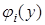 на каждом участке. Сумма полученных функций даст искомую плотность распределения:
на каждом участке. Сумма полученных функций даст искомую плотность распределения:
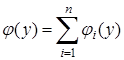 ,
,
где n – число промежутков строго монотонного изменения функции f(x).
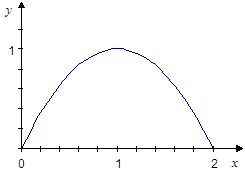 Пример. Случайная величина Х принимает значения на промежутке
Пример. Случайная величина Х принимает значения на промежутке 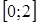 с плотностью
с плотностью  . Найти промежуток изменения и плотность распределения
. Найти промежуток изменения и плотность распределения 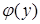 случайной величины
случайной величины 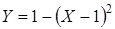 . Построив график функции
. Построив график функции 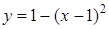 на промежутке
на промежутке 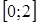 , найдем, что
, найдем, что 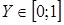 .
.
Из графика видно, что на промежутке 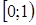 функция
функция 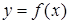 возрастает, а на промежутке
возрастает, а на промежутке 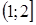 убывает. Найдем вид функции
убывает. Найдем вид функции 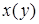 :
: 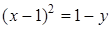 , откуда
, откуда 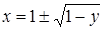 . Если
. Если 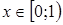 , то
, то 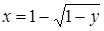 ; если
; если 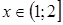 , то
, то 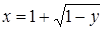 . Определим
. Определим 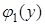 :
:
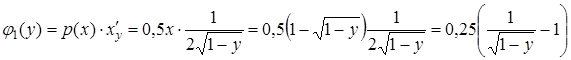 .
.
Теперь найдем 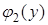 :
:
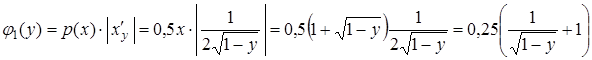 .
.
Следовательно, 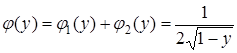 . Сделаем проверку:
. Сделаем проверку:
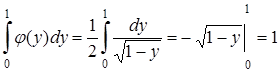 .
.
|