Предварительные сведения.

Множество G с заданной на нём бинарной операцией «*»: 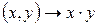, называется группой, если выполнены следующие аксиомы:

1. Операция ассоциативна: 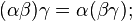для всех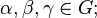

2. G обладает нейтральным элементом : 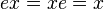для всех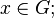

3. Для каждого элемента 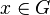существует обратный :

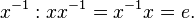
порядок группы. Группа с коммутативной операцией называется коммутативной, а чаще – абелевой. Подмножество 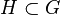называется подгруппой в G, если 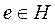, 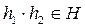для любых 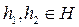, 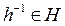(обозначение ).

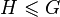Обозначим через группу, порождённую элементами 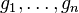, т.е. каждый элемент 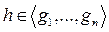представляется в виде 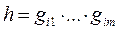для некоторого натурального 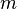. Группа G называется циклической, если 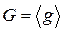для некоторого .

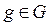Подгруппа N группы G называется нормальной, если она инвариантна относительно сопряжений, то есть для любого элемента n из N и любого g из G, элемент лежит в N:

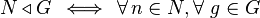
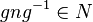
Следующие условия нормальности подгруппы эквивалентны:

1. Для любого g из G, .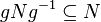

2. Для любого g из G, .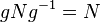

3. Множества левых и правых смежных классов N в G совпадают.

4. Для любого g из G, .

5. N изоморфна объединению классов сопряженных элементов.

Симметрической группой множества G называется группа всех перестановок G (то есть биекций 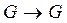) относительно операции композиции.

Симметрическая группа множества G обычно обозначается S (G). Если 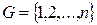, то S (G) также обозначается через S_n. Но если , то S (G) изоморфна S (Y), потому при конечном 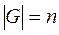считают, что S (G) равно S_n.

Нейтральным элементом в симметрической группе является тождественная перестановка id, определяемая как тождественное отображение:

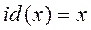для всех .

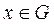Подгруппа симметрической группы S (G) называется группой перестановок G.

Знакопеременной группой перестановок степени n (обозн. A_n) называется подгруппа симметрической группы S_n степени n, содержащая только чётные перестановки.

Коммутант группы G — подгруппа, порождённая множеством 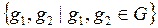всевозможных произведений конечного числа коммутаторов пар элементов группы G. Используются следующие обозначения для коммутанта группы G: , , 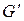T₂ (G), K (G). При этом коммутаторы могут записываться по-разному: или .

Любая подгруппа, содержащая коммутант, является нормальной.

Подмножество называется орбитой элемента .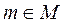

Действие группы G на множестве M определяет на нём отношение эквивалентности: .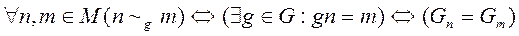

При этом классами эквивалентности являются орбиты элементов.

Подмножество 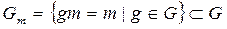является подгруппой группы G и называется стабилизатором или стационарной подгруппой элемента .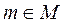