
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параметры Эйлера
|
|
Теорема Эйлера утверждает, что угловая ориентация любой системы координат 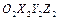 может быть совмещена с угловой ориентацией любой другой системы координат
может быть совмещена с угловой ориентацией любой другой системы координат 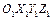 поворотом вокруг единичного вектора
поворотом вокруг единичного вектора  на некоторый угол, при этом координаты вектора
на некоторый угол, при этом координаты вектора  в обеих системах координат совпадают.
в обеих системах координат совпадают.
Как и ранее будем рассматривать только правые системы координат. Будем также считать, что положительное значение угла поворота соответствует повороту по правилу правого винта (правилу «буравчика»).
Обозначим
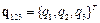 ;
;
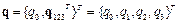 .
.
Параметры Эйлера определяются следующими выражениями
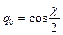 ; (1)
; (1)
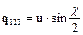 , (2)
, (2)
где 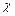 - угол поворота;
- угол поворота;  - единичный вектор, вокруг которого производится поворот,
- единичный вектор, вокруг которого производится поворот,  .
.
Параметры Эйлера также принято называть кватернионом. В отличие от трехкратных поворотов параметры Эйлера не имеют особых точек, и поэтому они часто используются для описания ориентации систем координат. Отметим некоторые свойства параметров Эйлера.
Свойство 1. Сумма квадратов параметров Эйлера равна единице.
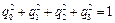 . (3)
. (3)
Свойство 2. Одновременное изменение знаков всех параметров Эйлера не изменяет ориентацию системы координат.
Примем, что параметры Эйлера определяют поворот 2-й системы координат относительно 1-й системы координат при их первоначальном совпадении. В этом случае матрица поворота имеет следующий вид
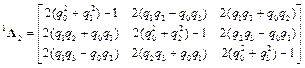 . (4)
. (4)
Предположим, что известны значения элементов матрицы поворота
 .
.
Тогда из (4) можно определить значения параметров Эйлера. Используя свойство 1 можно получить следующее выражение для суммы элементов на главной диагонали
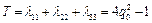 .
.
Отсюда получаем
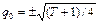 .
.
В соответствии со свойством 2 можно взять как положительное так и отрицательное значение  . Если
. Если 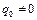 , тогда
, тогда
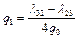 ,
, 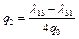 ,
, 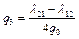 ,
,
в противном случае выбирается наибольший элемент на главной диагонали. В соответствии со свойствами матрицы поворота его значение больше минус единица. Предположим это 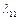 , тогда
, тогда
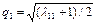 ,
, 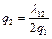 ,
, 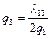 .
.
Продифференцировав (3) получаем следующее соотношение
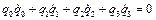 . (5)
. (5)
Из выражения для угловой скорости  с учетом (5) получаем следующее соотношение для вектора угловой скорости
с учетом (5) получаем следующее соотношение для вектора угловой скорости
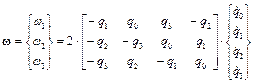 . (6)
. (6)
Из выражения для углового ускорения 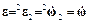 получаем следующее соотношение для вектора углового ускорения
получаем следующее соотношение для вектора углового ускорения
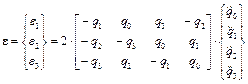 . (7)
. (7)
Из соотношения (7) следует, что для параметров Эйлера в общем выражении для углового ускорения 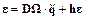 вектор
вектор 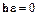 .
.
Добавив в соотношение (6) уравнение (5) получаем следующую систему уравнений с квадратной матрицей коэффициентов
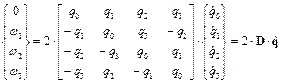 . (8)
. (8)
Используя свойство 1 можно показать, что для матрицы коэффициентов 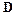 выполняется условие
выполняется условие
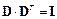 , (9)
, (9)
то есть ее обратная матрица равна транспонированной матрице 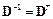 .
.
Разрешив систему уравнений (8) относительно  представим результат в следующем виде
представим результат в следующем виде
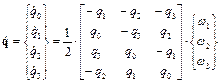 . (10)
. (10)
Обозначив 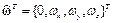 запишем (8) в следующем виде
запишем (8) в следующем виде
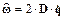 . (11)
. (11)
Используя (9) и (11) можно показать, что
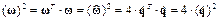 (12)
(12)
Продифференцировав (5) получаем следующее соотношение
 . (13)
. (13)
Добавив в соотношение (7) уравнение (13) получаем следующую систему уравнений с такой же квадратной матрицей коэффициентов 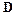 как и в системе уравнений (8)
как и в системе уравнений (8)
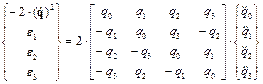 . (14)
. (14)
Разрешив систему уравнений (14) относительно 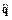 с учетом (12) представим результат в следующем виде
с учетом (12) представим результат в следующем виде
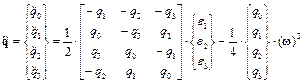 . (15)
. (15)
Для удобства представления итоговых соотношений введем следующие матрицы размером 4*3
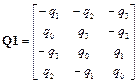 ;
;
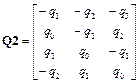 .
.
Подводя итоги можно констатировать, что угловые скорости и ускорения двух систем координат – базисов 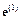 и
и  связаны с параметрами Эйлера следующими соотношениями
связаны с параметрами Эйлера следующими соотношениями
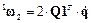 ;
;
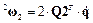 ;
;
 ;
;
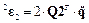 ;
;
 ;
;
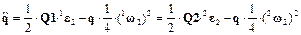 ,
,
где 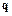 - параметры Эйлера, определяющие поворот базиса
- параметры Эйлера, определяющие поворот базиса  относительно базиса
относительно базиса 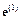 при их первоначальном совпадении;
при их первоначальном совпадении;
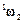 - угловая скорость базиса
- угловая скорость базиса  относительно базиса
относительно базиса 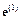 в системе координат базиса
в системе координат базиса 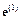 ;
;
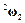 - угловая скорость базиса
- угловая скорость базиса  относительно базиса
относительно базиса 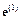 в системе координат базиса
в системе координат базиса  ;
;
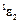 - угловое ускорение базиса
- угловое ускорение базиса  относительно базиса
относительно базиса 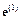 в системе координат базиса
в системе координат базиса 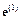 ;
;
 - угловое ускорение базиса
- угловое ускорение базиса  относительно базиса
относительно базиса 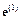 в системе координат базиса
в системе координат базиса  .
.
|